Практическое занятие
По выполнению преобразований в различных системах счисления,
Выполнению расчётов с логическими операциями
И решению задач программирования на условном языке или с помощью блок-схем.
Преобразования чисел в различных системах счисления.
1.1. Общие вопросы.
Наиболее простой и понятной нам системой счисления является десятичная (десятеричная). На самом деле она ничем не отличается от остальных систем по сложности выполнения расчётов, просто мы к ней привыкли. Тем не менее, эта система счисления является основной для большинства людей и наиболее распространенной по всему миру. Десятичная система счисления относится к так называемым позиционным системам счисления – это системы, в которых значение числа зависит не только от символа (символов), которыми число отображается, но и от позиции этого символа (этих символов) в числе.
Однако для вычислительной техники предпочтительнее использовать двоичную систему счисления, так как информация в компьютере представлена в виде электрических сигналов, которые имеют всего два варианта существования: либо электрический сигнал есть – обозначается 1, либо электрического сигнала нет – обозначается 0. Кроме этого для компактной записи информации в компьютере используется шестнадцатиричная система счисления, которая позволяет меньшим количеством символов записать большее количество информации.
Наряду с этими системами могут существовать и восьмеричная, и семеричная, и любая другая система счисления. Если понять принцип организации этих систем, то нет никакой разницы, в какой из систем представлено число, и можно довольно просто произвести преобразование числа из одной системы в другую.
1.2. Двоичная система счисления
Для понимания принципов работы в двоичной системе, как правило, ограничиваются 1 байтом, т.е. двоичным числом, состоящим из 8 разрядов. Такое число позволяет выполнять операции в пределах десятичного числа 255 (25510 – для обозначения системы используется подстрочный индекс).
Рассмотрим структуру одного байта с точки зрения десятичной системы:
| 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | Степень числа 2 при наличии значения в разряде |
| Значение разряда (если значение равно нулю, то и результат тоже равен нулю) | ||||||||
| Результат при значении разряда, равного единице, равен числу 2, возведённому в степень указанную в верхней строке |
Суммируя все результаты нижней строки, получаем: 128+64+32+16+8+4+2+1=255.
Если наше число больше, то используются дополнительные разряды, дописываемые слева. Так, например, оперируя 2 байтами, можно работать с десятичными числами в пределах 65 535.
Для решения задачи пересчёта двоичной системы в десятичную существует много вариантов, и можно использовать любой, однако, нам кажется, нагляднее и удобнее следующий вариант:
Перевести двоичное число 100110102 в десятичное. Для этого подставим данное число в приведённую выше таблицу в средний ряд (Значение разрядов). Соответственно в нижнем ряду получим следующие значения и просуммируем их.
Стандартная таблица для пересчета:
| 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
Подставляем в средний ряд вместо единиц наше число 100110102 и получаем следующие значения (если значение разряда равно нулю, следовательно, значение в ячейке нижнего ряда также равно нулю):
Складываем: 128+16+8+2=144.
Обратный перевод: число 23510 перевести в двоичную систему. Логика решения задачи следующая: 1) число 235 не больше 255, следовательно, для записи его в двоичной системе одного байта будет достаточно; 2) смотрим, какое максимальное число из нижнего ряда таблицы не превышает данное (естественно, 128); 3) вычитаем 128 из 235 и в значении разряда этого числа в среднем столбике ставим 1 (если это число не помещается в наше, то ставиться 0);
4) далее анализируем остаток (107), от остатка отнимаем следующее число (64), помещающееся в остаток и в разряде этого числа ставим 1, и т.д. Итак, число 235 равно:
Шаги 2 и 3: 235-128=107 – ставим 1 в разряде, соответствующем 128
Шаг 4: 107-64=43 – ставим 1 в разряде, соответствующем 64; далее повторяем процедуру 4), пока не останется ноль:
43-32=11 - ставим 1 в разряде, соответствующем 32,
11- 16 – не отнимается, ставим 0 в разряде, соответствующем 16,
11-8 = 3- ставим 1 в разряде, соответствующем 8,
3 – 4 – не отнимается, ставим 0 в разряде, соответствующем 4,
3-2 = 1 - ставим 1 в разряде соответствующем 2,
1-1 = 0 - ставим 1 в разряде соответствующем 1.
Сводим все в таблицу:
Проверяем: 128+64+32+8+2+1=235
Получилось двоичное число: 111010112
Может это и не самый удобный способ, зато простой наглядный и надёжный.
Если десятичное число достаточно большое, то можно применить следующий вид записи:
Пример перевода по общепринятой методике (перевести в двоичное десятичное число 218):
| Число | ||||||||
| Делитель | ||||||||
| Остаток |

Соберем остатки от деления в направлении, указанной стрелкой, начиная с последней единицы, и получим число в двоичной системе счисления: 21810 = 110110102
Сложение и вычитание двоичных чисел производится по стандартной классической схеме, например:
Сложение Вычитание
+ 0 1 1 0 1 1 1 0
0 0 1 1 1 0 0 1
 1 0 1 0 0 1 1 1 1 0 1 0 0 1 1 1
| - 1 0 1 0 1 1 1 0
 0 1 1 0 0 0 1 0
0 1 0 0 1 1 0 0 0 1 1 0 0 0 1 0
0 1 0 0 1 1 0 0
|
При сложении двоичных чисел сумма в каждом разряде не может быть больше 2, если число получается равным двум, то в разряде записывается 0, а 1 переходит в следующий разряд. Если получается больше 2 (например, складывали три числа, все равны 1, получилось 3), то в данном разряде записывается остаток от вычитания из получившегося числа двойки (в нашем примере из трех вычесть 2, записываем 1), а 1 переходит в следующий разряд.
Примеры для повторения №1:
1. 22710 преобразовать в двоичную систему
2. 011010112 преобразовать в десятичную систему
3. 110112 -101112 = ответ в десятичной системе.
1.3. Шестнадцатеричная система счисления
Это позиционная система счисления, в которой значения символа может принимать 16 вариантов:
| № п/п | ||||||||||||||||
| значение | A | B | C | D | E | F |
Для записи 1 байта в шестнадцатеричной системе достаточно двух разрядов и максимальное шестнадцатеричное число, записанное 1 байтом равно – FF.
Пересчёт шестнадцатеричной системы в двоичную удобнее выполнять через ту же таблицу значений разрядов, что и при переводе двоичной системы в десятичную:
Первый шестнадцатеричный символ кодирует первые 4 разряда байта, а второй вторые 4 разряда, таким образом, байт можно поделить пополам и представить в следующем виде:
| Значение двоичного разряда | ||||||||
| Пересчёт в десятичную систему | ||||||||
| Пересчёт в шестнадцатеричную систему | ||||||||
| 8+4+2+1=15=F | 8+4+2+1=15=F | Значение шестнадцатеричного разряда (FF16) |
Таким образом, мы можем довольно легко и наглядно записать любое десятичное число в шестнадцатеричной, двоичной и десятичной форме, например, E916 разделим на 2 части (Е в шестнадцатеричной и 9 в шестнадцатеричной). Смотрим по таблице: E соответствует 14, а 9 соответствует 9, запишем это: Е16=1410 и 916=910
Теперь запишем десятичные числа 14 и 9 в двоичной системе:
| E16=8+4+2=1410=11102 | 916=8+1=910=10012 |
Теперь добавляем стандартную таблицу для перерасчета и находим десятичное число:
| 128+64+32+8+1=23310 |
Таким образом: E916→111010012→23310
Примеры для повторения №2:
2.1. 13710→шестнадцатеричную→двоичную
2.2. 100101112→шестнадцатеричную→десятичную
2.3. CA16→двоичную→десятичную
1.4. Восьмеричная система счисления
Также является позиционной системой счисления с основанием, равным 8.
Для пересчёта восьмеричной системы в десятичную, используем стандартный, классический вариант. Суть его заключается в том, что для перевода чисел из любой системы счисления в десятичную можно использовать следующую схему:
A*Xk, где
А – значение числа в разряде,
Х – значение основания системы счисления,
K – значение позиции разряда
Например, если число четырехзначное в восьмеричной системе, то его перевод будет выглядеть так:
А4*83+ А3*82+ А2*81+ А1*80
например:
3778→десятичную =3*82+7*81+7*80= 192+56+7=25510
Обратный перевод немного более сложный (так как уже сложно выполнять вычисления «в уме» - см. стандартную таблицу), но также выполним с помощью простого подбора, если речь идёт о небольших числах, будем исходить максимум из трёхзначного числа в восьмеричной системе, например:
24110→ восьмеричную.
Предполагаем, что более трёх разрядов в восьмеричной системе для обозначения этого числа не понадобиться, третий разряд в восьмеричной системе равен значению числа А*82=А*64. Считаем, сколько раз по 64 может уложиться в 24110 целиком, получается 3*64=192. Таким образом, значение первого разряда числа 24110 в восьмеричной системе будет равно 3. Находим остаток для определения второго разряда восьмиричной системы: 241-192=49. Смотрим, сколько раз по 81=8 может поместиться в 49, получается 6*8=48, таким образом, значение второго разряда восьмеричной системы будет равно 6. У нас осталось значение первого разряда восьмиричной системы, равное 49-48=1. Таким образом: 24110→3618
Стандартная таблица для пересчета (подбора) в восьмеричной системе:
| 87 | 86 | 85 | 84 | 83 | 82 | 81 | 80 |
| 2 097 152 | 262 144 | 32 768 | 4 096 |
Сложение и вычитание в восьмеричной системе также выполняются по классическим правилам, например:
| Сложение | Вычитание |
+2 3 48
1 6 78
 4 2 38 4 2 38
| - 2 3 48
1 6 78
 4 58 4 58
|
При сложении восьмеричных чисел сумма в каждом разряде не может быть больше 8, если число получается равным восьми, то в разряде записывается 0, а 1 переходит в следующий разряд, если больше 8, то в данном разряде записывается остаток от вычитания из получившегося числа 8, а 1 переходит в следующий разряд.
Рассмотрим приведённый выше пример: складываем последние разряды 4+7=11, значит, в последнем разряде будет записано 11-8=3, а 1 переходит в старший разряд. Складываем вторые разряды: 1 (перешло из предыдущего разряда)+3+6=10, значит, во втором разряде запишем 10-8=2, и 1 переходит в старший разряд. И в третьем разряде запишем: 1(перешло из предыдущего разряда)+2+1=4. Таким образом, результат = 4238.
Вычитание выполняется аналогичным образом. Из 4 вычесть 7 нельзя. Берём 1 из старшего разряда и получаем в последнем разряде значение 8+4=12. Из 12-7=5, таким образом, значение последнего разряда равно 5. В старшем разряде осталось значение 3-1(заимствованное значение) =2. Из 2 вычесть 6 нельзя. Повторяем процедуру аналогичную для первого разряда: 8+2=10 и из 10-6=4, таким образом, во втором разряде будет число 4. В старшем разряде остаётся: 2-1(заимствованный разряд)=1, вычитаем 1-1=0. Результат: 458
Примеры для повторения №3:
3.1. 21810→восьмеричную→семеричную
3.2. 2558→десятичную→шестнадцатеричную
3.3. 011011112→восьмеричную
3.4. 1678+2558
3.5. 4558-2678
Коварные вопросы по системам счисления:
1. Сколько вариантов комбинаций можно закодировать 1 байтом?
2. Какое максимальное десятичное число можно записать 1 байтом?
3. Если десятичное число чётное, то в двоичной системе последним будет 0 или 1?
4. Какому разряду в двоичной системе соответствует 25?
5. Чему будет равно максимальное десятичное число, записанное одним байтом в шестнадцатеричной системе?
6. Чему будет равно десятичное число 256 в шестнадцатеричной системе?
7. Какое значение примет число последнего разряда, если в нём складываются 5 и 7 в восьмеричной системе?
Логические операции.
В основе работы вычислительной техники лежат логические операции, выполняемые над двоичными значениями. Это связано с тем, что электронные устройства (логические микросхемы) обрабатывают электрические сигналы, которые либо существуют – логическое обозначение - «1», либо не существуют - логическое обозначение - «0». В качестве основных выделяют три логические операции:
1. Логическое отрицание – «NOT» или «НЕ», либо знак отрицания « » или
» или  (чёрточка вверху обозначает – «НЕ» X)
(чёрточка вверху обозначает – «НЕ» X)
2. Логическое умножение или конъюнкция – «AND» или «И», либо знак конъюнкции «^». В языках программирования также могут встречаться следующие обозначения: А && В, А & В, А · В, А AND В
3. Логическое сложение или дизъюнкция – «OR» или «ИЛИ», либо знак дизъюнкции «˅». В языках программирования также могут встречаться следующие обозначения: А||В, А|В, А+В, А OR В
Логическая операция отрицания унарная, т.е. может выполняться над одним значением. А логические операции конъюнкции и дизъюнкции бинарные, т.е. для их выполнения необходимо как минимум 2 значения.
Суть логических операций (функций) следующая:
1. Функция отрицания «НЕ» возвращает противоположное значение исходного числа, например: если А=1, то 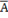 =0 и наоборот: если А=0, то
=0 и наоборот: если А=0, то 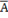 =1. Двойное отрицание числа
=1. Двойное отрицание числа 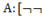 А], возвращает само число А.
А], возвращает само число А.
2. Функция конъюнкции «И» принимает значение 1, если и только тогда, когда все переменные (или обе переменные) равны 1, (и, соответственно, равна 0, если хотя бы одна из этих переменных равна 0), например: если А=1, В=1, то А ˄ В=1; если А=1, а В=0, то А ˄ В=0, а также если А=0, а В=0, то А ˄ В=0
3. Функция дизъюнкции «ИЛИ» принимает значение 1, если хотя бы одна переменная (как минимум из двух) равна 1, (и, соответственно, равна 0, если все переменные равны 0), например: если А=1, В=1, то А ˅ В=1; также А=1, В=0, то А ˅ В=1, и только если А=0, В=0, то А ˅ В=0
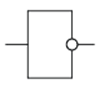
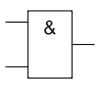
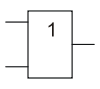
Графическое обозначение логических операций:
| Отрицание (инвертор) | Умножение (конъюнкция) | Сложение (дизъюнкция) |
| 
| 
|
Таблица истинности.
Основные операции можно представить в единой таблице, которую чаще всего называют таблицей истинности:
| X | Y | not X | XandY | XorY | XxorY |
(XxorY– логическая операция, исключающая ИЛИ, фактически проверяет на соответствие два значения, если они равны, то возвращается 0, если не равны, то возвращается 1).
Примеры выполнения расчётов с логическими операциями.
Логическое умножение одного байта на другой выполняется побитно, например:
| X= | 010111012 |
| Y= | 001101012 |
| X AND Y | 000101012 |
Аналогично выполняется и логическое сложение:
| X= | 010111012 |
| Y= | 001101012 |
| X OR Y | 011111012 |
Пример 1.
Решения задачи следующего вида: ( ˄ В)˅(А ˄ В)
˄ В)˅(А ˄ В)
| А | В | 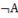
|  ˄ В ˄ В
| А ˄ В | ( ˄ В)˅(А ˄ В) ˄ В)˅(А ˄ В)
|
Данный пример решается следующим образом:
Вначале, исходя из приоритета логических операций, находится значение 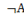 , затем находится значение
, затем находится значение  ˄ В, затем находится значения А ˄ В и на последнем этапе определяется значение (
˄ В, затем находится значения А ˄ В и на последнем этапе определяется значение ( ˄ В)˅(А ˄ В). Таким образом мы нашли ответы для заданного примера для всех возможных исходных вариантов А и В.
˄ В)˅(А ˄ В). Таким образом мы нашли ответы для заданного примера для всех возможных исходных вариантов А и В.
Пример 2.
Заданы логические выражения:
a. x<y OR x<z
b. x<y AND y<z
c. y>x AND z>x
Если число x имеет минимальное значение среди попарно неравных трёх чисел x,y и z, то значение ИСТИНА принимают выражения?
Выражение [а.] будет истинно так как x<y и x<z т.е. обе части уравнения будут истины.
Выражение [b.] может быть как истинным, так и ложным, так как x<y, а вот у<z мы не знаем, а уравнение будет истинным, если обе части будут истинными.
Выражение [с.] будет истинным, так как и y и z больше x, т.е. обе части уравнения будут истинными, и в результате получим истину.
Таким образом, ответ будет: a,c
Примеры для повторения №4:
1. с=а ˄в; а= 11011011 и в=00111010, чему будет равно с?
2. (А ˅ В) ˄ (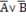 ), если А=1, а В=0
), если А=1, а В=0
3.
| А | В | (НЕ А ИЛИ НЕ В) И А |