Протокол измерений к лабораторной работе № 7

Теоретическая справка

В электрических цепях, как правило, в качестве критерия режима резонанса принимают условие совпадения по фазе тока и напряжения в пассивных двухполюсниках, содержащих индуктивные, емкостные и резистивные элементы. Рассмотрим последовательное соединение резистивного, индуктивного и емкостного элементов (R L C – контур).

Пусть напряжение на входе – синусоидальное , частота w может меняться в пределах от нуля до ¥.

 

Составим уравнение для контура:

, , , .

Применим комплексный метод расчета. Комплексная схема замещения и векторные диаграммы комплексных напряжений на заданной частоте (, ) имеют вид:

 

При характер цепи – индуктивный (ток отстает от напряжения); при – емкостной (ток опережает напряжение); при – резистивный, т.е. ток совпадает по фазе с напряжением. В таком случае цепь настроена в резонанс, а на участке (b d) наблюдается резонанс напряжений.

 

Действительно, если , то

и .

Тогда . Входное сопротивление цепи

– чисто активное.

Из условия следует, что резонанса можно достичь, изменяя частоту напряжения источника или параметры реактивных элементов – индуктивность и емкость. Угловая частота, при которой наступает резонанс, называется резонансной угловой частотой: и . Индуктивное и емкостное сопротивление при резонансной частоте равны . Величина ρ называется характеристическим сопротивлением цепи или контура. Напряжения на индуктивности и емкости при резонансе равны и могут значительно превышать входное напряжение, которое равно напряжению на активном сопротивлении. Отношение напряжения на индуктивности или емкости к входному напряжению при резонансе называют добротностью контура:

.

 

В общем случае комплексное входное сопротивление зависит от частоты и параметров элементов:

,

модуль комплексного входного сопротивления , угол комплексного входного сопротивления .

В теоретическом случае при R =0 полное сопротивление цепи при резонансе равно нулю, а ток в контуре и напряжения на реактивных элементах бесконечно велики. При R ≠0 полное сопротивление при минимально, а ток максимален и равен .

Зависимости действующего (или амплитудного) значения тока, напряжений на элементах , , и от частоты приложенного напряжения называют резонансными кривыми. Зависимость параметров цепи , , от частоты приложенного напряжения называют частотными характеристиками. Действующее значение входного напряжения при этом .

Резонансные кривые тока и напряжения также строят в относительных единицах; для разных значений добротности контура кривые имеют вид:

 

Резонансные кривые напряжений:

 

 

 

Замечание: Для цепи с добротностью возрастание U_L от нуля до значения U происходит монотонно, а для цепи с добротностью напряжение U_L при некоторой частоте достигает максимального значения U_{L max}> U, а затем уменьшается до значения U. Для цепи с добротностью напряжение U_С монотонно убывает от U до нуля, а для цепи с добротностью напряжение U_С при некоторой частоте достигает максимального значения U_{C max} > U, а затем уменьшается до нуля.

 

Частотные характеристики последовательного контура:

 

Резонансные кривые и частотные характеристики показывают, что цепь обладает избирательными свойствами: обладает наименьшим сопротивлением для тока той частоты, которая наиболее близка к резонансной. Избирательные свойства широко используются в электротехнике и радиотехнике. При этом режим резонанса является нормальным режимом работы устройства. Наоборот, в устройствах, где резонансный режим не предусмотрен, значительные токи и напряжения могут быть опасными. Для оценки избирательных свойств цепи вводят условное понятие ширины резонансной кривой или полосы пропускания контура, которую определяют как разность частот, между которыми ток превышает значение (). Пересечение горизонтальной линии () с резонансными кривыми определяет граничные частоты w₁ и w₂, между которыми расположена полоса пропускания.

Чем выше добротность, тем уже полоса пропускания: . Модуль комплексного сопротивления цепи

Действующее значение тока .

 

 

Подготовка к работе

1. Начертить схему последовательного RLC контура – последовательно соединенных катушки L_a с параметрами (R _к, L), конденсатора C и резистора R. Значения емкости конденсатора представлены в табл. 1, для катушки L_a индуктивность L =0,13 Гн, сопротивление резистора R =10 Ом. Вычислить резонансную частоту , характеристическое сопротивление контура ρ. Записать аналитические выражения для определения добротности контура , граничных частот и , ширины резонансной кривой (полосы пропускания) с учетом сопротивления проводов катушки . Объяснить как, используя показания приборов в режиме резонанса, определить сопротивление проводов катушки .

2. Как изменится добротность контура и ширина резонансной кривой, если сопротивление резистора R увеличить в 2 раза?

3. Записать аналитические выражения резонансных кривых , , , (при неизменном действующем значении напряжения U на входе); частотных характеристик , , где — модуль входного сопротивления контура, .

4. Построить качественно:

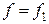а) частотные характеристики , , отметить значения и при частотах , и ;

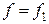б) в одной координатной плоскости резонансные кривые , , ,отметить значения при частотах , и .

5. Построить качественно векторно-топографические диаграммы для частот , , .

 

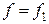Таблица 1

N
С, мкФ						47; 47 последовательно
N
С, мкФ	56; 56 последовательно	68; 68 последовательно	82; 82 последовательно	22; 22 параллельно	33; 33 параллельно	33; 47 параллельно

Содержание и порядок выполнения работы

Схема исследуемой цепи представлена на рис. 1П. Источником синусоидального напряжения является модуль ФУНКЦИОНАЛЬНЫЙ ГЕНЕРАТОР. В работе используют измерительные приборы из блоков ИЗМЕРИТЕЛЬ ФАЗЫ и МОДУЛЬ МУЛЬТИМЕТРОВ.

 

· Собрать электрическую цепь по схеме, приведенной на рис. 1П протокола измерений. Тумблер SA2 модуля ИЗМЕРИТЕЛЬ ФАЗЫ установить в положение I2. Резистор R выбрать из МОДУЛЯ СОПРОТИВЛЕНИЙ R =10 Ом.

· Проверить собранную электрическую цепь в присутствии преподавателя.

· Включить автоматический выключатель QF блока модуль питания и тумблер Сеть модуля ФУНКЦИОНАЛЬНЫЙ ГЕНЕРАТОР. Переключатель Форма установить в положение . Установить регулятором Частота значение частоты Гц.

· Регулятором Амплитуда модуля ФУНКЦИОНАЛЬНЫЙ ГЕНЕРАТОР установить действующее значение напряжения U = 3–5 В.

· Плавно меняя частоту генератора, модулем ИЗМЕРИТЕЛЬ ФАЗЫ измерить действующее значение напряжения u, тока i; угол сдвига фаз j. Напряжение U поддерживать в работе неизменным. Заполнить таблицу 1П: записать значения частоты и действующего значения тока, при котором j=0 (резонанс), j=±45° (граничные частоты). Провести необходимые вычисления. Данные занести в Таблицу 1П.

· Повторить опыт, увеличив сопротивление резистора R в 2 раза (последовательное включение двух резисторов R =10 Ом). Данные занести в Таблицу 1П.

· Рассчитать сопротивление проводов катушки (Таблица 2П).

· Рассчитать при R =10 Ом или R =20 Ом по формулам п.1 Подготовки к работе характеристическое сопротивление контура ρ, добротность контура , граничные частоты и , ширину резонансной кривой (полосы пропускания) с учетом сопротивления проводов катушки .

· Сравнить опытные и расчетные данные (Таблица 3П).

· Установить R =10 Ом или R =20 Ом.

· Плавно изменяя частоту в пределах от до , выполнить измерения действующих значений напряжения на катушке и конденсаторе мультиметрами РР, действующее значение тока , угла сдвига фаз между напряжением и током на входе модулем ИЗМЕРИТЕЛЬ ФАЗЫ. Измеренные значения занести в Таблицу 4П.

· Построить в масштабе на миллиметровой бумаге частотные характеристики и резонансные кривые по аналитическим выражениям п.3 Подготовки к работе. Нанести опытные данные на построенные частотные характеристики и резонансные кривые, проанализировать полученный результат.

· Выключить тумблер Сеть модуля ФУНКЦИОНАЛЬНЫЙ ГЕНЕРАТОР и автоматический выключатель QF модуля питания.

 

 

Протокол измерений к лабораторной работе № 7

«Исследование резонанса в цепи
с последовательно соединенными элементами R, L, C »

Схема исследуемой электрической цепи представлена на рис. 1П.

Рис. 1П

Параметры элементов цепи: L =0,13 Гн; С = мкФ.

Экспериментальные данные при U = B занесены в табл. 1П.

 

Таблица 1П.

R =10 Ом теоретический расчет: f 0 =_______ Гц
j=0	f 0 = Гц	I 0= мА
j=-45°	f 1 = Гц	I 1= мА
j=+45°	f 2 = Гц	I 2= мА
R =20 Ом теоретический расчет: f 0 =_______ Гц
j=0	f 0 = Гц	I 0= мА
j=-45°	f 1 = Гц	I 1= мА
j=+45°	f 2 = Гц	I 2= мА

 

Таблица 2П

R =10 Ом	U = B I 0= мА	= Ом
R =20 Ом	U = B I 0= мА	= Ом
= Ом

 

Таблица 3П

R = Ом, = Ом	Теоретический расчет	Эксперимент (Таблица1П)
f 0
f 1, f 2
ρ
Q

 

 

Экспериментальные данные при U = B, R = Ом занесены в табл. 4П.

 

= _______ Ом.

Таблица 4П

, Гц			f 1		f 0		f 2
I, мА
, град
, В
, В
, В

 

Содержание отчета

Заполнить табл. 3П, провести проверку результатов теоретического расчета и экспериментальных данных. Построить теоретические зависимости частотных характеристик и резонансных кривых. Сравнить теоретические зависимости с экспериментальными. Построить векторные диаграммы тока и напряжений при резонансной и граничных частотах.

 

5. Контрольные вопросы

1. По каким из резонансных характеристик следует определять добротность и ширину резонансной кривой?

2. В последовательном RLC контуре при резонансе известны приложенное напряжение U, напряжение на катуш­ке и напряжение на конденсаторе . Почему добротность цепи, определенная как и получается различной? В каком случае она больше?

3. Как доказать равенство 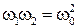, где , и — граничные частоты полосы пропускания и резонансная час­тота последовательного RLC контура?

4. Как влияет на добротность и ширину резонансной кривой изменение резистивного сопротивления последовательного RLC контура? Сравните данные теоретического расчета и экспериментальные данные Таблицы 1П. Объясните расхождение данных.

5. Построить зависимости , , , (при неизменном действующем значении напряжения U и частоте f = f ₀).

6. Построить зависимости , , , (при неизменном действующем значении напряжения U и частоте f = f ₀).