Понятие о напряжениях в точке бруса.
Наряду с понятиями деформации одним из основных понятий сопротивления материалов является напряжение.
Напряжением называют меру воздействия внутренних силовых факторов на единицу площади в рассматриваемой точке сечения бруса.
Напряжение характеризует интенсивность внутренних сил, действующих в сечении.
Полное напряжение – часть внутренних усилий, приходящаяся на конкретную точку сечения.
Рассмотрим какой-либо произвольно нагруженный брус и применим к нему метод сечений т.е рассечем тело произвольным сечением.
Введем правую систему координат. Ось z направим перпендикулярно проведенной плоскости.
Выделим в этом сечении бесконечно малый элемент.
Площадь элементарной площадки обозначим dА.
Ввиду малости этого элемента можно считать, что в его пределах внутренние силы, приложенные в различных точках, одинаковы по модулю и направлению, и следовательно, представляют собой систему параллельных сил. Равнодействующую этой системы обозначим dR.
Разделив dR на площадь элементарной площадки dА определим интенсивность внутренних сил, т.е. напряжение р в точках элементарной площадки dА.
т.о. напряжение есть внутренняя сила, отнесенная к единицы площади сечения. Напряжение величина векторная.
Единицы измерения
Поскольку эта единица напряжения очень мала, то мы будем применять более крупную кратную единицу
В общем случае вектор полного напряжения в точке может располагаться под любым углом к сечению. В таких случаях для существенного упрощения расчетов его удобно раскладывать на составляющие (проекции):
Разложим вектор напряжения на две составляющие:
- нормальное напряжение, перпендикулярно плоскости сечения (параллельно оси z, параллельно нормали) характеризует интенсивность сил отрыва или сжатия частиц элементов конструкции;
– полное касательное напряжение, лежащее в плоскости сечения, характеризует интенсивность сил, сдвигающих эти части в плоскости сечения. Его разложим на две составляющие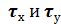 
,
Введем индексы.
Первый индекс говорит о том, какой оси параллельна нормаль. Так как в примере мы рассмотрели нормаль параллельную оси z, следовательно, индекс у нормального напряжения будет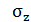 
, у касательных напряжений будет два индекса. Первый показывает, какой оси сечение перпендикулярно, второй, какой оси данное касательное напряжение параллельно 
и 
.
Через точку А можно провести нормальное сечение к оси у и х и получить еще два сечения в которых по нормали будет направлено нормальное напряжение и еще два касательных.
Так как у нас три грани, мы получаем в точке А 9 компонентов напряжений, которые дают полное представление о деформированном состоянии точки твердого тела.
Для того, чтобы вычислить значение полного напряжения мы воспользуемся теоремой Пифагора, так как диагональ параллелепипеда определяется суммой квадратов сторон.
Вывод:
В нагруженном теле в каждой точке сечения в общем случае возникают нормальное напряжение 
, направленное перпендикулярно к сечению, и касательное 
, лежащее в плоскости сечения.
Как известно, через точку можно провести бесконечное количество плоскостей и в этой точке будут напряжения и , перпендикулярные и лежащие в этих плоскостях.
Таким образом, напряженное состояние в точке можно представить совокупностью всех и , возникающих в ней.
Для характеристики напряженного состояния в точке достаточно знать значения нормальных и касательных напряжений на трех взаимно перпендикулярных площадках.
Их удобнее представить в виде параллелепипеда с бесконечно малыми гранями. Поскольку расстояние между гранями бесконечно мало, то можно считать, что на противоположных гранях параллелепипеда возникают одинаковые по величине напряжения, но направленные противоположно.
Напряженным состоянием тела в точке называют совокупность нормальных и касательных напряжений, действующих по трем взаимно перпендикулярным площадкам (сечениям), содержащим данную точку.
4.Зависимости между напряжениями и внутренними силовыми факторами.
Из рассмотренного выше материала можно сделать вывод, что внутренние силы классифицируются - на распределенные и сосредоточенные. Распределенные представляют собой напряжения, а сосредоточенные ВСФ.