Аппроксимация характеристик нелинейных элементов
Методы аппроксимации
Как правило, ВАХ нелинейных элементов 
получают экспериментально, поэтому чаще всего они заданы в виде таблиц или графиков. Чтобы иметь дело с аналитическими выражениями, приходится прибегать к аппроксимации.
Методы аппроксимации, используемые в линейных цепях, могут быть использованы и для представления характеристик нелинейных цепей. Отличие будет состоять в выборе аналитических зависимостей, так как аппроксимации подлежат функции совершенно другого класса (в частности, ВАХ, а не АЧХ, ФЧХ и временные).
Обозначим заданную таблично или графически ВАХ нелинейного элемента 
, а аналитическую функцию, аппроксимирующую заданную характеристику, 
, где ― коэффициенты этой функции, которые нужно найти в результате аппроксимации.
В методе Чебышева коэффициенты 
функции 
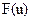находятся из условия
, (1)
т.е. они определяются в процессе минимизации максимального уклонения аналитической функции от заданной. Здесь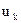 
, 
― выбранные значения напряжения.
При среднеквадратичном приближении коэффициенты должны быть такими, чтобы минимизировать величину
. (2)
Приближение функции по Тейлору основано на представлении функции рядом Тейлора в окрестности точки 
(3)
и определении коэффициентов этого разложения. Если ограничится первыми двумя членами разложения в ряд Тейлора, то, очевидно, речь пойдет о замене сложной нелинейной зависимости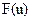 
более простой линейной зависимостью. Такая замена называется линеаризацией характеристик.
Заметим, что первый член разложения (3) 
представляет собой постоянный ток в рабочей точке при , второй член 
– дифференциальную крутизну вольтамперной характеристики в рабочей точке, т.е. при
Наиболее распространенным способом приближения заданной характеристики является интерполяция (метод выбранных точек), при которой коэффициенты аппроксимирующей функции 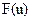находятся из равенства этой функции и заданной 
в выбранных точках (узлах интерполяции) 
Таким образом, задача аппроксимации ВАХ нелинейных элементов заключается в выборе вида аппроксимирующей функции и определения ее коэффициентов одним из указанных выше методов.
Степенная (полиномиальная) аппроксимация
Такое название получила аппроксимация ВАХ степенными полиномами
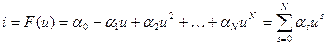. (4)
Иногда бывает удобно решать задачу аппроксимации заданной характеристики в окрестности точки 
, называемой рабочей. Тогда используют степенной полином.
. (5)
Определить коэффициенты полинома (4) можно различными способами. При среднеквадратичном приближении они находятся из условия 
, где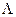 
определяется формулой (2).
Из математики известно, что минимум функции нескольких переменных достигается при равенстве нулю производных функции по ее параметрам, т.е. при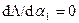 
, 
. Если подставить в формулу (2) выражение степенного полинома, вычислить производные
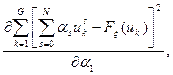l=0, 1,…, N,
И приравнять их к нулю, то получим, что коэффициенты , дающие наилучшее среднеквадратичное приближение, находятся из решения следующей линейной системы уравнений:
, 
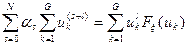. (6)
При этом число точек u=uk, в которых оценивается приближение, может быть гораздо больше числа коэффициентов .
Применение метода интерполяции (метода выбранных точек), когда добиваются совпадения 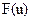и в выбранных точках u=uk, приводит к линейной системе уравнений
, 
, (7)
Из которой и находятся коэффициенты . В этом методе число выбранных точек (узлов интерполяции) 
должно совпадать с числом коэффициентов.
Существуют также способы определения коэффициентов степенного полинома путем минимизации чебышевской погрешности (1), использования разложения в ряд Тейлора и др. Степенная аппроксимация широко используется при анализе работы нелинейных устройств, на которые подаются относительно малые внешние воздействия, поэтому требуется достаточно точное воздействие нелинейности характеристики в окрестности рабочей точки.
Пример. На рис 4 кружочками показана полученная экспериментально характеристика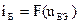 
, т.е. зависимость тока базы от напряжения между базой и эмиттером для транзистора КТ301. Осуществим постепенную аппроксимацию этой характеристики в диапазоне 
от 0,4 до 0,9 В полиномом второй степени в окрестности рабочей точки 
.
Коэффициенты 
, 
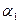, и 
полинома 
найдем, используя метод интерполяции. Выберем в качестве узлов интерполяции точки, соответствующие напряжениям 
, и составим систему уравнений (7):
Решение этой системы дает 
, 
, 
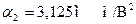. Кривая тока 
проходит через три экспериментальные точки, соответствующие узлам интерполяции (рисунок 4 кривая 1). Из рисунка видно, что некоторые экспериментальные точки (например, при 
) плохо «ложатся» на эту кривую. Кроме того, нас не устраивает изгиб в нижней части характеристики.
Более лучшей аппроксимации можно добиться, если использовать полином четвертой степени и выбрать соответственно пять узлов интерполяции (0,4; 0,5; 0,6; 0,7; 0,8; 0,9 В). В этом случае кривая тока пройдет через все пять экспериментальных точек.
Однако можно попытаться сохранить вторую степень полинома и улучшить аппроксимацию, воспользовавшись каким―либо другим методом для определения коэффициентов , , 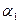и . Попробуем найти эти коэффициенты, используя среднеквадратическое приближение тока ко всем пяти экспериментальным значениям. Составим уравнения (6):
Решение этой системы уравнений α0 =0,164 мА, α1 =1,07 мА/В и α2 =2,069 мА/В2.
График тока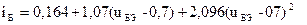 
показана на рисунке (кривая 2). Эта характеристика является, по―видимому, более приемлемой для аналитического описания экспериментальных результатов.
Рисунок 4― зависимость 
для транзистора КТ301
1.3 Кусочно―линейная аппроксимация
В тех случаях, когда на нелинейный элемент воздействуют напряжения с большими амплитудами, можно допустить более приближенную замену характеристики нелинейного элемента и использовать более простые аппроксимирующие функции. Наиболее часто при анализе работы нелинейного элемента в таком режиме реальная характеристика заменяется отрезками прямых линий с различными наклонами.
С математической точки зрения это означает, что на каждом заполняемом участке характеристики используются степенные полиномы (4) первой степени (
) с различными значениями коэффициентов 
и .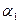
Пример. На рисунке 5 (кривая 1) проведен график экспериментальной зависимости 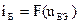транзистора КТ306. Выполним кусочно―линейную аппроксимацию этой зависимости.
Используя полином первой степени 
, осуществим аппроксимацию заданной зависимости в окрестности точки 
и определим коэффициенты по методу Тейлора (3):
Величина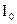 
― ток в рабочей точке ― в соответствии с экспериментальными данными равна 1,2 мА. Крутизну 
рабочей точке можно найти приближенно методом приращений:
.
 |
Рисунок 5― зависимость iБ=F(uБЭ) транзистораКТ306
В результате аппроксимации имеем
.
Видно, что при <0,5 B ток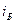 
принимает отрицательные значения, что не согласуется с экспериментальной зависимостью. Таким образом, полученный полином будет аппроксимировать заданную зависимость на участке >0,5. На участке же 
можно выбрать полином первой степени с нулевыми коэффициентами, т.е. 
. Итак, аппроксимирующая функция (рисунок 5, кривая 2) запишется в виде
Подобная аппроксимация применяется довольно часто, поэтому представим эту зависимость в более общей форме:
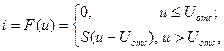
где напряжение 
называется напряжением отсечки.