ГЕТЕРОСКЕДАСТИЧНОСТЬ
Для нахождения оценок коэффициентов линейных регрессионных зависимостей обычно применяется метод наименьших квадратов (МНК). Для того, чтобы найти МНК-оценки коэффициентов линейной регрессии модели 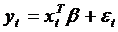 ,
, 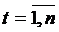 , достаточно, чтобы выполнялись условия теоремы Гаусса – Маркова:
, достаточно, чтобы выполнялись условия теоремы Гаусса – Маркова:
1. Eet=0, E(et2)=V(et)=s2 – не зависит от t, t=1…n.
2. E(etes)=0 при t ¹ s, некоррелированность ошибок для разных наблюдений.
3. Ошибки et, t=1…n, имеют совместное нормальное распределение: e~ 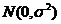 .
.
На практике часто встречаются задачи, в которых условия Гаусса – Маркова не выполняются. Следовательно, найденные с помощью МНК оценки неэффективные.
Тест на гетероскедастичность
Классическая модель с постоянными дисперсиями ошибок называется гомоскедастичной (3-е условие Гаусса – Маркова). Гетеро-скедастичной называется модель с некоррелированными, но имеющими непостоянную дисперсию ошибками. Для проверки модели на гетероскедастичность существует ряд тестов. Рассмотрим один из них.
Тест Голдфельда – Куандта:
Данный тест применяется в том случае, когда есть предположение о прямой зависимости дисперсии ошибки от величины некоторой независимой переменной (регрессора).
- Упорядочить данные по убыванию той независимой переменной, относительно которой есть подозрение на гетероскедастичность.
- Исключить d средних наблюдений (d=1/4 от общего количества наблюдений).
- Провести две независимые регрессии первых n/2–d/2 и последних n/2–d/2 наблюдений и построить соответствующие остатки e1 и e2.
- Составить статистику F=e’1e1/e’2e2, где 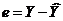 .
.
Если верна гипотеза Н0: s12 = s22 = …= sn2, то F имеет распределение Фишера с (n/2–d/2–k, n/2–d/2–k) степенями свободы. Большая величина этой статистики означает, что гипотезу Н0 надо отвергнуть.
|
|
В случае подтверждения гетероскедастичности для поиска оценок коэффициентов регрессии применяются следующие методы:
- обобщенный метод наименьших квадратов;
- доступный обобщенный метод наименьших квадратов в случаях, когда ошибка пропорциональна одной из независимых переменных или дисперсии ошибок принимают только 2 различных значения;
- обычный метод наименьших квадратов, если оценки ошибок представлены в форме Уайта или Невье – Веста.
Указания:
1. Так как для проведения теста Голдфельда – Куандта необходимо провести упорядочение данных, то используем MS EXCEL для этой процедуры. Скопируйте исходные данные из табл. 1 на рабочий лист MS EXCEL. Поставьте курсор на поле H2 и выберите в меню Данные / Сортировка… В появившемся окне Сортировка диапазона укажите: Сортировать по H2, по убыванию. Нажмите OK.
2. Исключим d средних наблюдений (d=20/4=5). Так как число наблюдений четное, то и d должно быть четное. Пусть d=6. Удалите с рабочего листа MS EXCEL шесть средних значений. Установите в ячейках с числами четыре десятичных знака после запятой, для этого выделите числовые данные и выберите в меню Формат / Ячейки.… В появившемся окне установите Числовой формат ячеек и число десятичных знаков – 4.
3. Создайте ряды для построения двух независимых регрессий первых n/2-d/2 и последних n/2-d/2 наблюдений. Пусть это будут ряды G1, V1, V2 и G2, S1, S2 соответственно. Скопируйте данные из рабочего листа MS EXCEL в группу Heterosked.
4. Оцените регрессию G1=a0+a1V1+a2V2+e методом наименьших квадратов, получим
G1=C(1)+C(2)*V1+C(3)*V2.
|
|
5. Создайте ряд для расчета остатков первой регрессии. Пусть это будет ряд E1. В строке формул введите
E1=G1-C(1)-C(2)*V1-C(3)*V2,
где С(1), С(2), С(3) – полученные оценки коэффициентов.
6. Повторите п.4 и п.5 для регрессии G2=a0+a1S1+a2S2+e. Ряд остатков назовите E2.
7. Создайте ряд для расчета F-статистики. Пусть это будет ряд F. В строке формул введите
Fрасчет=суммкв(E1^2)/суммкв(E2^2).
8. Создайте ряд для расчета критического значения F-статистики. Пусть это будет ряд F1. В строке формул введите
Fстат=Fраспобр(0,05;10-3-2;10-3-2).
(n/2–d/2–k, n/2–d/2–k)
N = 20, d=6, к=2
9.Сравните Fрасч и Fстат. Если Fрасчет<Fстат, то гипотеза о гетероскедастичности подтверждается, если Fрасч>Fстат, то отвергается. Сделайте соответствующие выводы.
Данные
| G | H1 | H2 |
| 8,2104 | 3,1888 | 0,8184 |
| 9,4664 | 3,5073 | 0,7825 |
| 4,1437 | 1,1118 | 0,4082 |
| 7,2167 | 2,7557 | 0,1757 |
| 6,4996 | 2,5607 | 0,6171 |
| 6,1195 | 1,6324 | 0,6175 |
| 8,0241 | 2,5668 | 0,5649 |
| 3,5661 | 1,1745 | 0,2279 |
| 5,1923 | 2,0434 | 0,0072 |
| 9,2843 | 3,4287 | 0,4699 |
| 4,8394 | 2,6283 | 0,1094 |
| 8,1565 | 2,5859 | 0,0701 |
| 8,6529 | 3,4448 | 0,2319 |
| 8,2597 | 3,4808 | 0,4129 |
| 6,4339 | 1,0466 | 0,6666 |
| 5,2972 | 1,2068 | 0,5232 |
| 9,2792 | 3,7045 | 0,3034 |
| 6,3919 | 1,6167 | 0,3289 |
| 5,4351 | 2,1220 | 0,6870 |
| 5,5254 | 2,1801 | 0,3986 |
В качестве задания можно предложить проверить наличие гетероскедастичности при предположении, что Н1 ее вызывает. То есть проделать аналогичную работу только для Н1.