Расчеты электрических цепей гармонического тока в тригонометрической форме или графически с помощью векторных диаграмм применяются на практике только в случае простых схем.
С усложнением электрических цепей, с увеличением числа контуров, источников энергии, добавлением взаимных индуктивностей и т. д. тригонометрические или графические расчеты становятся крайне затруднительными. Требуется метод, позволяющий рассчитывать электрические цепи переменного тока алгебраически, аналогично цепям постоянного тока. Таким удобным расчетным методом служит метод комплексных амплитуд (комплексный метод), введенный в электротехнику А. Е. Кеннеди и П. Ч. Штейнметцом в 1893 – 1894 гг. Этот метод, как и векторные диаграммы, основан на представлении гармонических функций в виде проекций вращающихся векторов, причем вращающиеся векторы выражаются аналитически, в комплексной форме. Алгебраически интерпретируя векторные диаграммы, этот метод удобно сочетает аналитические расчеты с геометрическими представлениями.
Все последующее изложение данного курса и радиотехнических дисциплин базируется на этом методе.
Известно, что каждая точка на комплексной плоскости определяется радиусом-вектором этой точки, т. е. вектором, начало которого совпадает с началом координат, а конец находится в точке, соответствующей заданному комплексному числу (рисунок 3.1).
Пользуясь показательной или полярной формой записи комплексного числа, имеем
.
Рисунок 3.1 Вектор, изображающий комплексное число
Здесь А – модуль;
a – аргумент;
(в электротехнике не пользуются обозначением 
, так как буква i обозначает ток).
Применив формулу Эйлера, можно получить тригонометрическую форму записи комплексного числа
|
|
или соответственно алгебраическую форму
,
где 
; 
.
Очевидно,
; 
.
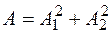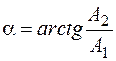Вектор, вращающийся в положительном направлении, т.е. против хода часовой стрелки, с угловой скоростью ω, может быть выражен следующим образом
, (3.1)
где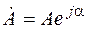 
(
– комплексная амплитуда, представляющая данный вектор в момент t = 0, рисунок 3.2). Иначе говоря, это комплексная величина, не зависящая от времени, модуль и аргумент которой равны соответственно амплитуде и начальной фазе заданной гармонической функции.
Множитель ej t является оператором вращения; умножение комплексной амплитуды на ej t означает поворот вектора наугол t в положительном направлении.
Записывая комплексную функцию (3.1) в тригонометрической форме
заключаем, что гармоническая функция Acos (w t +a) может рассматриваться как действительная часть комплексной функции (3.1), или, что то же, как проекция вращающегося вектора на действительную ось.
Условно это записывается так:
.
Символ Re обозначает, что берется действительная часть комплексной функции. Например,
,
где 
– комплексная амплитуда.
Аналогично функция Asin ( t +) может быть в случае необходимости представлена как мнимая часть комплексной функции (3.1), взятая без множителя j, или как проекция вращающегося вектора на мнимую ось.
Условно это записывается так
,
где символ Im обозначает, что берется мнимая часть комплексной функции. Например,
.
Другой способ представления гармонической функции с помощью комплексных величин основан на применении формул
|
|
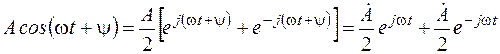; (3.2)
. (3.3)
Согласно (3.2) можно заключить, что функция Acos ( t +) равна геометрической сумме двух комплексно сопряженных векторов, имеющих модуль A /2 и вращающихся в противоположные стороны с одинаковой угловой скоростью ω.
В результате сложения таких двух векторов получается вектор, расположенный на действительной оси, т. е. для любого момента времени t получается действительная величина (рисунок 3.3, а).
Аналогично из (3.3) видно, что функция Asin (ω t +) равна геометрической разности тех же двух вращающихся векторов, деленной на j. Разность этих векторов для любого момента времени t представляет мнимую величину (рисунок 3.3, б), и поэтому ее делят на j для получения действительной функции.
а б
Рисунок 3.3 Представление гармонической функции
вращающимися комплексно-сопряженными векторами
Вращение вектора в отрицательном направлении (по ходу часовой стрелки) связано с понятием отрицательной круговой частоты (–), которое является чисто математическим понятием, вытекающим из вышеприведенных формул. Введение этого понятия в ряде случаев удобно для исследования процессов в электрических цепях. Из сравнения построения на рисунках 3.3, а и б, видно, что представление гармонических функций с помощью двух векторов, вращающихся в противоположные стороны, для функции вида Acos ( t +) проще, чем для функции Asin ( t +).