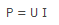Графические методы расчета
Графические методы расчета позволяют проводить анализ нелинейных цепей переменного тока для частных значений параметров с использованием характеристик нелинейных элементов для мгновенных значений, по первым гармоникам и действующим значениям
Графический метод с использованием характеристик для мгновенных значений
В общем случае методика анализа нелинейной цепи данным методом включает в себя следующие этапы:
-исходя из физических соображений находят (если он не задан) закон изменения одной из величин, определяющих характеристику нелинейного элемента;
-по нелинейной характеристике для известного закона изменения переменной путем графических построений определяют кривую (или наоборот);
-с использованием полученной зависимости проводят анализ остальной (линейной) части цепи.
Графический метод с использованием характеристик
для действующих значений (метод эквивалентных синусоид)
При анализе нелинейной цепи данным методом реальные несинусоидально изменяющиеся переменные заменяются эквивалентными им синусоидальными величинами, действующие значения которых равны действующим значениям исходных несинусоидальных переменных. Кроме того, активная мощность, определяемая с помощью эквивалентных синусоидальных величин, должна быть равна активной мощности в цепи с реальной (несинусоидальной) формой переменных. Используемый прием перехода к синусоидальным величинам определяет другое название метода - метод эквивалентных синусоид.
Строго говоря, характеристика нелинейного элемента для действующих значений зависит от формы переменных, определяющих эту характеристику. Однако в первом приближении, особенно при качественном анализе, этим фактом обычно пренебрегают, считая характеристику неизменной для различных форм переменных. Указанное ограничивает возможности применения метода для цепей, где высшие гармоники играют существенную роль, например, для цепей с резонансными явлениями на высших гармониках.
|
|
Переход к эквивалентным синусоидам позволяет использовать при анализе цепей векторные диаграммы. В связи с этим этапы расчета данным методом в общем случае совпадают с рассмотренными в предыдущем разделе.
Метод расчета с использованием характеристик для действующих значений широко применяется для исследования явлений в цепях, содержащих нелинейную катушку индуктивности и линейный конденсатор (феррорезонансных цепях), или цепях с линейной катушкой индуктивности и нелинейным конденсатором. Кроме того, данный метод применяется для анализа цепей с инерционными нелинейными элементами, у которых постоянная времени, характеризующая их инерционные свойства, много больше периода переменного напряжения (тока) источника питания. В этом случае в установившихся режимах инерционные нелинейные элементы можно рассматривать как линейные с постоянными параметрами (сопротивлением, индуктивностью, емкостью). При этом сами параметры определяются по характеристикам нелинейных элементов для действующих значений и для различных величин последних являются разными.
6. Однофазная электрическая цепь переменного тока с активным сопротивлением R. Кривые напряжения тока и мгновенной мощности. Векторная диаграмма U и I.
|
|
Участок цепи, содержащий активное сопротивление (рис. 2.6).

Рис. 2.6
Зададимся изменением тока в резисторе по синусоидальному закону
i(t) = ImR sin(ωt + ψi).
Воспользуемся законом Ома для мгновенных значений тока и напряжения
u(t) = R i(t)
и получим
(2.13)
u(t) = R ImR sin(ωt + ψi).
Формальная запись синусоидального напряжения имеет вид
(2.14)
u(t) = UmR sin(ωt + ψu)
Соотношения (2.13) и (2.14) будут равны если будут выполнены условия равенства амплитуд и фаз
(2.15)
UmR = R ImR,
(2.16)
ψu = ψi.
Соотношение (2.15) может быть записано для действующих значений
(2.17)
UR = R IR.
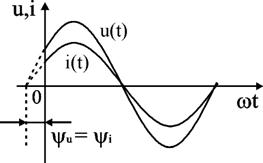
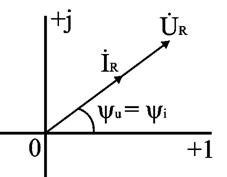
Соотношение (2.16) показывает, что фазы напряжения и тока в резисторе совпадают. Графически это представлено на временной диаграмме (рис. 2.7) и на комплексной плоскости (рис. 2.8).
Мгновенное значение мощности. В цепи, содержащей активное, индуктивное и емкостное сопротивления, в которой ток I и напряжение u в общем случае сдвинуты по фазе на некоторый угол?, мгновенное значение мощности р равно произведению мгновенных значений силы тока i и напряжения u. Кривую мгновенной мощности р можно получить перемножением мгновенных значений тока i и напряжения u при различных углах?t (рис. 199, а. Из этого рисунка видно, что в некоторые моменты времени, когда ток и напряжение направлены навстречу друг другу, мощность имеет отрицательное значение. Возникновение в электрической цепи отрицательных значений мощности является вредным. Это означает, что в такие периоды времени приемник возвращает часть полученной электроэнергии обратно источнику; в результате уменьшается мощность, передаваемая от источника к приемнику. Очевидно, что чем больше угол сдвига фаз?, тем больше время, в течение которого часть электроэнергии возвращается обратно к источнику, и тем больше возвращаемая обратно энергия и мощность.
|
|
Кривые. Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь?
При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.
Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения. В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления.
Действующее значение переменного тока - это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе.
Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.
Мощность Р постоянного тока I, проходящего через сопротивление r, будет Р = Р2r.
Мощность переменного тока выразится как средний эффект мгновенной мощности I2r за целый период или среднее значение от (Im х sinωt)2 х r за то же время.
Пусть среднее значение t2 за период будет М. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I2r = Mr, откуда I = √M,
Величина I называется действующим значением переменного тока.
Среднее значение i2 при переменном токе определим следующим образом.
Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени.
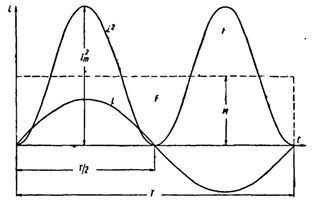
Действующее значение переменного тока
Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i) во второй половине периода, будучи возведены в квадрат, дают положительные величины.
Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно 1/2I2m. Следовательно, М = 1/2I2m
Так как действующее значение I переменного тока равно I = √M, то окончательно I = Im / √2
Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид:
U = Um / √2,E= Em / √2
Действующие значения переменных величин обозначаются прописными буквами без индексов (I, U, Е).
На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.
ВЕКТОРНАЯ ДИАГРАММА
графич. изображение значений физ. величин, изменяющихся по гармони ч. закону, и соотношений между ними при помощи векторов. В. д. широко применяют в электротехнике, акустике, оптике и т. д. В. д. в электротехнике - графич. изображение в виде векторов синусоидально изменяющихся электрич. величин. На рис. дана В. д. силы тока i = Im sin(2ПИft- 30°) и электрич. напряжения и = Um sin2GBft (i,u - мгновенные значения величин, Im, Um - их амплитуды, f - частота, t - время, 30 - нач. фаза тока при t = 0).
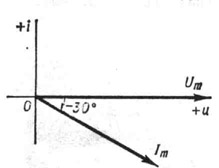
Векторная диаграмма
7. Определение средней мощности для активной нагрузки.
Мощность переменного тока есть произведением напряжения на ток. Для переменного тока, величина которого изменяется со временем произведение мгновенных значений в данный момент времени тока и напряжения даст мгновенную мощность. Она будет равна нулю в те моменты, когда ток проходит через нуль и максимальна при амплитудных значениях. Эту мощность достаточно сложно измерить, да и необходимости в этом особой нет. Так как она не показательна. На практике используют среднее значение мгновенной мощности за период. И называется она активной.
Если цепь переменного тока состоит только из активного сопротивления, то средняя мощность в ней будет равна произведению среднего тока на среднее напряжение. При этом от источника тока энергия передается потребителю, где преобразуется в другие виды энергии.