Определение. Множество точек 
пространства, координаты которых в некоторой прямоугольной декартовой системе координат удовлетворяют уравнению
, 
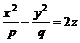(8.1)
называют гиперболическим параболоидом.
Нетрудно показать, что ось 
является осью симметрии поверхности (8.1) (ее называют осью параболоида), а координатные плоскости 
и 
являются плоскостями симметрии (их называют главными плоскостями этой поверхности). Начало координат для гиперболического параболоида является точкой пересечения этой поверхности с ее осью и называется вершиной.
1) Сечения поверхности (8.1) плоскостями 
определяются уравнениями
(8.2)
а) Если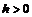 
, то соотношения (8.2) равносильны системе
(8.3)
Уравнения (8.3) определяют гиперболу, расположенную в плоскости 
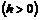. Ее центр находится в точке 
, действительная ось параллельна оси 
, мнимая – оси 
. Длины полуосей
и 
изменяются от 
до 
при изменении 
от до соответственно.
б) Если 
, то соотношения (8.2) равносильны системе
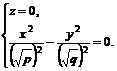(8.4)
Уравнения (8.4) определяют пару пересекающихся прямых
и 
,
расположенных в плоскости и целиком лежащих на поверхности (8.1).
в) Если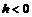 
, то соотношения (8.2) равносильны системе
(8.5)
Уравнения (8.5) определяют гиперболу, расположенную в плоскости 
. Ее центр находится в точке , действительная ось параллельна оси , мнимая – оси . Длины полуосей
и 
изменяются от до при изменении от до 
соответственно.
2) Сечения гиперболического параболоида плоскостями 
определяются уравнениями
или 
(8.6)
Уравнения (8.6) определяют параболу, расположенную в плоскости . Ее вершина находится в точке 
, ось параллельна оси , ветви направлены «вверх». При эта парабола расположена в плоскости , и ее уравнения имеют вид
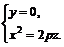(8.7)
3) Сечения гиперболического параболоида плоскостями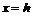 
определяются уравнениями
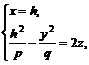или 
(8.8)
Уравнения (8.6) определяют параболу, расположенную в плоскости 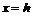. Ее вершина находится в точке 
, ось параллельна оси , ветви направлены «вниз». При эта парабола расположена в плоскости 
, и ее уравнения имеют вид
(8.9)
Приведенные рассуждения показывают, что гиперболический параболоид может быть получен движением параболы (8.7) по параболе (8.9) (при движении параболы (8.7) ее вершина перемещается по параболе (8.9)) или наоборот.
Приведенные рассуждения и сделанные при этом выводы позволяют получить представление о форме рассматриваемой поверхности.
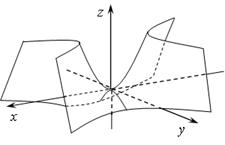
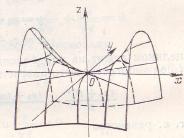
а) б)
в) г)
Рис. 16. Гиперболический параболоид и его сечения.
Поверхности вращения
Пусть 
– плоская линия и 
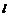– прямая, принадлежащая плоскости плоской линии.
Определение. Поверхность, получающуюся вращением плоской линии вокруг прямой, лежащей в плоскости плоской линии, называют поверхностью вращения.
Прямая, вокруг которой вращается плоская линия , называется осью вращения, а вращающаяся линия – первоначальным меридианом.
Пусть 
– секущая плоскость.
1) Если 
, то сечением служит окружность, проходящая через точку 
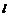с центром на оси . Такие окружности называют параллелями.
2) Если : 
, то сечение – линия 
– меридиан. Любой меридиан поверхности вращения и первоначальный меридиан – равные линии.
Введем в рассмотрение прямоугольную декартову систему координат 
так, чтобы ось вращения 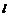совпала с осью .
Теорема 9.1. Пусть относительно прямоугольной декартовой системы координат на плоскости задан первоначальный меридиан поверхности вращения 
уравнениями
. (9.1)
Тогда уравнение поверхности , образованной вращением линии вокруг оси будет иметь вид
. (9.2)
► Пусть – первоначальный меридиан поверхности вращения ,
заданный уравнениями , т.е. 
. И пусть 
– меридиан и 
– параллель: 
. Тогда 
. Так как 
, то 
. Точка 
– центр окружности-параллели 
. Так как точки 
и 
принадлежат одной и той же параллели , то 
, где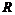 
– радиус окружности-параллели. Но 
.
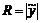Следовательно
Рис. 15. Поверхность вращения.
,
.
Тогда 
, и уравнение поверхности вращения имеет вид
. ◄
Рассмотрим некоторые примеры поверхностей вращения.
1) Пусть : 
– эллипс в плоскости 
.
Так как показано, что 
и , то уравнение поверхности вращения имеет вид
или 
. (9.3)
Рис. 16. Эллипсоид вращения. (9.3) – эллипсоид вращения (Рис. 16).
В частности, если – окружность: 
, то, учитывая, что и , получаем уравнение поверхности вращения
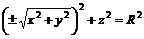или 
(9.4)
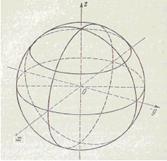
(9.4) – сфера с центром в начале координат радиуса 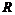(Рис. 17).
Рис. 17. Сфера.
2) Если : 
– гипербола в плоскости , то, учитывая, что и , уравнение поверхности вращения имеет вид
или
(9.5)
Рис. 18. Однополостный (9.5) – однополостный гиперболоид вращения.
гиперболоид вращения
3) Если : 
– гипербола в плоскости , то с учетом соотношений и , уравнение поверхности вращения имеет вид
или 
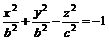(9.6)
(9.6) – двуполостный гиперболоид вращения (Рис. 19).
Рис. 19. Двуполостный Рис. 20. Прямой круговой конус
гиперболоид вращения.
4) Если : 
– прямая в плоскости . Тогда при и получаем уравнение поверхности вращения:
или 
(9.7)
(9.7) – прямой круговой конус (Рис. 20).
5) : 
– парабола в плоскости . Уравнение поверхности вращения имеет вид:
или 
(9.8)
(9.8) – параболоид вращения (Рис. 21).
6) : 
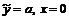– прямая, параллельная оси 
. Учитывая, что и , получаем уравнение поверхности вращения:
или 
(9.9)
(9.9) – прямой круговой цилиндр (Рис.22).
Рис.21. Параболоид вращения. Рис.22. Прямой круговой цилиндр
7) : 
– окружность в плоскости , не пересекающая ось . Тогда при и имеем:
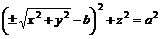
(9.10)
(9.10) – тор (Рис. 23).
Рис. 23. Тор.