Упрощение выражений, содержащих радикалы
Домашнее задание №36.7-№36.12(в,г)
Повторение теоретических фактов
Повторим некоторые теоретические положения.
Определение:
Корнем n-й степени из неотрицательного числа а называется такое неотрицательное число b, которое при возведении в степень n дает число а.
Приведем математическую запись определения:
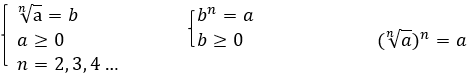
Например: 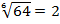 , т. к.
, т. к. 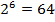 ;
; 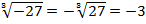 , т. к.
, т. к. 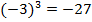 ,
,
Напомним, что арифметическим корнем называется неотрицательный корень. В нашем случае 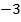 – отрицательное число, но
– отрицательное число, но 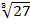 – положительное, таким образом,
– положительное, таким образом, 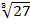 – это арифметический корень.
– это арифметический корень.
Вспомним основные свойства арифметических корней:
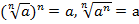 при
при 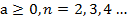
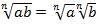 , при
, при 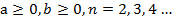 (теорема 1);
(теорема 1);
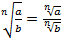 , при
, при 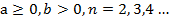 (теорема 2);
(теорема 2);
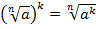 , при
, при 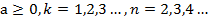 (теорема 3);
(теорема 3);
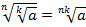 , при
, при 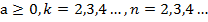 (теорема 4);
(теорема 4);
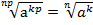 при
при 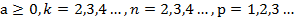 (теорема 5);
(теорема 5);
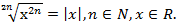
Упрощение выражений, примеры
При решении задач мы пользуемся определением и свойствами корня n-й степени.
Пример 1 – упростить и выполнить действия:
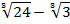
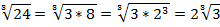
В результате преобразования получили выражение:
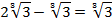
Мы видим основной принцип решения подобных задач: если под корнем стоит составное число, нужно разложить его на простые множители, и тогда, возможно, будет легко заметить решение задачи.
Пример 2:
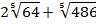
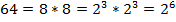
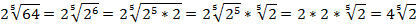
Разложим составное число 486 на простые множители:
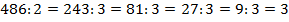
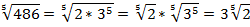
В результате преобразований получаем:
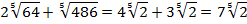
Пример 3 – выполнить умножение:
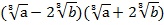
Очевидно, что для решения данного задания необходимо применить формулу сокращенного умножения, а именно: 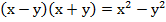 – формула разности квадратов.
– формула разности квадратов.
В нашем случае 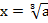 ,
, 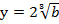 , получаем:
, получаем:
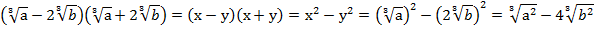
Пример 4 – выполнить умножение:
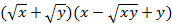
В данном случае нужно заметить другую формулу сокращенного умножения: 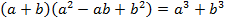 – сумма кубов;
– сумма кубов;
В нашем случае 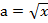 ,
, 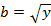 , получаем:
, получаем:
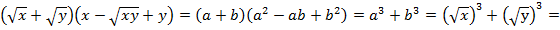
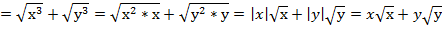
Комментарий: поскольку в заданном примере переменные х и у стояли под квадратным корнем, то они неотрицательны, значит, имеем право снять модуль.
Сокращение дробей, примеры
Одной из типовых задач является задача на сокращение дробей.
Пример 5 – сократить дробь:
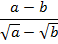
Отметим некоторые ограничения. Для того чтобы существовали заданные корни, необходимо выполнение условий: 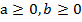 . Для того чтобы существовала дробь:
. Для того чтобы существовала дробь: 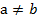 .
.
Преобразуем числитель дроби:
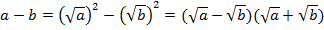
Таким образом, заданную дробь можно записать в следующем виде:
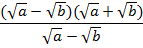
Поскольку мы заранее оговорили, что знаменатель не равен нулю, т. е. 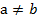 , имеем право сократить дробь:
, имеем право сократить дробь:
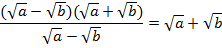
Пример 6:
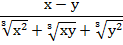
В данном случае также нужно воспользоваться формулой сокращенного умножения.
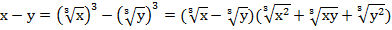
Таким образом, заданную дробь можно записать в следующем виде:
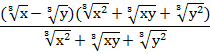
Чтобы иметь право сократить дробь, оговорим, что знаменатель ее не должен быть равен нулю, для этого х и у не должны одновременно быть равны нулю, тогда получаем ответ:
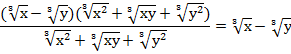
Преобразование сложных корней к простому виду
Пример 7 – преобразовать выражение к виду 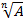 :
:
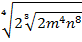
Внесем двойку под кубический корень:
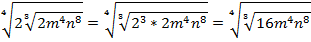
Согласно теореме о взятии корня из корня, перемножим показатели корней:
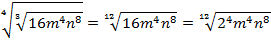
Согласно теореме о корне из произведения, получим:
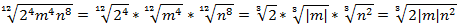
Пример 8:
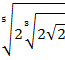
Постепенно вносим множители под знак внутреннего корня и перемножаем показатели корней:
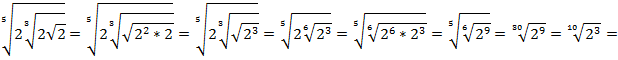
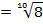
Пример 9 – упростить выражение:
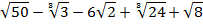
Представим все составные числа в виде простых чисел:
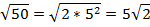
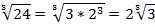
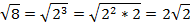
В результате преобразований получили выражение:
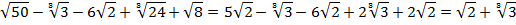
Решение более сложных примеров
Пример 10 – вычислить:
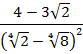
В знаменателе стоит выражение, распишем его по формуле квадрата разности:
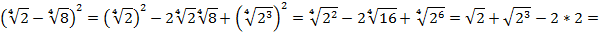
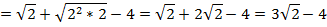
После преобразования получаем дробь:
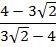
Вынесем в знаменателе минус за знак дроби:
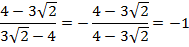
Итак, мы вспомнили основные теоретические факты о корнях n-й степени и научились решать некоторые типовые задачи с радикалами. Мы решили много различных примеров, на следующем уроке мы продолжим изучение данной темы.