Как в электрической цепи сила тока зависит от приложенного напряжения и от сопротивления, оказываемого элементами цепи, так и в магнитной цепи магнитный поток Ф зависит от приложенной магнитодвижущей силы (м.д.с.) численно равной Iw и от сопротивления R магнитному потоку:
(1)
Эта формула выражает закон Ома для магнитной цепи.
Магнитное сопротивление RМ определяют в зависимости от длины силовых линий l (м), площади поперечного сечения силового потока S (м2) и абсолютной магнитной проницаемости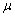 
а (Вб/А 
м):
(2)
Не трудно уловить аналогию формулы №2 формуле: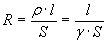 
- для определения сопротивления проводника электрическому току.
Подставим в выражение №1 вместо RМ его значение из формулы №2, получим:
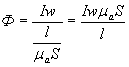(3)
При расчете магнитной цепи задача чаще всего сводится к определению необходимой э.д.с. для того, чтобы получить в магнитопроводе определенный магнитный поток или заданную магнитную индукция, например воздушном зазоре. Ниже излагается путь расчета применительно к магнитопроводу, показанному на рисунке №1.
Магнитный поток замыкается через сердечник и воздушный зазор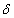 
. Отдельные участки сердечника могут быть выполнены из различных материалов и неодинакового сечения. Через сечение каждого из участков каждого из участков сердечника проходит один и тот же магнитный поток Ф:
и т.д.
По закону Ома для магнитной цепи
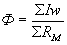(4)
где 
-алгебраическая сумма ампер-витков, численно равная общей м.д.с. обмотки; 
- сумма магнитных сопротивлений участков, на которых индукция В напряженность Н постоянны.
Пользуясь формулой № 2 для магнитной цепи, показанной на рисунке №1, можно найти:
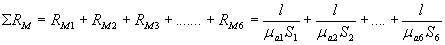(6)
где 
, 
,….., 
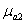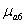- магнитные проницаемости участков магнитной цепи.
После подстановки значения из №6 в №4
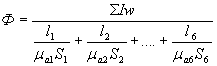
откуда
(7)
Ввиду того что
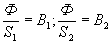
а также что
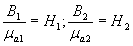и т.д.
равенство №7 принимает следующий вид:
(8)
где произведения Н1 l1 ; H2 l2 являются м.д.с. отдельных участков.
16. Электромагнитная индукция.
Это когда всякое изменение магнитного потока пронизывает поток или контур наводит ЭДС в данном витке. Величина, возникающая ЭДС пропорцианальна числу витков, величине магнитного потока и измениению магнитного потока: e= - dФ/dt.
Перед приизводной стоит знак «-«,который показывает,что ЭДС,проводимое в ветке создает свой магнитный поток, который направлен противоположно внешнему магнитному потоку и если внешний магнитный поток приближается к витку,то внутренний поток старается его ослабить, уменьшить, а если виток удаляется от внешнего поля, то внутреннее поле старается поддержать магнитный поток.
17. Индуктивность
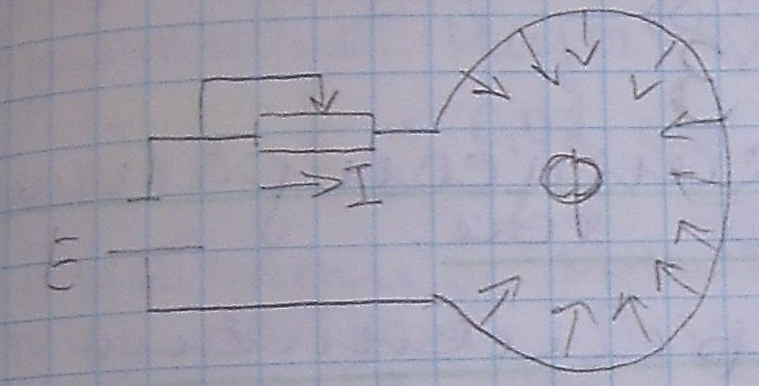
Ф= Iw/Rµ
Rµ-магнитное сопротивление витка
w- число витков.
Если число витков в цепи не меняется,то Ф не изменяется. Если изменять величину R на dr, то ток будет изменяться и будет изменяться величина магнитного потока Ф на dФ.
dr→ dI →dФ = wdI/ Rµ
По закону электромагнитной индукции при применении магнитного потока,создавать витком в контуре возникает ЭДС:
e=- wdФ/dt= - 
dI/ Rµ dt= - L dI/dt
L dI/dt –коффициент индуктивности
Индуктивность – международ. Ед-ца [L]=Гн (Генри)
Индуктивность –коэффициент пропорциональности между ЭДС и скоростью изменения тока в цепи dI/dt
Если ток не изменяется dI=0, L =0.
Индуктивность зависит от числа витков в квадрате и обратно пропорционально магнитному сопротивлению среды.
18. Понятие о переменном синусоидальном токе
На постоянном токе ЭДС всегда постоянно, ток течет от + к – всегда и может изменяться при изменении сопротивления по величине, т.е. постоянным во времени. Переменный ток изменяется по величине и по направлению
i-мгновенное значение тока.
В странах СНГ переменный ток f=50 ГЦ
Интервал через, который переменный ток периодически повторяет свои значения называется периодом(Т):
Т=1/f= 0,02сек→360®
Наибольшее мгновенное значение тока, называется амплитудой и обознач. 
: I = sin wt, по этому этот ток называется СИНУСОИДАЛЬНЫМ
19. Получение синусоидального переменного тока.
В однородном магнитном поле с индукцией В, между полюсами постоянного магнита расположена катушка их w витков. Катушка приводится во вращательное движение вокруг оси О внешней силой.
На рисунке показано 3 положения катушки при повороте на ¼ окружности. Площадь поперечного сечения витки обозначены S. При 1 положении виток будет пронизывать магнитный поток 1: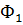 
=B S cos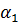 
При втором положении: 
=B S cos 
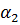, 3: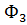 
=B S cos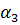 
- угол между плоскостью катушки и магнитным потоком: = wt
w- частота вращения катушки: w=2πf
тогда: 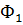=B S cos 
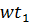, =B S cos 
, 
=B S cos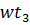 
= w 
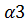, = w 
, 
= w 
В любой момент времени: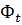 
=B S cos 
t- мгновенный момент времени.
Если обозначим BS= 
, -мах(амплитудное) значение магнитного потока 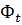= cos wt
Витки будет пронизывать магнитный поток,изменяющийся по закону косинуса, т.е. виток все время будет пронизывать изменяющий магнитный поток, значит в витке будет образовываться по з-ну электромагнитной индукции ЭДС: e=-W dФ/dt
Как видно из рис магнитный поток по направлению не изменяется,но поскольку меняется угол витка, то в ней каждая ¼ окружности будет изменятся и величина направл. Тока и ЭДС
Периодич выражение ЭДС: e = W w sin wt
отсюда видно,что ЭДС будет изменятся по синусоидальному закону.
=W w , е = sin wt
Магнитный поток изменяется по з-ну косинуса, а ЭДС по з-ну синуса, то они сдвинуты на 90® между собой или находятся в противофазе.
20. Действующее значение переменного тока
r1=r2=r
i = sin wt
Определение количества тепла Q, которое выдел в сопротивлении за одинаковое время одного периода T=0.02с
Q= r1 
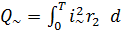=T
t
Приравниваем эти уравнения между собой:
=I= 
В действит значениях проградуированы все приборы раб на переменном токе. Действит значение переменного тока = такой величине постоянного тока, которое производит одинаковый тепловой эффект при одних и тех же условиях за одно и тоже время.
Фазовый сдвиг
1. Цепь с резистивным элементом.Сдвиг по фазе между напряжением и током цепи:
| +J |
| U R |
| İR |
| +1 |
2. Цепь с емкостным элементом.Сдвиг по фазе между напряжением и током цепи:
φ = ψ u - ψ i = 0º - 90º = - 90º. (ток опережает по фазе напряжение на 90)
3. Цепь с индуктивным элементом. Сдвиг по фазе между напряжением и током цепи
φ = 0° – (-90°) = +90
Таким образом, синусоида тока в цепи с идеальной индуктивной катушкой отстает от синусоиды напряжения на угол 90º.