Расчет теоретической части

Аппаратная и программная реализация СЛУ

При аппаратной реализации необходимо синтезировать схему логического управления для объекта, представляющего собой резервуар – смеситель, в котором при смешивании двух исходных материалов производится готовый продукт (рис.1). Контролируемыми параметрами являются: Q ₁ = Х₁ – концентрация 1-го компонента в готовом продукте, Q ₂ = Х₂ – концентрация 2-го компонента, L= Х₃ – уровень готового продукта в резервуаре.

Задача системы управления состоит в поддержании определенного соотношения компонентов в продукте и запаса готового продукта, т.е. его уровня в резервуаре.

Для управления могут использоваться клапаны 1, 2 на трубопроводах подачи исходных материалов и 3 – на трубопроводе слива готового продукта.

Входные параметры X_1, X_2, X₃ системы управления рассматриваются как дискретные, принимающие значение “0” при нормальной величине соответствующего технологического параметра или “1” – при отклонениях от нормы.

О

Рис. 1.Резервуар-смеситель

В зависимости от постановки задачи управления за единичное значение входной переменной может приниматься ее величина ниже нормы или выше нормы. Очевидно, что если одновременно Х₁ = 1 и Х₂ = 1, то это означает неисправность одного из концентратомеров.

Управляющие переменные также является дискретными, им соответствуют сигналы прикрытия U₁, U₃, U₅ или приоткрытия U₂, U₄, U₆ клапанов. В такой системе возможно несколько вариантов реализации системы управления.

Рассматривая последовательно все возможные состояния системы, составляем таблицу истинности. Далее на основании таблицы истинности записываются логические выражения для управляющих воздействий в совершенной дизъюнктивной нормальной форме (СДНФ) или совершенной конъюнктивной нормальной форме (СКНФ). Представление зависимостей выходных переменных от входных в этих формах не является оптимальным, поэтому следующий этап – минимизация логических функций (получение МДНФ). Далее при аппаратной реализации системы логического управления составляется структурная схема устройства, ориентированная на использование выбранного базиса логических элементов.

Следующий этап – проверка работоспособности разработанной принципиальной схемы СЛУ.

 

Задание

С целью упрощения построения таблицы истинности разрабатываемой СЛУ выдача задания формализована, причем полученная таблица истинности не соответствует объекту управления.

Для нечетных номеров схема синтезируется на ЛЭ 2И-НЕ.

Теоретическая часть задания включает в себя следующие операции:

1. Минимизацию логических выражений для управляющих переменных:

· табличным способом для первой переменной;

· алгебраическим способом для второй переменной;

· с помощью карт Карно для третьей переменной;

· любым из известных способов для 4-ой.

2. Синтез схемы управления в булевском базисе;

3. Синтез схемы управления в заданном базисе.

Практическая часть задания заключается в монтаже разработанных схем на стенде в лаборатории и проверке их функционирования по таблице истинности.

Исходные данные

Таблица 1. Исходные данные.

 

№ п.п	№ управляющего воздействия	U4	U5	U6	U7
	4, 5, 6, 7				F2

 

 

Расчет теоретической части

По приведённому выше заданию получим двоичную форму чисел U2, U4, U6, U7:

 

U4(16)= 47 U4(2)=01000111

U5(16)= 06 U5(2)=00000110

U6(16)= 04 U6(2)=00000100

U7(16)= F2 U7(2)=11110010

 

Сведем полученные данные в таблицу 2:

 

Таблица 2. Таблица истинности

 

X3	X2	X1	U4	U5	U6	U7

1. Минимизация управляющих переменных U4, U5, U6, U7.

 

1) Используем табличный метод для получения логической функции U4 и ее минимизации:

 

X3	X2	X1	U2

 

 

Запишем таблицу следующего вида:

 

Таблица 3. Табличный метод минимизации

 

 

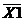
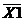
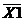
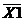
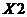
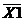
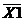
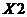
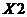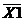
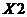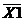
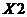
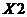
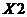
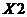
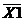
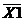
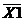
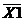
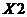
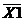
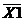
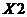
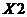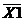
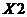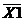
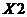
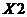
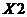
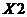
Используя метод, получим:

 

U4 = =

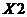
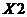
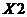
Схема, построенная на элементах 2ИЛИ-НЕ, реализующая логическую функцию U4, изображена на рисунке 2.

Запищем функцию, используя законы Де Моргана:

U4 =

 

 

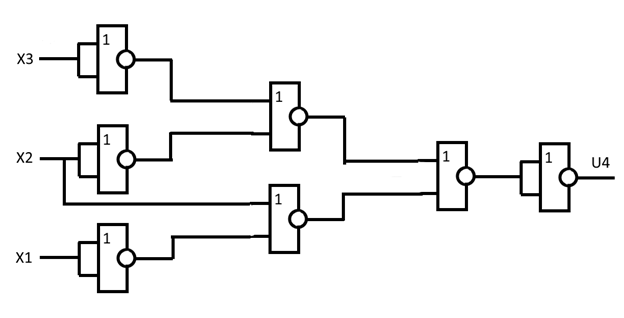
Рис. 2. Логическая схема, реализующая функцию U4.

 

 

2) Используем алгебраический метод для получения логической функции U5 и её минимизации:

X3	X2	X1	U5

 

 

Используя алгебраический метод, получим:

 

U5 =

 

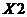
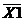
Запищем функцию, используя законы Де Моргана:

U5=

Схема, построенная на элементах 2ИЛИ-НЕ, реализующая логическую функцию U5 изображена на рисунке 3.

Рис. 3. Логическая схема, реализующая функцию U5.

 

3) Получим и минимизируем U6 с помощью карт Карно:

U6 =

 

X3	X2	X1	U6

 

 

Построим карту Карно:

Таблица 4. Карта Карно

 

	Х3Х2	Х3		Х2

 

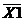
Используя построенную таблицу и метод, получим:

U6 =

Запищем функцию, используя законы Де Моргана:

U6 =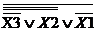

 

Схема, построенная на элементах 2ИЛИ-НЕ, реализующая логическую функцию U6 изображена на рисунке 4.

 

 

 

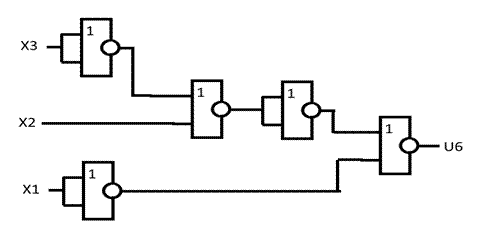
Рис. 4. Логическая схема, реализующая функцию U6.

4) Получим и минимизируем U7 с помощью карт Карно:

 

X3	X2	X1	U7

 

Таблица 5. Карта Карно

 

	Х3Х2	Х3		Х2

 

Используя построенную таблицу и метод, получим:

 

U7 = X2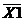

Запищем функцию, используя законы Де Моргана:

 

U7 =

 

 

Схема, реализующая логическую функцию U7, изображена на рисунке 5.

 

 

Рис. 5. Логическая схема, реализующая функцию U7