Методы оптимизации. Теория игр и исследование операций

46. В распоряжении комплекса ПВО имеется четыре разработанных образца зенитных управляемых ракет: А₁, А₂, А₃, А₄, предназначенных для стрельбы по самолетам. Известны типы самолетов противника B₁, B₂, B₃, B₄, B₅, которые он может применять, однако известно заранее - в какой пропорции. Вероятности поражения самолета противника при применении каждого типа вооружения заданы матрицей

Требуется, исходя из принципов теории игр, обосновать пропорции, в которых надо заказывать вооружение различных типов.

Критерий максимакса.
Критерий максимакса ориентирует статистику на самые благоприятные состояния природы, т.е. этот критерий выражает оптимистическую оценку ситуации.

A_i	П₁	П₂	П₃	П₄	П₅	max(a_ij)
A₁	0.2	0.4	0.6	0.4	0.7	0.7
A₂	0.3	0.4	0.6	0.5	0.8	0.8
A₃	0.4	0.5	0.6	0.5	0.8	0.8
A₄	0.7	0.3	0.5	0.2	0.1	0.7

Выбираем из (0.7; 0.8; 0.8; 0.7) максимальный элемент max=0.8
Вывод: выбираем стратегию N=2.
Критерий Байеса.
По критерию Байеса за оптимальные принимается та стратегия (чистая) A_i, при которой максимизируется средний выигрыш a или минимизируется средний риск r.
Считаем значения ∑(a_ijp_j)
∑(a_1,jp_j) = 0.2*0.2 + 0.4*0.2 + 0.6*0.2 + 0.4*0.2 + 0.7*0.2 = 0.46
∑(a_2,jp_j) = 0.3*0.2 + 0.4*0.2 + 0.6*0.2 + 0.5*0.2 + 0.8*0.2 = 0.52
∑(a_3,jp_j) = 0.4*0.2 + 0.5*0.2 + 0.6*0.2 + 0.5*0.2 + 0.8*0.2 = 0.56
∑(a_4,jp_j) = 0.7*0.2 + 0.3*0.2 + 0.5*0.2 + 0.2*0.2 + 0.1*0.2 = 0.36

A_i	П₁	П₂	П₃	П₄	П₅	∑(a_ijp_j)
A₁	0.04	0.08	0.12	0.08	0.14	0.46
A₂	0.06	0.08	0.12	0.1	0.16	0.52
A₃	0.08	0.1	0.12	0.1	0.16	0.56
A₄	0.14	0.06	0.1	0.04	0.02	0.36
p_j	0.2	0.2	0.2	0.2	0.2

Выбираем из (0.46; 0.52; 0.56; 0.36) максимальный элемент max=0.56
Вывод: выбираем стратегию N=3.
Критерий Лапласа.
Если вероятности состояний природы правдоподобны, для их оценки используют принцип недостаточного основания Лапласа, согласно которого все состояния природы полагаются равновероятными, т.е.:
q₁ = q₂ =... = q_n = 1/n.
q_i = 1/5

A_i	П₁	П₂	П₃	П₄	П₅	∑(a_ij)
A₁	0.04	0.08	0.12	0.08	0.14	0.46
A₂	0.06	0.08	0.12	0.1	0.16	0.52
A₃	0.08	0.1	0.12	0.1	0.16	0.56
A₄	0.14	0.06	0.1	0.04	0.02	0.36
p_j	0.2	0.2	0.2	0.2	0.2

Выбираем из (0.46; 0.52; 0.56; 0.36) максимальный элемент max=0.56
Вывод: выбираем стратегию N=3.
Критерий Вальда.
По критерию Вальда за оптимальную принимается чистая стратегия, которая в наихудших условиях гарантирует максимальный выигрыш, т.е.
a = max(min a_ij)
Критерий Вальда ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.

A_i	П₁	П₂	П₃	П₄	П₅	min(a_ij)
A₁	0.2	0.4	0.6	0.4	0.7	0.2
A₂	0.3	0.4	0.6	0.5	0.8	0.3
A₃	0.4	0.5	0.6	0.5	0.8	0.4
A₄	0.7	0.3	0.5	0.2	0.1	0.1

Выбираем из (0.2; 0.3; 0.4; 0.1) максимальный элемент max=0.4
Вывод: выбираем стратегию N=3.
Критерий Севиджа.
Критерий минимального риска Севиджа рекомендует выбирать в качестве оптимальной стратегии ту, при которой величина максимального риска минимизируется в наихудших условиях, т.е. обеспечивается:
a = min(max r_ij)
Критерий Сэвиджа ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.
Находим матрицу рисков.
Риск – мера несоответствия между разными возможными результатами принятия определенных стратегий. Максимальный выигрыш в j-м столбце b_j = max(a_ij) характеризует благоприятность состояния природы.
1. Рассчитываем 1-й столбец матрицы рисков.
r₁₁ = 0.7 - 0.2 = 0.5; r₂₁ = 0.7 - 0.3 = 0.4; r₃₁ = 0.7 - 0.4 = 0.3; r₄₁ = 0.7 - 0.7 = 0;
2. Рассчитываем 2-й столбец матрицы рисков.
r₁₂ = 0.5 - 0.4 = 0.1; r₂₂ = 0.5 - 0.4 = 0.1; r₃₂ = 0.5 - 0.5 = 0; r₄₂ = 0.5 - 0.3 = 0.2;
3. Рассчитываем 3-й столбец матрицы рисков.
r₁₃ = 0.6 - 0.6 = 0; r₂₃ = 0.6 - 0.6 = 0; r₃₃ = 0.6 - 0.6 = 0; r₄₃ = 0.6 - 0.5 = 0.1;
4. Рассчитываем 4-й столбец матрицы рисков.
r₁₄ = 0.5 - 0.4 = 0.1; r₂₄ = 0.5 - 0.5 = 0; r₃₄ = 0.5 - 0.5 = 0; r₄₄ = 0.5 - 0.2 = 0.3;
5. Рассчитываем 5-й столбец матрицы рисков.
r₁₅ = 0.8 - 0.7 = 0.1; r₂₅ = 0.8 - 0.8 = 0; r₃₅ = 0.8 - 0.8 = 0; r₄₅ = 0.8 - 0.1 = 0.7;

A_i	П₁	П₂	П₃	П₄	П₅
A₁	0.5	0.1		0.1	0.1
A₂	0.4	0.1
A₃	0.3
A₄		0.2	0.1	0.3	0.7

Результаты вычислений оформим в виде таблицы.

A_i	П₁	П₂	П₃	П₄	П₅	max(a_ij)
A₁	0.5	0.1		0.1	0.1	0.5
A₂	0.4	0.1				0.4
A₃	0.3					0.3
A₄		0.2	0.1	0.3	0.7	0.7

Выбираем из (0.5; 0.4; 0.3; 0.7) минимальный элемент min=0.3
Вывод: выбираем стратегию N=3.
Критерий Гурвица.
Критерий Гурвица является критерием пессимизма - оптимизма. За оптимальную принимается та стратегия, для которой выполняется соотношение:
max(s_i)
где s_i = y min(a_ij) + (1-y)max(a_ij)
При y = 1 получим критерий Вальде, при y = 0 получим – оптимистический критерий (максимакс).
Критерий Гурвица учитывает возможность как наихудшего, так и наилучшего для человека поведения природы. Как выбирается y? Чем хуже последствия ошибочных решений, тем больше желание застраховаться от ошибок, тем y ближе к 1.
Рассчитываем s_i.
s₁ = 0.5*0.2+(1-0.5)*0.7 = 0.45
s₂ = 0.5*0.3+(1-0.5)*0.8 = 0.55
s₃ = 0.5*0.4+(1-0.5)*0.8 = 0.6
s₄ = 0.5*0.1+(1-0.5)*0.7 = 0.4

A_i	П₁	П₂	П₃	П₄	П₅	min(a_ij)	max(a_ij)	y min(a_ij) + (1-y)max(a_ij)
A₁	0.2	0.4	0.6	0.4	0.7	0.2	0.7	0.45
A₂	0.3	0.4	0.6	0.5	0.8	0.3	0.8	0.55
A₃	0.4	0.5	0.6	0.5	0.8	0.4	0.8	0.6
A₄	0.7	0.3	0.5	0.2	0.1	0.1	0.7	0.4

Выбираем из (0.45; 0.55; 0.6; 0.4) максимальный элемент max=0.6
Вывод: выбираем стратегию N=3.
Таким образом, в результате решения статистической игры по различным критериям чаще других рекомендовалась стратегия A₃.

47. Предприятие изготавливает и продает краску двух видов: для внутренних и внешних работ. Для производства краски используется два исходных ресурса А и В. Расходы ресурсов А и В на 1 тонну соответствующих красок и запасы этих ресурсов на складе приведены в таблице:

Ресурс	Расход ресурсов	Запас ресурса
Краска для внутренних работ	Краска для внешних работ
А
В

Цена за одну тонну краски для внутренних работ составляет 2000 рублей, краска для наружных работ продается по 1000 рублей за одну тонну. Требуется определить, какое количество краски каждого вида следует производить предприятию, чтобы получить максимальный доход. Во сколько следует оценить ресурсы, в случае их продажи.

Построим математическую модель задачи.

Производственному менеджеру компании необходимо спланировать объем производства красок так, чтобы максимизировать доход от их продажи.

Переменными модели являются:

x₁ – суточный объем производства краски для внутренних работ,

x₂ – суточный объем производства краски для наружных работ.

Суммарный суточный доход от реализации произведенной продукции равен:

Целью компании является нахождение среди всех допустимых значений переменных x₁, x₂, таких, которые максимизируют построенную целевую функцию.

Перейдем к ограничениям, которым должны удовлетворять переменные x₁, x₂:

расход исходных ресурсов не должен превышать их запаса, поэтому:

объем производства не может быть отрицательным, поэтому:

Таким образом, математическая модель рассматриваемой задачи примет вид:

Решим ее графически:

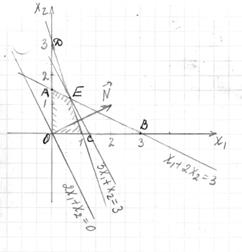OACE – область допустимых решений

Нанесем

Далее будем перемещать целевую функцию вдоль . Целевая функция покидает область допустимых решений в точке Е. Там находится максимум целевой функции. Найдем координаты точки Е: