Потоковые модели распределенных вычислений

 

Потоковые модели и проблема блокировки вычислений. Потоковые модели – мощное и выразительное средство выявления внутреннего параллелизма программ, которое может быть использовано для повышения производительности вычислительных систем. Потоковые вычисления реализуются по мере готовности данных. За последние тридцать лет потоковые принципы обработки как альтернатива концепции Дж. фон Неймана оказали большое влияние на исследования языков программирования, параллельной компиляции, распределенных вычислений, обработки сигналов, реконфигурируемых архитектур и суперкомпьютеров с массовым параллелизмом.

Часто потоковая обработка непосредственно ассоциируется с машинами, управляемыми потоками данных. Распространенной формой представления программы для них является граф потоков данных, существенное свойство которого заключается в однократном присваивании, или отсутствии повторной входимости. Известны языки для программирования машин потоков данных, например, язык однократного присваивания Sisal. Сразу же подчеркнем, что понятие "потоковая модель" в данном курсе используется в ином контексте, без привязки к архитектуре, управляемой потоками данных. Потоковая организация обработки понимается как использование информационных связей между частично упорядоченными действиями программы для реализации заложенного в ней параллелизма.

Потоковая модель распределенной программы рассматривается как множество процессов, взаимодействующих посредством асинхронной посылки сообщений через входные, а иногда и выходные, буферы и инициируемых готовностью входных сообщений.

Обогащение потоковых моделей такими свойствами, как недетерминизм и распределенность процессов программы в вычислительной среде, а также обмен разнородными сообщениями, ставит ряд серьезных проблем, связанных с исследованием разрешимости как самих моделей, так и задач их анализа. "Зависания" программ могут возникнуть, когда процессы взаимно блокируют друг друга из-за отсутствия сообщений во входных буферах либо переполнения выходных буферов. Частными случаями блокировки вычислений являются ситуации тупика (дедлока) и голодания процессов (ливлока). О тупиках речь уже шла в п. 1.2 раздела 1. Тупик, или ситуация бесконечного ожидания, возникает тогда, когда совместно протекающие процессы разделяют ресурсы, но ни одному процессу их не хватает для завершения вычислений, после чего соответствующая часть ресурсов должна быть освобождена. Опасность возникновения дедлоков важно учитывать при использовании систем синхронизации и организации среды взаимодействия процессов. В частности, как уже говорилось в п. 1.2 раздела 1, тупики могут возникать при использовании блокирующего обмена сообщениями, реализуемого в MPI с помощью функций MPI_Send, MPI_Recv. Чтобы избежать тупиков, можно использовать функции неблокирующего обмена MPI_Isend, MPI_Irecv или совмещенных посылки/приема сообщений MPI_Sendrecv. Для обнаружения возможности дедлока, как правило, используются различные графовые модели. Это может быть ориентированный граф, каждая вершина которого соответствует некоторому ресурсному семафору S[i], а дуга (S[i], S[j]) с меткой Pk – возможности последовательного выполнения P-операции процессом Pk над семафорами S[i] и S[j] (это будет рассмотрено в п. 3.1. раздела 3). Наличие в таком графе контура свидетельствует о тупиковой ситуации. Ливлок может возникнуть, если процессам назначаются некоторые приоритеты при доступе к разделяемым ресурсам. Известной интерпретацией ситуаций тупика и голодания является задача о пяти обедающих философах. Тупик возникает всякий раз, когда все пять философов одновременно рассаживаются вокруг круглого стола, в центре которого располагается блюдо со спагетти, и каждый из философов берет по одной вилке, располагающейся слева от него. Вилок всего пять, а для поедания спагетти нужны две вилки, лежащие слева и справа от философа. Предотвратить подобную ситуацию можно, ограничивая число одновременно обедающих философов. Однако при этом не исключено голодание одного из них, если его соседи договорились между собой таким образом, что каждый раз, поочередно сменяя друг друга, опережают этого философа и соответственно забирают вилки то слева, то справа от него.

В параллельных системах дедлоки могут быть обусловлены неудачным выбором алгоритма маршрутизации коммуникационной сети при передаче данных. Известно, что две основные стратегии передачи сообщений – это коммутация каналов и коммутация пакетов. Первая стратегия характеризуется тем, что коммуникационные ресурсы (порты и буферы коммутаторов) резервируются заранее, до посылки сообщения (пакетов данных). Недостаток стратегии передачи сообщений с коммутацией каналов состоит в том, что ресурсы сети могут использоваться неэффективно: пока не завершится передача пакетов, для которых зарезервирован канал, другие пакеты находятся в состоянии ожидания. Этот недостаток преодолевает другая стратегия – коммутация пакетов. Ее суть состоит в том, что сообщения разбиваются на части (пакеты), для передачи которых коммуникационные ресурсы заранее не резервируются. Однако при этом необходимы предварительное разбиение сообщения в пункте отправления и последующая сборка пакетов в пункте назначения. Тупики могут быть обусловлены конкуренцией за право обладания портами и буферами коммуникационной сети. Впрочем, тупик может возникать и в сети с коммутацией каналов. На рис. 2.4 приведен пример такой ситуации. Пары процессов 1, 4 и 2, 3 пытаются обменяться пакетами. Положим, для этого им удается зарезервировать по два входных порта и одному выходному порту каждого из четырех коммутаторов так, как это показано на рис. 2.4. При одновременной посылке сообщений неизбежно возникает тупик: все четыре процесса ждут, когда освободятся выходные порты коммутаторов.

 

 

Рис. 2.4. Тупик в сети с коммутацией каналов

 

Представленный на рис. 2.4 случай соответствует статической маршрутизации. Маршрутизация может быть реализована адаптивно, когда общий буферный пул динамически распределяется между входными и выходными портами. При этом коммутаторы сети учитывают текущий трафик обмена данными. Во избежание тупиковых ситуаций необходимо специальным образом структурировать буферный пул.

Случаи блокировки вычислений не исчерпываются лишь дедлоками и ливлоками. Чтобы это проиллюстрировать, прибегнем к модели, которая уже частично рассматривалась в п. 1.2 раздела 1. Это – SDF-графы. На рис. 2.5, а приведены примеры SDF-графов, вершины которых, напомним, обозначают акторы, а маркировка дуг – число производимых и потребляемых ими токенов. Случай, представленный на рис. 2.5, а, соответствует последовательности гнезд циклов.

Для однократного срабатывания актора 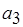необходимо соответственно 10 и 100 срабатываний акторов 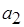и 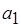. Граф на рис. 2.5, б иллюстрирует случай тупика: акторы 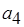, 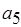взаимно блокируют друг друга. Пример на рис. 2.5, в представляет так называемый несогласованный SDF-граф: актор 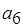при каждом срабатывании производит два токена, передаваемых по дуге 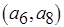, в то время как по дуге 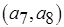передается один. Нетривиального решения уравнения баланса, дающего целое число срабатываний актора 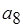, не существует. Ситуацию с актором 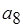можно, с одной стороны, интерпретировать как ливлок по входящей дуге (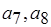). С другой стороны, имеет место "переизбыток" данных, передаваемых по входу ().

 

 

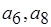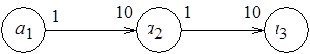
а)

 

 

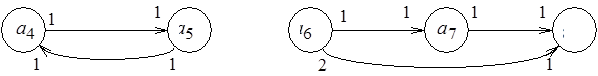
б) в)

Рис. 2.5. Примеры SDF-графов

 

Какие выводы можно сделать из этого примера? Во-первых, для обнаружения возможности блокировок вычислений необходимо учитывать детальную структуру данных, которыми обмениваются процессы. Заметим, в стандарте MPI предусмотрены механизмы, поддерживающие обмен сообщениями из разнотипных данных, или производных типов данных. Однако требовать от стандарта гарантий согласованности данных, поступающих от разных процессов, конечно же, нельзя. Это – забота программиста, которому нужны адекватные модели, поддерживающие информационные зависимости между процессами и соответствующую структуру данных. Во-вторых, SDF-графы не содержат условных ветвлений и альтернативных выборов (слияний) потоков данных. SDF-модели становятся алгоритмически неразрешимыми при введении в них таких конструкций. Это означает, что при этом невозможно дать ответ на вопрос, существует ли нетривиальное, отличное от нуля решение уравнения баланса. В случае, когда оно существует, можно заключить, что в модели SDF отсутствуют тупики и возможно составление беступикового циклического расписания срабатывания акторов при ограниченной памяти данных (токенов). Разумеется, такой "игрушечный" класс моделей вряд ли может быть полезен для исследования поведения сложных программ с циклами, условными операторами и т.д. Необходимы модели, поддерживающие недетерминизм процессов вычислений с произвольно структурированными данными, а в "арсенале" таких моделей должны быть средства предотвращения блокировки вычислений при наличии в программах циклов и альтернативных операторов.

Маркированные потоковые графы. Итак, проблема реализуемости потоковых моделей заключается в согласовании параметров очередей сообщений (входных и выходных буферов) таким образом, чтобы учесть все допустимые истории процессов программы, когда ни один из них не блокируется по рассмотренным выше причинам. Для решения этой проблемы нам понадобятся графы специального вида.

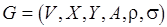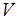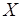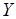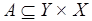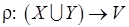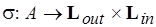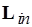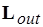Маркированным потоковым графом будем называть шестерку , где – множество вершин (операторов программы); и – множества входных и выходных позиций вершин; – множество информационных дуг; – функция распределения позиций по вершинам; – функция маркировки позиций. Здесь и – множества меток соответственно входных и выходных позиций вершин, в том числе и фиктивных, инцидентных входам и выходам графа. При этом множество включает подмножество ординарных позиций, каждой из которых инцидентна одна дуга, и подмножество позиций для альтернативного выбора входящих потоков данных (select, или slt). В множество 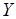включаются подмножество ординарных выходных позиций, а также подмножество позиций, соответствующих альтернативным переключениям (switch, или swh) и ветвлениям (fork, или frk) исходящих потоков данных. В общем случае входная позиция любой вершины 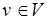может быть ординарной или slt-позицией. Выходная позиция вершины 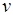является ординарной, frk-позицией либо единственной выходной swh-позицией, которой инцидентно не менее двух информационных дуг. Этот случай соответствует условному ветвлению. Точкой входа в цикл является slt-позиция.

Характер меток входных и выходных позиций определяется семантикой модели вычислений. Напомним, сообщение – вектор, в котором каждый компонент, в свою очередь, представляет собой набор атомарных объектов (значений данных), или токенов. Число входных и выходных позиций вершины графа 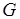совпадает с числом компонентов входного и выходного сообщений соответствующего процесса. Поэтому метка позиции описывает определенные семантические свойства компонента сообщения, а совокупности меток 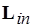, 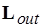характеризуют систему типов сообщений, поддерживаемую моделью вычислений на основе потокового графа .

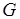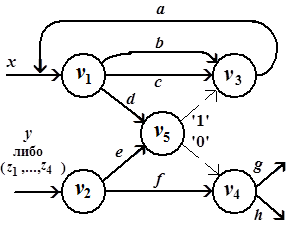
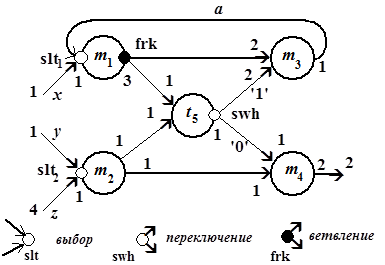
На рис. 2.6, а показан информационно-логический граф программы (информационные связи представлены сплошными дугами, логические– пунктирными), а на рис. 2.6, б приведен соответствующий ему маркированный граф, называемый метаоператорной сетью (М-сетью). Префикс "мета" означает, что здесь мы отвлекаемся от содержательного смысла операторов программы, перенося акцент на взаимодействие процессов, реализующих эти операторы.

 

а)

 

б)

 

Рис. 2.6. Информационно-логический граф (а) и соответствующая М-сеть (б)

 

В информационно-логическом графе (см. рис. 2.6, а) вершины 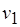- 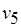соответствуют операторам, которые связаны по данным и управлению (для организации условных ветвлений). Вершина М-сети – метаоператор 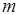, если ее выходные позиции являются ординарными или frk-позициями (на рис. 2.6, б это – метаоператоры 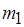- 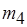). Вершина – тест 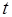, или логическое условие, если она имеет единственную выходную swh-позицию (на рис. 2.6, б это – тест 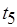). В М-сети метки из 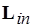, 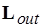– натуральные числа. Метки выходных и входных позиций обозначают число производимых и потребляемых токенов в компонентах соответствующих сообщений. Для описания недетерминированных распределенных вычислений с каждым процессом ассоциируются входные и выходные буферы типа FIFO. Тогда метка позиции обозначает ширину буфера – число токенов в компоненте сообщения. 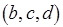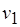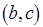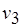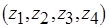Набору операндов, связанных с определенным буфером процесса, например, в , в 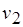, 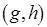в , в 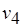, соответствует одна позиция вершины и одна дуга М-сети.

Необходимо сделать несколько замечаний относительно семантики использования позиций альтернативного выбора slt и swh в маркированных потоковых графах, в том числе и в М-сетях. Формально slt-позиция при организации цикла в вычислениях является аналогом булевой функции ИЛИ. Например, процесс, которому соответствует метаоператор 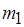(см. рис. 2.6, б), может быть инициирован данными, передаваемыми по дуге 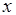. Таким образом, здесь устанавливается приоритет в передаче данных и, соответственно, порядок срабатывания метаоператоров, охваченных циклом. Так, сначала в позицию 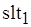метаоператора 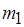данные передаются по дуге 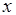, что вызывает срабатывание 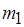, а затем уже возможна передача данных по дуге 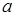после срабатывания метаоператора 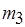. Тем самым гарантируется отсутствие тупиковой ситуации, хотя в рассматриваемой М-сети и существует контур, в который входят вершины 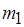и 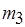. Следовательно, срабатывание метаоператора 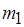обуславливается передачей данных по дуге 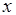или по дуге 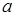. Смысл введения позиции 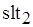в метаоператор 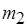иной: соответствующий процесс может начаться, если данные передаются либо только по дуге 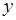, либо только по дуге 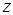. При этом никакого приоритета в передаче данных не предполагается. Следовательно, здесь имеет место аналог булевой функции исключающее ИЛИ. Тест 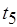передает данные только по дуге '1' метаоператору 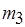, либо только по дуге '0' метаоператору 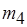. Таким образом, альтернативное переключение swh также является аналогом функции исключающее ИЛИ.

М-сеть охватывает и случай обмена сообщениями между процессами через каналы, или очереди (рис. 2.7), подобно сетям процессов Кана. Длина очереди, или глубина буфера, равна числу входных сообщений. Ширина буфера совпадает с числом токенов в компоненте сообщения. Число очередей (буферов) равно числу компонентов входного сообщения для соответствующего процесса. Так, сообщения для процессов, обозначенных вершинами 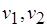являются однокомпонентными, а сообщения процессов, которым соответствуют вершины 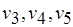– двухкомпонентными. Токены от процесса-производителя пересылаются сразу же, по мере формирования в соответствующие каналы процессов-потребителей. Процесс-потребитель инициируется лишь тогда, когда переданы все необходимые компоненты сообщения от процессов-производителей. Однако при этом, в отличие от детерминированной модели Кана, допускаются различные последовательности формирования токенов в компонентах и самих компонентов входных и выходных сообщений. Дисциплина FIFO строго упорядочивает компоненты входных сообщений, по глубине буферов, а каждый из токенов занимает свое, определенное ему место по ширине соответствующего буфера. Таким образом, сообщение – это двумерный массив, положение любого из токенов в котором однозначно определяется двумя параметрами – принадлежностью к некоторому компоненту и местом в этом компоненте сообщения. Заполнение же этого двумерного массива токенами осуществляется так, что последовательность, в которой токены передаются от процессов-производителей, заранее неизвестна.

 

 

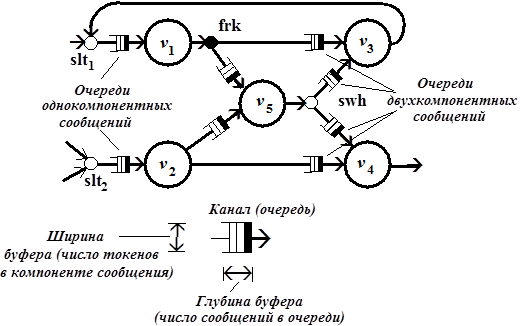
Рис. 2.7. Сеть процессов с очередями

 

Мы уже отмечали, что программную поддержку сложной структуры разнотипных данных, их упорядочение для сохранения целостности сообщений при наличии нескольких буферов у процесса, альтернатив в развитии вычислений целесообразно считать "внутренней" функцией процесса, а не пытаться реализовать ее средствами системы программирования, например, MPI. Системы вроде MPI задают интерфейс, который должен соблюдать пользователь при разработке параллельных программ. В этом смысле функции MPI можно рассматривать как "внешние" по отношению к процессам, обменивающимся сообщениями. Рассмотрим примеры поддержки буферного обмена сообщениями на языке подобном С. Программные средства включают классы очередь (queue) и управляющий буфер (controlFIFO). Очередь сообщений queue описывается такими параметрами, как ширина w и глубина d буфера, а также своим идентификатором iq:

 

queue[w]iq[d];

 

В случае альтернативного выбора информационных потоков (рис. 2.8) описание очередей может быть таким:

 

queue[1]а[da];

queue[1]b[db];

 

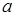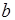Ширина буферов, в которых формируются очереди a и b (им соответствуют дуги и ), определяется меткой входной 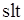-позиции. В общем случае очереди a и b могут иметь различную длину da и db, т.е. содержать различное число сообщений.

 

 

 

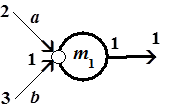
queue[1]a[da];

queue[1]b[db];

queue[w]controlFIFO_m1[d];

/* описание очередей и управляющего буфера */

 

if (!a.empty&&!controlFIFO_m1.full)

controlFIFO_m1.enqueue;

/* постановка на обслуживание сообщений очереди a */

if (!b.empty&&!controlFIFO_m1.full)

controlFIFO_m1.enqueue;

/* постановка на обслуживание сообщений очереди b */

 

Рис. 2.8. Управление альтернативными потоками данных

 

 

Параллельные очереди (рис. 2.9) должны иметь одну и ту же длину d и описываются следующим образом:

 

queue[2]e[d];

queue[1]f[d];

 

 

Ширина параллельных очередей может быть различной.

 

 

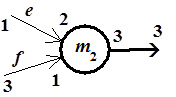
queue[2]e[d];

queue[1]f[d];

queue[w]controlFIFO_m2[d];

/* описание очередей и управляющего буфера */

 

if (!ef.empty&&!controlFIFO_m2.full)

controlFIFO_m2.enqueue;

/* постановка на обслуживание сообщений очередей e, f*/

if (!controlFIFO_m2.empty)

controlFIFO_m2.dequeue;

/* удаление обработанного сообщения из очередей */

 

 

Рис. 2.9. Управление параллельными очередями сообщений

 

Выбор сообщений из очередей процесса p реализуется с помощью управляющего буфера controlFIFO:

queue[w]controlFIFO_p[d];

Его ширина wдолжна быть достаточной для идентификации очереди в альтернативном выборе (см. рис. 2.8) либо нескольких параллельных очередей (см. рис. 2.9). Глубина d управляющего буфера совпадает с длиной соответствующей очереди или параллельных очередей.

Основные методы классов очередь и управляющий буфер:

– опрос очереди и управляющего буфера, которые могут содержать сообщения (.full) либо быть пустыми (.empty);

– постановка на обслуживание (controlFIFO_p.enqueue) и удаление обработанного сообщения из очереди (controlFIFO_p.dequeue).

На рис. 2.8 и 2.9 приведены примеры управления альтернативными и параллельными очередями сообщений.

В общем случае потоковый граф 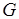соответствует недетерминированной модели вычислений: любой паре, состоящей из входного и выходного сообщений процесса, может соответствовать более одной его истории и допускаются различные последовательности формирования компонентов сообщений. Поясним сказанное. Каждый токен ассоциируется с начальным состоянием входной либо с одним из особых состояний выходной позиции вершины графа 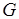, когда осуществляется взаимодействие между процессами программы. Так, формирование метаоператором 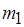любого из трех токенов (см. рис. 2.6, б) вызывает переход процесса в одно из трех особых состояний, или наступление особых событий. Это означает, что связанные с ним процессы (на рис. 2.6, б им соответствуют метаоператор 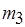и тест 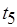) могут перейти в одно из начальных состояний, т.е. могут наступить соответствующие начальные события. Если принимается буферная модель передачи сообщений (см. рис. 2.7), пересылка токенов означает возможность переходов соответствующих входных буферов (на рис. 2.7 – буферов процессов 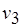и 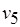) в начальные состояния. Как только будут сформированы токены всех компонентов входных сообщений, инициируются соответствующие процессы. Так, на рис. 2.6, б процесс, обозначаемый метаоператором 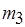, может начаться, получив по два токена в каждую из двух входных позиций от метаоператора 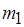и теста .

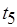Рассмотрим пример иной семантической природы меток входных 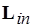и выходных 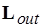позиций вершин графа 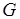. Пусть они обозначают типы компонентов сообщений, или классы токенов, и частично упорядочены. Отношение порядка 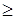представим иерархией наследования типов (рис. 2.10).

В эту иерархию вкладывается следующий смысл: при передаче процессом-отправителем компонента выходного сообщения его тип должен быть "не больше", чем тип компонента соответствующего входного сообщения, принимаемого процессом-получателем. Так, рассмотрим типы double (число с плавающей точкой, или число двойной точности) и int (целое число). (В соответствии с форматом IEEE 754 тип int представляется 32 битами, а double – 64 битами.) Эти типы упорядочены: double 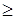int. Положим, процесс 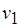(см. рис. 2.7) формирует токены класса int. Тогда классы токенов процессов-потребителей, обозначенные метками соответствующих входных позиций вершин 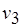и 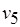, могут, например, иметь типы int или double. Такая семантика меток позволяет ставить вопрос о реализуемости модели вычислений на заданной иерархии классов токенов. Подобная система типов может рассматриваться как основа для реализации концепции полиморфизма при компонентном проектировании программного обеспечения.

Потоковый маркированный граф 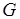адекватно отражает обмен сообщениями с разной структурой: сообщения могут состоять из разнотипных данных, а число (тип) токенов в компоненте выходного сообщения процесса-производителя может не совпадать с числом (типом) токенов компонентов входных сообщений всех процессов-потребителей. Например, на рис. 2.6, б такому обмену соответствует маркировка дуг 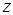, '1', метка frk-позиции метаоператора 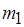, а также метки соответствующих ординарных входных позиций метаоператора 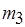и теста .

 

 

 

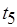Рис. 2.10. Пример иерархии наследования типов данных

 

Связь проблем недетерминизма и блокировки вычислений. Недетерминизм процессов и разнородность сообщений создают опасность блокировки вычислений: процессы-потребители не могут быть инициированы, не имея достаточного количества токенов соответствующих типов во входных буферах от процессов-производителей.

Поясним связь проблем недетерминизма и блокировки вычислений на следующих примерах. Рассмотрим информационно связанные процессы 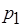, , 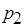, 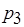взаимодействующие посредством передачи сообщений (рис. 2.11, а). Дуги 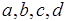соответствуют передаче токенов. Различные структуры сообщений, которыми обмениваются процессы, представим с помощью М-сетей, приведенных на рис. 2.11, б, в, г. Маркировка начал и концов дуг обозначает число токенов в соответствующих компонентах сообщений. Так, выходное сообщение процесса 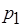состоит из одного компонента 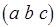– последовательности из трех токенов, передаваемых по дугам 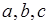. Входное сообщение 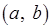метаоператора 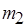на рис. 2.11, б является двухкомпонентным и каждый компонент содержит один токен. Для примеров на рис. 2.11, в, г метаоператору 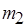передается однокомпонентное сообщение 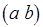– последовательность из двух токенов. На рис. 2.11, б, в входное сообщение 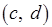, предназначенное метаоператору 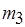, является двухкомпонентным, каждый компонент включает один токен. На рис. 2.11, г показан случай, когда метаоператор 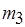получает либо сообщение 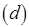, либо сообщение , каждое из которых содержит один компонент и, соответственно, один токен.

 

 

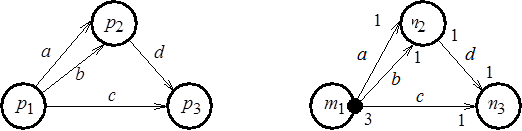
а) б)

 

 

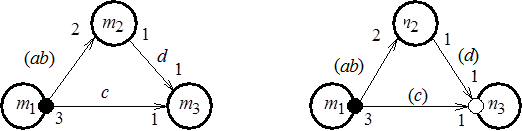
в) г)

 

Рис. 2.11. К проблеме блокировки вычислений

 

Допустим, процесс последовательно формирует три токена, причем возможен произвольный порядок их формирования в выходном сообщении 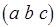(см. рис. 2.11, а), а любой из токенов сообщения 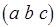является допустимым в компонентах входных сообщений для процессов 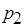, 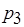. Тогда для примера на рис. 2.11, б существует 6 различных вариантов развития вычислений на одних и тех же для процесса 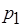входных данных в соответствии с числом 3! возможных перестановок токенов в сообщении 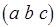. При тех же исходных условиях случай, показанный на рис. 2.11, в, соответствует блокировке вычислений: на любой последовательности токенов в 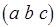метаоператор 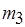может быть инициирован трижды компонентом 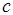и один раз компонентом 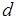сообщения 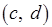, поскольку для срабатывания метаоператора 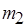необходимо два токена. Процесс же может начаться лишь при наличии всех необходимых входных данных. В примере на рис. 2.11, г возможна альтернатива в вычислениях: метаоператор 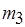инициируется либо сообщением 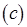, либо сообщением 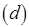. Положим, метаоператоры 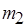и 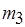"распознают" в сообщении 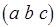предназначенные им токены. Тогда, так же как и в случае на рис. 2.11, б, возможно 6 сценариев развития вычислений на одних и тех же входных данных для процесса 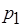. Получение ответа на вопрос о возможности блокировки вычислений, когда метаоператоры 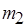, 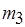(см. рис. 2.11, г) потребляют любой из выходных токенов метаоператора 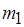, требует специальных методов анализа, которые рассматриваются в разделе 3. То же касается и вопроса, как преобразовать исходную модель обработки (см. например, рис. 2.11, в), чтобы исключить блокировки.

Заметим, что маркировка дуг, подобная используемой в М-сетях, применяется для анализа некоторых разрешимых подклассов потоковых моделей, в частности, и акторных моделей типа SDF. Однако сразу же следует подчеркнуть, что такие модели, как SDF, являются детерминированными моделями вычислений без условных ветвлений и альтернативных слияний потоков данных. Разумеется, и семантическая природа меток в М-сетях иная: по сути, она соответствует числу особых состояний, когда осуществляется обмен данными между процессами, а переход в эти особые состояния случаен.

Таким образом, недетерминированный характер обмена произвольно структурированными данными ставит серьезную задачу анализа реализуемости соответствующей модели обработки, т.е. отсутствия блокировки вычислений при любых допустимых сценариях развития процессов в системе.

Рассмотрим подробнее, каким образом с помощью М-сетей можно интерпретировать возникновение или отсутствие блокировок вычислений при буферном обмене сообщениями. С каждым процессом 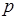программы свяжем 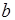входных и 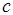выходных буферов сообщений. Входное сообщение представляет собой 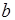-компонентный вектор, 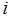-й компонент которого это – набор операндов-аргументов 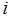-го входного буфера, где 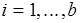. Число аргументов 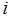-го компонента – ширина 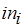буфера, или метка соответствующей входной позиции вершины М-сети. Входные сообщения процесса 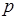образуют очередь, длина 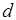которой является глубиной всех 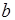буферов. В каждый из входных буферов процесса 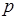операнды-результаты соответствующих процессов поступают асинхронно, при этом буфер (процесс) переходит в одно из начальных состояний. Процесс 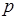инициируется после формирования полного сообщения из 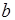наборов аргументов. Таким образом, входная очередь – это массив из 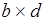наборов аргументов, а 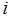-й буфер хранит массив из 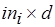аргументов, где 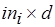может рассматриваться как метка входящей дуги в М-сети. Выходное сообщение процесса представляет собой 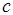-компонентный вектор, 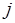-й компонент которого это – набор операндов-результатов 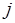-го выходного буфера, где 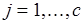. Число результатов 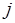-го компонента сообщения – ширина 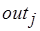буфера, или метка соответствующей выходной позиции вершины М-сети. Каждому входному сообщению процесса 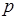соответствует выходное сообщение, так что выходная очередь это – массив из 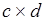наборов результатов, при этом в 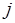-м буфере хранится массив из 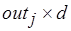результатов, где 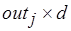может рассматриваться как метка исходящей дуги М-сети. Глубина 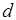входных и выходных буферов процесса 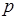может присваиваться как метка соответствующей вершине М-сети. Формирование промежуточных и окончательных результатов вычислений происходит асинхронно и появление любого из них переводит выходной буфер (процесс) в одно из особых состояний. Условные ветвления реализуются процессами с одним выходным буфером, который может находиться в одном из заключительных состояний, причем ему соответствует определенное значение