Метод аналитической аппроксимации основан на замене характеристики (или ее участка) нелинейного элемента общим аналитическим выражением. Применяются следующие виды аналитической аппроксимации:
· степенным многочленом (см. рис. 2,а);
· трансцендентными (экспоненциальными, гиперболическими и др.) функциями (см. рис. 2,б).
Выбор коэффициентов (а,b,c,…) осуществляется исходя из наибольшего соответствия аналитического выражения рабочему участку нелинейной характеристики. При этом
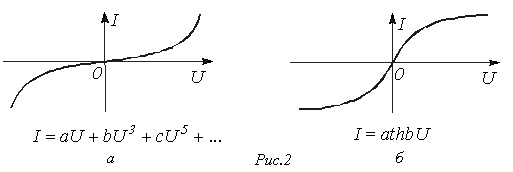
выбираются наиболее характерные точки, через которые должна пройти аналитическая кривая. Число точек равно числу коэффициентов в аналитическом выражении, что позволяет однозначно определить последнее.
Необходимо помнить, что при получении нескольких корней нелинейного уравнения они должны быть проверены на удовлетворение задаче. Пусть, например, в цепи, состоящей из последовательно соединенных линейного R и нелинейного резисторов, ВАХ последнего может быть аппроксимирована выражением 
. Определить ток в цепи, если источник ЭДС Е обеспечивает режим работы цепи в первом квадранте.
В соответствии со вторым законом Кирхгофа для данной цепи имеет место уравнение
или
.
Корни уравнения
.
Решением задачи является 
, поскольку второе решение 
не удовлетворяет условиям исходя из физических соображений.
Метод линеаризации применим для анализа нелинейных цепей при малых отклонениях рабочей точки Р (см. рис. 5) от исходного состояния.
В окрестности рабочей точки 
(см. рис. 5)
,
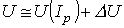где 
(закон Ома для малых приращений);
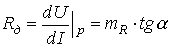-дифференциальное сопротивление.
Идея метода заключается в замене нелинейного резистора линейным с сопротивлением, равным дифференциальному в заданной (или предполагаемой) рабочей точке, и либо последовательно включенным с ним источником ЭДС, либо параллельно включенным источником тока. Таким образом, линеаризованной ВАХ (см. прямую на рис. 5) соответствует последовательная (рис. 6,а) или параллельная (рис. 6,б) схема замещения нелинейного резистора.
|
|
Если исходный режим определен и требуется рассчитать лишь приращения токов и (или) напряжений, обусловленные изменением напряжения или тока источника, целесообразно использовать эквивалентные схемы для приращений, получаемые на основании законов Кирхгофа для малых приращений:
-первый закон Кирхгофа: 
;
-второй закон Кирхгофа: 
.
При составлении схемы для приращений:
1) все ЭДС и токи источников заменяются их приращениями;
2) нелинейные резисторы заменяются линейными с сопротивлениями, равными дифференциальным в рабочих точках.
Необходимо помнить, что полная величина какого-либо тока или напряжения в цепи равна алгебраической сумме исходного значения переменной и ее приращения, рассчитанного методом линеаризации.
Если исходный режим работы нелинейного резистора неизвестен, то следует задаться рабочей точкой на его ВАХ и, осуществив соответствующую линеаризацию, произвести расчет, по окончании которого необходимо проверить, соответствуют ли его результаты выбранной точке. В случае их несовпадения линеаризованный участок уточняется, расчет повторяется и так до получения требуемой сходимости