ДИСТАНЦИОННОЕ ОБУЧЕНИЕ
Урок Лекция-практика Логарифмические неравенства их типы и методы
Решения.
Цели: рассмотреть типы логарифмических неравенств и методы их решения.
При решении логарифмических неравенств надо хорошо знать свойства логарифмической функции 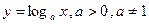 .
.
| Свойства функции | 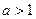
| 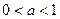
| |
| 1. | Область определения | 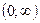
| |
| 2. | Область значений | 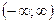
| |
| 3. | Четность, нечетность | Функция не является ни четной, ни нечетной | |
| 4. | Нули функции | 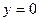 при при 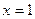
| |
| 5. | Промежутки знакопостоянства | 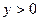 при при 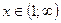
 при при 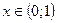
| 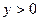 при при 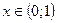
 при при 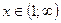
|
| 6. | Экстремумы | Функция экстремумов не имеет | |
| 7. | Промежутки монотонности
при 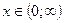
| Функция возрастает | Функция убывает |
Рассмотрим взаимное расположение графика функции 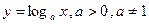 и прямой
и прямой 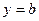 .
.

| 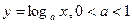
|
| 
|
Вывод. Прямая 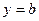 пересекает график функции
пересекает график функции 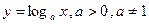 в единственной точке
в единственной точке 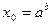 .
.
Определение. Пусть 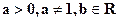 , тогда неравенства
, тогда неравенства 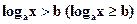 или
или 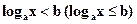 называются простейшими логарифмическими неравенствами.
называются простейшими логарифмическими неравенствами.
Что значит решить неравенство?
Решить неравенство - значит, найти все его решения или показать, что их нет.
Что называется решением неравенства?
Решением неравенства с неизвестным 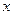 называют число
называют число 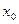 , при подстановке которого в неравенство вместо
, при подстановке которого в неравенство вместо 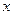 получается верное числовое неравенство.
получается верное числовое неравенство.
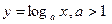
| |

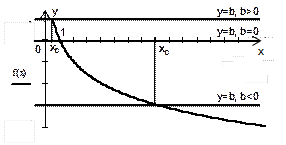
| Вывод. Если 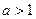 , то для каждого , то для каждого 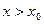 соответствующая точка графика функции соответствующая точка графика функции  находится выше прямой находится выше прямой 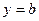 , а для каждого , а для каждого 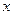 из интервала из интервала 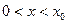 соответствующая точка графика функции соответствующая точка графика функции  находится ниже прямой находится ниже прямой 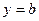 . .
|
Вывод 1:
Основание логарифма 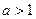
| |
Вид уравнения:
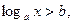 Переходим к равносильной системе
Переходим к равносильной системе
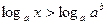 И решаем неравенство:
И решаем неравенство:
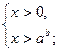 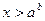 . .
| Вид уравнения
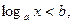 Переходим к равносильной системе
Переходим к равносильной системе
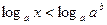 ,
И решаем неравенство ,
И решаем неравенство
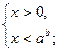 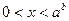 . .
|
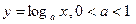
| |
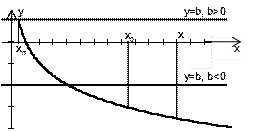
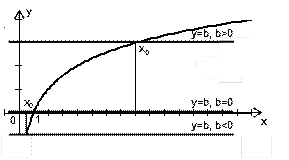
| Вывод. Если 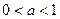 , то для каждого , то для каждого 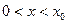 соответствующая точка графика функции соответствующая точка графика функции 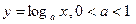 находится выше прямой находится выше прямой 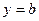 , а для каждого , а для каждого 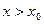 соответствующая точка графика функции соответствующая точка графика функции 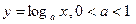 находится ниже прямой находится ниже прямой 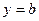 . .
|
Вывод 2:
Основание логарифма 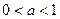
| ||
Вид уравнения
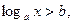 Переходим к равносильной системе
Переходим к равносильной системе
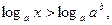 И решаем неравенство
И решаем неравенство
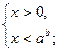 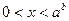 . .
| Вид уравнения
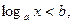 ,
Переходим к равносильной системе ,
Переходим к равносильной системе 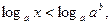 И решаем неравенство
И решаем неравенство
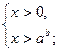 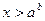 . .
|
Типы логарифмических неравенств и методы их решения.
Простейшие логарифмические неравенства.
Пример 1. 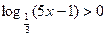 .
.
Решение:
Т. к. Область определения функции 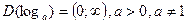 ;
; 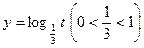 убывает на всей области определения и
убывает на всей области определения и 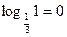 , то неравенство равносильно системе
, то неравенство равносильно системе
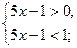
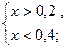
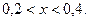
Ответ: (0,2;0,4).
Пример 2. 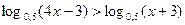 .
.
Решение:
Т. к. Область определения функции 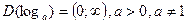 ;
; 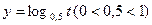 убывает на всей области определения, то неравенство равносильно системе
убывает на всей области определения, то неравенство равносильно системе
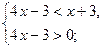
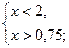
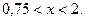
Ответ: (0,75;2).
2). Логарифмические неравенства, сводящиеся к простейшим логарифмическим неравенствам.
Пример 1. 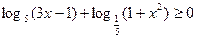 .
.
Решение:
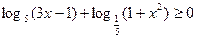 ,
,
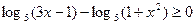 ,
,
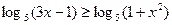 .
.
Т. к. Область определения функции 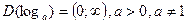 и
и 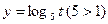 возрастает на всей области определения, то неравенство равносильно системе
возрастает на всей области определения, то неравенство равносильно системе
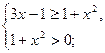 т. к.
т. к. 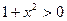 , при
, при 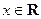 , то система равносильна неравенству
, то система равносильна неравенству 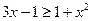 .
.
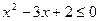 ,
,
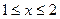 .
.
Ответ: 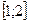 .
.
Пример 2. 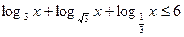 .
.
Решение:
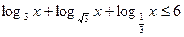 ,
,
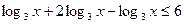 ,
,
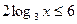 ,
,
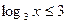 .
.
Т. к. Область определения функции 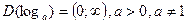 ;
; 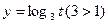 возрастает на всей области определения и
возрастает на всей области определения и 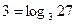 , то неравенство равносильно системе
, то неравенство равносильно системе
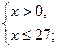
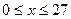 .
.
Ответ: 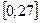 .
.
Пример 3. 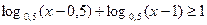 .
.
Решение:
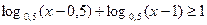 .
.
Т. к. Область определения функции 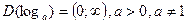 ;
; 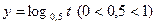 убывает на всей области определения и
убывает на всей области определения и 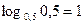 , то неравенство равносильно системе
, то неравенство равносильно системе
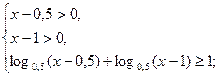
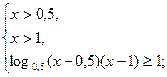
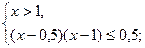
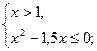
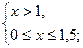
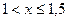 .
.
Ответ: 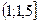 .
.
Пример 4. 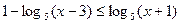 .
.
Решение:
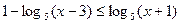 .
.
Т. к. Область определения функции 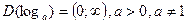 ;
; 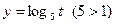 возрастает на всей области определения и
возрастает на всей области определения и 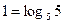 , то неравенство равносильно системе
, то неравенство равносильно системе
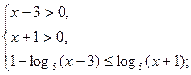
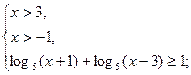
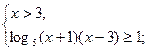
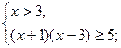
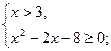
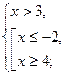
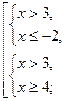
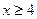 .
.
Ответ: 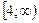 .
.
3). Логарифмические неравенства, сводящиеся к неравенствам второй степени.(Метод замены переменной и приведение к квадратному неравенству)
Пример 1. 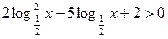 .
.
Решение:
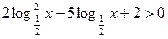 . Пусть
. Пусть 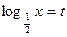 тогда
тогда
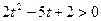 ,
,
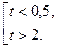
Вернёмся к переменной 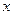 . Т. к. Область определения функции
. Т. к. Область определения функции 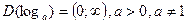 , то
, то
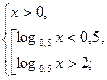
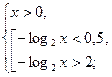
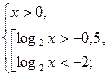
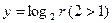 возрастает на всей области определения, то
возрастает на всей области определения, то
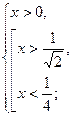
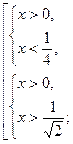
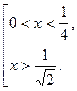
Ответ: 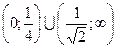 .
.
Пример 2. 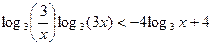 .
.
Решение:
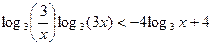 .
.
Т. к. Область определения функции 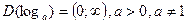 , то для нахождения области допустимых значений переменной
, то для нахождения области допустимых значений переменной 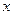 составим систему:
составим систему:
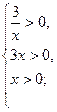
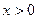 .
.
В найденной области допустимых значений переменной 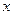 преобразуем неравенство.
преобразуем неравенство.
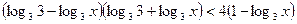 ,
,
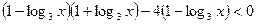 ,
,
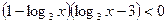 ,
,
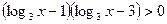 ,
,
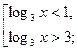
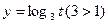 возрастает на всей области определения и
возрастает на всей области определения и 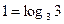 , а также
, а также 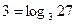 .
.
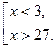
С учётом области допустимых значений переменной 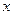 получим:
получим:
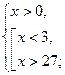
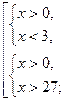
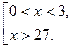
Ответ: 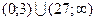 .
.