Лекция
ТЕНИ
Общие положения
Тени показывают на ортогональных, аксонометрических и перспективных проекциях различных строительных конструкций, зданий и сооружений для придания большей наглядности и рельефности их изображениям. Чертежи пространственных фигур с нанесенными на них тенями позволяют более определенно судить об их взаимном расположении в пространстве, о форме их отдельных фрагментов.
Теоретические основы построения теней
Предметы в окружающей среде освещаются либо лучами солнца, либо другими источниками света. Если светящаяся точка находится на конечном расстоянии от объекта – освещение называется факельным, если удалена в бесконечность – солнечным.
Тени, придающие плоским чертежам большую выразительность, разделяют на собственные и падающие.
Пусть источник света (солнце), освещая какой-либо геометрический объект (например, шар), удален в бесконечность в направлении, противоположном S. Тогда световые лучи, идущие от источника, будут параллельны друг другу. Множество лучей, упирающихся в поверхность шара, образуют световой цилиндр. Оболочка цилиндрической поверхности, касаясь шара, отделит освещенную поверхность шара от неосвещенной.

Рис. 7.1 Механизм получения собственных и падающих теней
Поскольку цилиндрическая поверхность, образованная световыми лучами, соосна со сферой, ограничивающей шар, – общим элементом для обеих поверхностей будет окружность, за которой поверхность шара не освещается. За окружностью находится теневой цилиндр. Образованная множеством световых лучей цилиндрическая поверхность называется проецирующей.
Граница между освещенной и неосвещенной частями поверхности предмета – контур собственной тени.
Собственная тень объекта проецирования – это совокупность неосвещенных элементов поверхности предмета.
В рассматриваемом случае объектом освещения был шар, следовательно, множество световых (проецирующих) лучей образовали поверхность кругового цилиндра. Последняя, являясь поверхностью 2-го порядка, пересечется с плоскостью проекций Р по эллипсу, который представляет собой падающую тень шара. Поэтому падающая тень – это тень, отбрасываемая предметом на другой предмет или на какую-либо плоскость (в том числе и на плоскость проекций) или поверхность (рис.7.1). Следовательно, в случае бесконечно-удаленного источника света тень – это параллельная косоугольная проекция предмета.
За направление лучей света обычно принимают направление одной из диагоналей куба, грани которого параллельны плоскостям проекций. Такой куб называется световым, а его проекции — световыми квадрантами (рис.7.2).
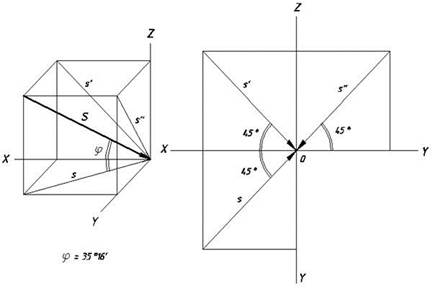
Рис. 7.2. Световой куб и световые квадранты
Тень от точки
Рассмотрим построение тени точки в ортогональных проекциях. Пусть даны чертежи двух точек А (рис.7.3). Проведем в пространстве световой луч через точку А (а, а'). Фронтальная проекция луча пройдет через точку а', а горизонтальная –через точку а на основании свойства параллельных проекций.
аТ – действительная тень точки А на плоскости Н;
аТ' – действительная тень точки А на плоскости V.
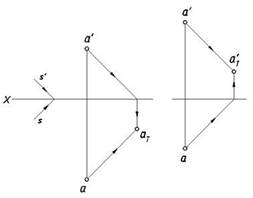
Рис. 7.3. Построение теней точки на плоскостях проекций
Из приведенных рассуждений можно сделать вывод: тень точки падает на ту плоскость проекций, к которой точка расположена ближе.
Заметим, что плоскости проекций считаются непрозрачными, поэтому действительная тень точки А может получиться только на одной из них. При мысленном продолжении луча его пересечение произойдет и с другой плоскостью проекций, на которой получится мнимая (фиктивная) тень точки (рис. 7.4). Обозначим эти тени следующим образом:
аТ(ф) — мнимая тень точки А на плоскости Н;
аТ'(ф) — мнимая тень точки А на плоскости V.
Конечно, в реальной жизни мнимых теней не бывает, но для решения практических геометрических задач их используют довольно часто.
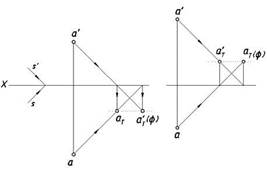
Рис. 7.4. Построение мнимых теней точки
Тень от плоских фигур
До сих пор нами рассматривались геометрические образы, у которых могли быть только падающие тени. У фигур, ограниченных плоскими отсеками, наряду с падающими тенями будут существовать и собственные, поскольку плоскость – двусторонняя поверхность.
Рассмотрим отсеки плоских фигур (треугольника и круга), соответственно параллельные плоскостям V и H. Очевидно, что при заданном направлении светового потока, неосвещенные стороны отсеков плоскостей на соответствующих проекциях будут закрыты оригиналами.
Совокупность сторон треугольника представляет собой контур собственной тени. Лучевые плоскости, проходящие через стороны треугольника, образуют призматическую поверхность, которая, пересекая плоскость V, образует на ней фигуру, равную данному треугольнику, поскольку (ABC)% V. Построение падающей тени треугольного отсека показано на рис.7.5.
На основании этих построений можно сделать вывод: граница падающей тени плоской фигуры является тенью от контура собственной тени этой фигуры.
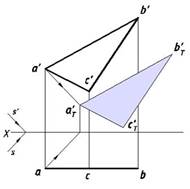
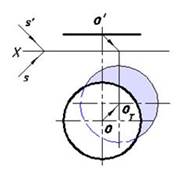
Рис.7.5 Падающая тень треугольника Рис. 7.6. Падающая тень круга
Множество световых лучей, проходящих через каждую точку окружности другого плоского отсека, образуют поверхность эллиптического цилиндра, которая пересекает плоскость H по окружности.
Окружность-оригинал и падающую тень круга на плоскости H можно считать параллельными сечениями светового эллиптического цилиндра. Для нахождения местоположения падающей тени следует определить действительную тень центра данного круга на плоскости H (рис.7.6).
Тени от геометрических поверхностей
Тень от призмы
Пусть дана прямая призма, стоящая на плоскости H. Требуется построить ее собственные и падающие тени на плоскости проекций H и V. (рис.7.6). Проанализируем освещенность граней. При заданном направлении светового потока будут освещены верхняя и левая передняя грань. Остальные грани (в том числе и нижняя) находятся в тени. Для построения падающей тени объемного тела необходимо выявить контур собственной тени, который в данном случае будет представлять собой пространственную ломаную линию. Элементами этой линии являются ребра призмы, находящиеся на границах освещенных и неосвещенных плоскостей. На этом же рисунке представлено изометрическое изображение замкнутого контура собственной тени, от которого построена падающая тень.
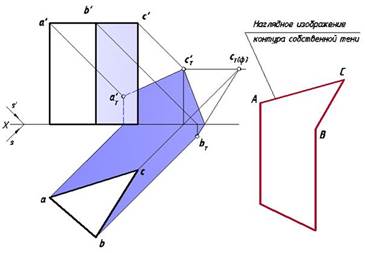
Рис. 7.6 Построение собственных и падающих теней призмы
Тень от цилиндра
Контур собственной тени цилиндра определяется двумя образующими, по которым лучевые плоскости касаются его боковой поверхности. Для нахождения контура падающей тени необходимо построить тени этих образующих и тень от верхнего основания цилиндра (рис.7.7).
Тень от конуса
При построении тени конуса сначала строят падающую тень, с помощью которой затем определяют контур собственной тени (рис.7.8).
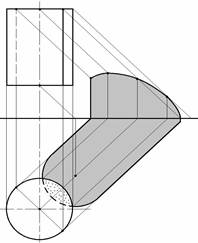 |  | ||
Рис.7.7 Рис.7.8
Более подробно с данной темой можно ознакомиться в методическом пособии О.В. Георгиевского «Построение теней в ортогональных, перспективных и аксонометрических проекциях», имеющееся в библиотеке.