1. Основные сведения из динамики АСР
1.1. Переходный процесс в АСР

При нормальных условиях эксплуатации вся система регулирования находится в установившемся режиме. При этом все регулируемые величины соответствуют своим номинальным значениям, а регулирующие органы неподвижны. Такой режим работы АСР называют статическим. Если в какой-то момент времени к системе приложено какое-то возмущение (f(t)), то это приведет к отклонению регулируемых величин от заданных значений и, как следствие, к работе регулирующих устройств с целью устранения причин возмущения и возвращения регулируемых величин к своим номинальным или близким к ним значениям.
Изменение регулируемых величин во времени в течение всего процесса регулирования называют переходным процессом.
Такой режим работы системы называют динамическим режимом (динамикой).
В общем случае динамика в линейной непрерывной АСР может быть описана линейным неоднородным дифференциальным уравнением с постоянными коэффициентами.

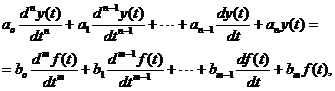

где
 - постоянные коэффициенты;
- постоянные коэффициенты;
y(t) - регулируемая величина;
f(t) - возмущающее воздействие.
Эта запись предполагает зависимость выходной величины y(t) от входного воздействия f(t) и независимость входного воздействия f(t) от выходного сигнала
y(t) (Рис. 1.1.).
f(t) y(t)
 |
Рис. 1.1.
Полагая 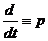 , т.е. вводя символ дифференцирования
, т.е. вводя символ дифференцирования 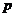 , уравнение можно записать в виде:
, уравнение можно записать в виде:
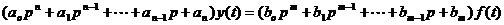
или
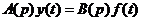 .
.
Здесь 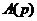 и
и 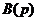 - операторные многочлены левой и правой частей уравнения.
- операторные многочлены левой и правой частей уравнения.
Общее решение линейного неоднородного дифференциального уравнения ищется в виде двух слагаемых - вынужденного движения ув и свободных
колебаний усв(t):
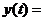 ув + усв(t).
ув + усв(t).
Вынужденная составляющая переходного процесса является установившимся значением регулируемой величины и находится из исходного дифференциального уравнения приравниванием к нулю всех производных в левой и правой частях уравнения.
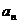 ув=
ув=  уст, т.е. ув=
уст, т.е. ув= 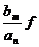 уст
уст
Свободная составляющая переходного процесса (усв 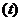 ) или, иначе, переходная составляющая (упер
) или, иначе, переходная составляющая (упер 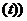 общего решения неоднородного дифференциального уравнения ищется как общее решение однородного дифференциального уравнения в виде:
общего решения неоднородного дифференциального уравнения ищется как общее решение однородного дифференциального уравнения в виде:
усв 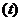 =упер
=упер 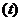 =
= 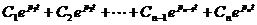 =
= 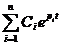 ,
,
где
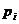 - і-ый корень характеристического уравнения
- і-ый корень характеристического уравнения 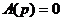 ,
,
соответствующего однородному дифференциальному уравнению:
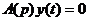 ;
;
 - і-ая постоянная интегрирования, определяемая из начальных условий;
- і-ая постоянная интегрирования, определяемая из начальных условий;
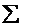 - символ суммирования отдельных составляющих общего решения.
- символ суммирования отдельных составляющих общего решения.
Начальными условиями называют значения функций и их производных до 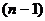 го порядка включительно при
го порядка включительно при 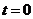 (в начальный момент времени).
(в начальный момент времени).
Различают начальные условия для моментов времени  и
и 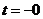 .
.
В первом случае рассматривается поведение функции в нулевой момент времени сразу же после приложения возмущения (справа от начала координат); второй случай - поведение функции в нулевой момент времени, непосредственно перед приложением возмущающего воздействия (слева от начала координат).
Устойчивость АСР
Переходный процесс в системе описывается уравнением:
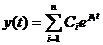
Если все корни простые действительные (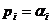 ), то каждая из составляющих переходного процесса изменяется по закону экспоненты.
), то каждая из составляющих переходного процесса изменяется по закону экспоненты.
 При этом переходная составляющая процесса стремится к нулю при
При этом переходная составляющая процесса стремится к нулю при 
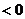 (рис.1.2 а) или уходит в бесконечность от установившегося значения при
(рис.1.2 а) или уходит в бесконечность от установившегося значения при  (рис.1.2 б).
(рис.1.2 б).

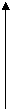 y y
y y
 |


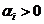

 0 t 0 t
0 t 0 t
а) б)
Рис. 1.2
Если в уравнении имеется комплексный сопряженный корень  ,то соответствующая ему составляющая переходного процесса изменяется по синусоидальному закону (рис.1.3):
,то соответствующая ему составляющая переходного процесса изменяется по синусоидальному закону (рис.1.3):
 ,
,
где
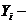 амплитуда колебаний;
амплитуда колебаний;
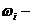 частота колебаний;
частота колебаний;
 сдвиг фаз (начальная фаза).
сдвиг фаз (начальная фаза).
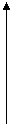
 y y
y y
ai<0 ai>0 


 0 t 0 t
0 t 0 t
а) б)
Рис.1.3.
Эти величины играют роль постоянных интегрирования. При этом 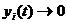 при
при 
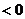 (рис.1.3 а) и уходит в бесконечность при
(рис.1.3 а) и уходит в бесконечность при  (рис.1.3. б).
(рис.1.3. б).
АСР, переходные процессы в которых ²затухают ² с течением времени, называют устойчивыми.
АСР, у которых переходные процессы расходятся с течением времени, называют неустойчивыми.
Работоспособные системы должны быть устойчивыми.
Из изложенного вытекает необходимое условие устойчивости системы -отрицательность действительной части корней характеристического уравнения, соответствующего дифференциальному уравнению, которым описывается динамика системы.
1.3. Принцип суперпозиции. Типовые возмущения.
Для линейной системы справедлив принцип суперпозиции, заключающийся в том, что сумме любых возмущений соответствует сумма выходных реакций, каждая из которых определяется соответствующим воздействием; при любом изменении входного возмущения без изменения его формы выходная величина претерпевает такое же изменение, также не изменяя формы.
Принцип суперпозиции применим не только к суммам, но и к интегралам. Если входное возмущение в системе представляет собой бесконечно большое число бесконечно малых элементарных возмущений, то выходная величина линейной системы представляет собой сумму бесконечно малых реакций на эти бесконечно малые возмущения.
Принцип суперпозиции дает возможность выразить реакцию системы на любое возмущение через ее реакцию на определенный вид элементарных возмущений. Для этого достаточно представить произвольное возмущение элементарными воздействиями выбранного типа.
В качестве типовых возмущений чаще всего применяют единичную скачкообразную функцию, единичную импульсную функцию, единичную линейную функцию, единичное гармоническое колебание.
1. Единичная скачкообразная функция описывает мгновенное изменение какого-то воздействия от 0 до 1 (рис.1.4).
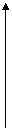 f
f
 |
t
 0 t
0 t
Рис.1.4.
Аналитически скачкообразную функцию записывают как:
 0 при
0 при 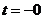 и
и 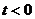
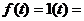
1 при 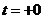 и
и 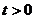
2. Единичная импульсная функция описывает кратковременное возмущение, имеющее характер кратковременного импульсного толчка (рис. 1.5).
 f
f
 |

 0 t
0 t
Рис.1.5.
Единичная импульсная функция, называемая 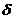 - функцией Дирака, представляет собой первую производную от единичной скачкообразной функции:
- функцией Дирака, представляет собой первую производную от единичной скачкообразной функции:
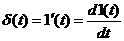
и равна нулю везде, кроме 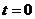 , где она принимает бесконечное значение, причем при условии, что интеграл от нее по любому интервалу, содержащему
, где она принимает бесконечное значение, причем при условии, что интеграл от нее по любому интервалу, содержащему 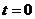 , равен единице.
, равен единице.

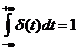
Функцию, обладающую такими свойствами, можно получить как предел положительного прямоугольного импульса, имеющего единичную площадь, когда длительность этого импульса стремится к нулю (рис. 1.6).
 f
f







 S(=1)
S(=1) 

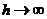
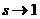
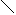 h
h
 t
t
0
Рис.1.6.
3. Единичную линейную функцию  при
при 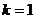 называют еще рамповым возмущением (Рис. 1.7).
называют еще рамповым возмущением (Рис. 1.7).
 f
f 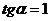
 |


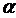
0 t
Рис.1.7.
Такое возмущение является типичным для следящих систем регулирования.
4. Единичное гармоническое возмущение чаще всего записывают как функцию, изменяющуюся по синусоидальному закону (Рис. 1.8):
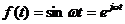
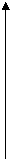 |
f 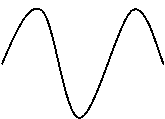
 |

 0 t
0 t
 |
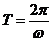
Рис. 1.8
Такой тип возмущений применяют при частотных методах анализа АСР.
2. ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЙ ЛАПЛАСА В ТАУ
2.1. Прямое и обратное преобразования Лапласа
Уравнения динамики АСР в символической Форме имеют вид:
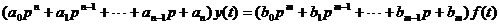 ,
, 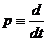
или
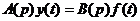 .
.
Для нахождения интеграла функции 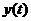 нужно решить характеристическое уравнение:
нужно решить характеристическое уравнение:
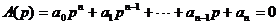
Уравнения пятой и выше степеней в радикалах не решаются, а решения уравнений третьей и четвертой степеней громоздки. Поэтому при анализах АСР переходят от классических методов решения дифференциальных уравнений к их решениям с помощью преобразований Лапласа.
Преобразование Лапласа – функциональное преобразование, при котором функция вещественного переменного 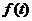 преобразуется в функцию комплексного
преобразуется в функцию комплексного
переменного  .
.
Функция 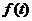 преобразуема по Лапласу, если она определена и однозначна для всей области
преобразуема по Лапласу, если она определена и однозначна для всей области  и если
и если
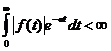 (конечен),
(конечен),
т.е. если она удовлетворяет условиям Дирихле.
Минимум значения  , при котором указанный интеграл конечен, называют абсциссой абсолютной сходимости. Для большинства функций
, при котором указанный интеграл конечен, называют абсциссой абсолютной сходимости. Для большинства функций  =0. Функцию
=0. Функцию 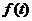 называют оригиналом. Функцию
называют оригиналом. Функцию  - изображением (по Лапласу).
- изображением (по Лапласу).
Преобразование оригинала в изображение называют прямым преобразованием Лапласа и осуществляют с помощью интеграла:
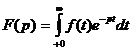
Преобразование изображения в оригинал называют обратным преобразованием Лапласа и осуществляют с помощью интеграла:
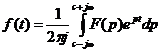 ,
,
Операции прямого и обратного преобразований Лапласа будем обозначать через L и L-1 соответственно.
Связь между оригиналом и изображением записывается в виде:
 .
.
Пример 1. Найти изображение единичной скачкообразной функции 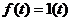 .
.
L 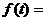 L
L 
 .
.
Пример 2. Найти изображение показательной функции  .
.
L 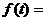 L
L 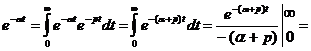
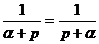 ;
;
2.2. Основные теоремы преобразования Лапласа
2.2.1. Теоремы линейности
L 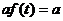 L
L 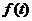 ,
, 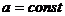 ,
,
L  L
L 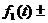 L
L 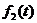 .
. 
2.2.2. Теоремы о конечном и начальном значениях оригинала
 ,
,
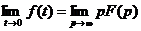 .
.
2.2.3. Теорема запаздывания в области вещественного переменного.
Если функция 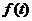 смещена на величину t от начала координат (Рис. 2.1.), то такую функцию называют функцией с запаздывающим аргументом и записывают как
смещена на величину t от начала координат (Рис. 2.1.), то такую функцию называют функцией с запаздывающим аргументом и записывают как  .
.
 f
f

 0
0 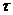
 t
t

Рис.2.1.
Изображение такой функции имеет вид:
L 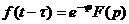 .
.
2.2.4. Теорема смещения в области комплексного переменного.
L 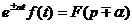 ,
,
где  - величина смещения в комплексной плоскости.
- величина смещения в комплексной плоскости.
2.2.5. Теоремы масштабов
L  ,
, 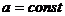
L 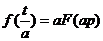 ,
, 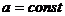
2.2.6. Теорема дифференцирования при нулевых начальных условиях
L 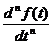
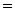 L
L 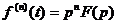 ,
,
где n-порядок производной.
2.2.7. Теорема интегрирования при нулевых начальных условиях
L 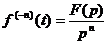 ,
,
Здесь n-кратность интеграла.
2.2.8. Теорема свертки оригиналов
Если
 и
и 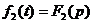
то
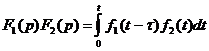 ,
,
где t-переменная интегрирования.
2.3. Передаточная функция
Динамику АСР относительно регулируемой величины 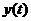 по каналу возмущающего воздействия
по каналу возмущающего воздействия 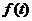 можно записать в виде дифференциального уравнения в символической форме:
можно записать в виде дифференциального уравнения в символической форме:
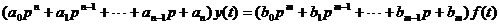 ,
, 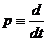
или
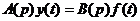
Если это уравнение преобразовать по Лапласу, используя теоремы линейности и дифференцирования при нулевых начальных условиях, то преобразованное по Лапласу уравнение по форме записи будет совпадать с символичной формой. Отличие заключается в том, что вместо оригиналов 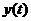 и
и 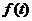 нужно записывать их изображения
нужно записывать их изображения 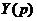 и
и  и под символом дифференцирования
и под символом дифференцирования 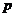 понимать комплексную переменную. С учетом сказанного, преобразованное по Лапласу при нулевых начальных условиях исходное уравнение динамики примет вид:
понимать комплексную переменную. С учетом сказанного, преобразованное по Лапласу при нулевых начальных условиях исходное уравнение динамики примет вид:
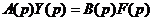 ,
,
где
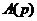 и
и 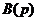 -операторные многочлены левой и правой частей уравнения,
-операторные многочлены левой и правой частей уравнения,
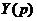 и
и  -изображения выходной и входной величин.
-изображения выходной и входной величин.
Последнее выражение можно записать в виде
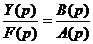
Отношение изображения выходной величины системы к изображению входного воздействия при нулевых начальных условиях называют передаточной функцией системы.
Обычно, эту функцию записывают как
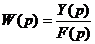
2.4. Переходный процесс в АСР
Изображение 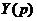 регулируемой величины
регулируемой величины 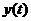 , т.е. изображение переходного процесса можно выразить через передаточную функцию
, т.е. изображение переходного процесса можно выразить через передаточную функцию 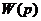 системы относительно регулируемой величины
системы относительно регулируемой величины 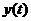 по каналу возмущающего воздействия
по каналу возмущающего воздействия 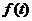 как:
как:
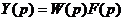 ,
,
где  -изображение возмущающего воздействия.
-изображение возмущающего воздействия.