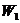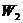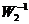ЛИНЕЙНЫЕ НЕПРЕРЫВНЫЕ АСР 6 глава

6.3.1. Корректирующая обратная связь

 

П и И – регуляторы не всегда обеспечивают надлежащее качество регулирования.

П – регулятор предопределяет статизм системы и в связи с этим могут возникать случаи, когда статическая ошибка превышает допустимое ее значение. В связи с этим появляется необходимость введения корректирующих устройств, устраняющих приведенные недостатки простейших регуляторов.

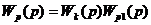Если закон регулирования определяется передаточной функцией а желателен то и

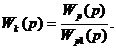
В большинстве случаев при формировании законов регулирования, отличных от простейших, коррекции осуществляются с помощью обратной связи по двум типам структурных схем, когда обратная связь охватывает только усилитель (рис. 6.1) и когда обратная связь охватывает и усилитель и исполнительный механизм (рис. 6.2).

 

y_з(t) + у_р(t)

ЧЭ У ИМ

-

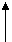ОС

 

Рис.6.1.

 

y_з(t) + у_р(t)

ЧЭ У ИМ

-

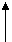ОС

 

Рис.6.2.

 

Контур с обратной связью является предельной системой.

В этом случае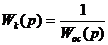

Следовательно,

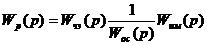
и

.

Чувствительный элемент относят к объекту управления, исключая из структурной схемы регулятора, в связи с тем, что динамические свойства ЧЭ отражены в характеристике объекта управления.

Тогда

для случая, когда обратная связь охватывает только усилитель,

и

для случая охвата обратной связью и усилителя и исполнительного механизма.

Таким образом, для получения желаемого закона регулирования при введении коррекции по типу обратной связи передаточные функции устройств обратной связи определяются как:

и

.

 

 

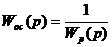6.3.2. Пропорционально-интегральный (ПИ) закон регулирования

 

В этом случае

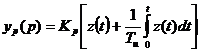
Постоянную интегрирования Т_и называют временем изодрома.

 

Преобразуем уравнение по Лапласу

.

Отсюда

Подставив р= , получим АФХ регулятора

где

А_рПИ

График АФХ приведен на рисунке 6.3.

K_p

₀

 

 

 

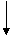
Рис.6.3.

 

Переходная функция регулятора:

График переходной функции приведен на рисунке 6.4.

h_рпн

 

 

K_p

⁰ t

 

Рис.6.4.

 

Обычно ПИ-регулятор реализуют с помощью обратной связи.

Если обратная связь охватывает только усилитель, то передаточная функция обратной связи принимает вид:

Если исполнительный механизм является интегрирующим звеном с передаточной функцией

,

то

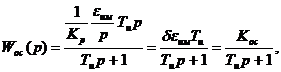
где

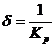- степень обратной связи;

- коэффициент передачи звена обратной связи.

Следовательно, обратная связь должна быть выполнена в виде апериодического звена первого порядка. Такую обратную связь называют жесткой обратной связью с инерционностью первого порядка.

Если обратная связь охватывает и усилитель и исполнительный механизм,

то

Следовательно, обратная связь должна быть выполнена в виде реального дифференцирующего звена. Такую обратную связь называют упругой или гибкой обратной связью.

Вообще жесткой обратной связью называют такую, которая в установившемся режиме работы пропускает установившееся значение входного воздействия.

Гибкой обратной связью называют обратную связь, которая в установившемся режиме не пропускает установившегося значения входного сигнала.

Обязательным элементом гибкой обратной связи является дифференцирующее звено.

 

6.3.3. Пропорционально-интегрально-дифференциальный (ПИД) закон регулирования

 

ПИД - закон регулирования - регулирующее воздействие пропорционально сумме рассогласования, интегралу и производной рассогласования.

где

Т_пр - время предварения (опережения);

Т_и - время изодрома;

К_р - коэффициент передачи.

Преобразуем уравнение по Лапласу:

.

Отсюда

.

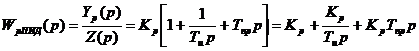АФХ ПИД - регулятора

,

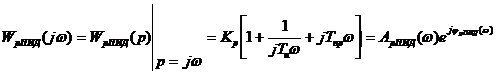где

График АФХ приведен на рисунке 6.5.

∞

K_p

ω

₀ u()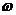

ω

∞

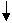
Рис.6.5.

Переходная функция регулятора

График переходной функции приведен на рисунке 6.6.

 

h_пид

 

К_р

t

⁰

Рис.6.6.

 

Если ПИД – регулятор реализуется с помощью обратной связи, охватывающей только усилитель, а исполнительный механизм является интегрирующим звеном,

то

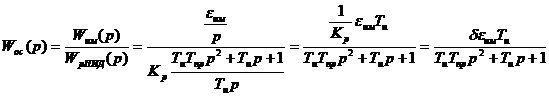
или

,

Здесь ; .

Следовательно, обратная связь должна быть выполнена в виде апериодического звена второго порядка или в виде последовательного соединения двух апериодических звеньев первого порядка. Такую обратную связь называют жесткой с инерционностью второго порядка.

Если обратная связь охватывает и усилитель и исполнительный механизм,

то

или

.

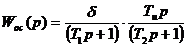Следовательно, обратная связь в этом случае должна быть выполнена в виде дифференцирующего звена второго порядка или в виде последовательного соединения апериодического звена первого порядка и реального дифференцирующего звена.

7. СТРУКТУРНЫЕ СХЕМЫИ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ АСР

 

7.1. Одноконтурная АСР

 

В общем случае простейшая одноконтурная АСР может быть представлена структурной схемой, приведенной на рисунке 7.1.

 

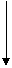
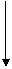f_втр(t) f_вн(t)

W_овн(p)

y_з(t) z(t) y_p(t) y(t)

+

W_p(p)

-

 

W_op(p)

 

Рис.7.1.

На рисунке обозначены:

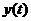- текущее значение регулируемой величины;

- заданное значение регулируемой величины;

- рассогласование (ошибка);

) - регулирующее воздействие;

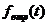- внутреннее возмущение;

- внешнее возмущение;

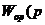) - передаточная функция объекта регулирования по каналам регулирующего воздействия и внутреннего возмущения;

- передаточная функция объекта регулирования по каналу внешнего

возмущения;

- передаточная функция регулятора;

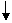- сумматор;

- сумматор с противоположными по знаку входными сигналами.

+

-

 

Когда к системе регулирования приложены управляющее воздействие, внутреннее и внешнее возмущения, то изображение регулируемой величины можно записать в виде:

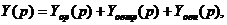
где , , 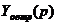- изображения отклонений регулируемой величины за счет

регулирующего воздействия, внутреннего и внешнего

возмущений соответственно.

 

Так как

то

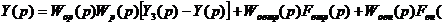
или

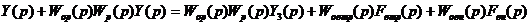
Отсюда

и

Следовательно, передаточная функция замкнутой одноконтурной АСР, связывающая любую выходную величину с любым входным воздействием , приложенным к произвольной точке системы, выражается в виде:

,

где

- передаточная функция элементов разомкнутой системы,

расположенных между точкой приложения возмущающего воздействия и точкой снятия выходного сигнала;

- передаточная функция всей разомкнутой системы.

При анализах АСР может представлять интерес поведение рассогласования 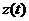при приложении к системе соответствующих возмущений.

В соответствии с вышеизложенным передаточные функции в этом случае принимают вид:

.

 

7.2. Многоконтурная АСР

 

К схеме, изображенной на рисунке 7.1, может быть приведена любая многоконтурная АСР, содержащая произвольное число соединенных друг с другом контуров и имеющая перекрестные связи.

Так как всякая структурная схема представляет собой линейную систему в виде некоторых более простых систем, точек разветвления сигналов (узлов) и сумматоров, соединенных между собой различными способами, то любое преобразование в структурной схеме сводится к попарной перестановке ее соседних элементов. Основной принцип перестановки элементов структурной схемы – все входные и выходные сигналы преобразуемого участка системы должны оставаться неизменными.

Из общего принципа вытекают конкретные правила структурного преобразования, использовав которые, можно свести любую многоконтурную систему к типовым соединениям звеньев. Заменив затем эти типовые соединения эквивалентными звеньями, многоконтурную систему приводят к одноконтурной.

Некоторые примеры правил структурных преобразований приведены в

таблице 7.1.

 

Таблица.7.1.

 

Операция	Исходная схема	Эквивалентная схема
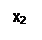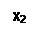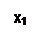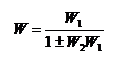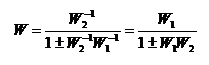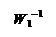
Замена звеньев прямой и обратной цепей.     Переход к единичной обратной связи	x1 x2	x1 x2

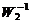
8. АСТАТИЗМ АСР