ЛИНЕЙНЫЕ НЕПРЕРЫВНЫЕ АСР 10 глава

Поэтому в качестве приближения целесообразно выбрать такой метод, который гарантировал бы наилучшее приближение в окрестности точки с нулевой частотой. Поставленному требованию достаточно хорошо удовлетворяет метод приближения путем разложения функции в ряд Тейлора.

Отклонение частотной характеристики от нуля тем меньше, чем больше членов ряда обращаются в нули.

Отсюда, условия оптимальности запишутся в виде:

 

 

Исходя из этих условий, для различных законов регулирования получены условия оптимальности, приведенные в таблице 12.1.

 

 

Таблица12.1.

Закон Регулирования	Параметры настройки	Условие оптимальности
П     И     ПИ     ПИД		, , , ,

 

 

12.1.2. Графо - аналитический расчет настроек АСР по показателю колебательности

 

12.1.2.1. Условие обеспечения заданного значения показателя колебательности

 

В качестве меры устойчивости системы используют максимум амплитудно - частотной характеристики системы по каналу управляющего воздействия, т.е. показатель колебательности (М). Чем больше максимум АЧХЗС, тем ближе АФХРС к критической точке (-1; 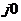) комплексной плоскости и, следовательно, тем меньше запас устойчивости имеет система.

Чтобы система имела некоторый заданный запас устойчивости, т.е. чтобы максимум АЧХЗС не превышал некоторого значения М_зад, необходимо, чтобы АФХРС не заходила во внутрь области, ограниченной окружностью радиуса

с центром на отрицательной вещественной полуоси на расстоянии

от начала координат (рис. 12.1 а)

jV(ω) jV(ω)

r_зад r_зад

M_зад M<M_зад M_зад M=M_зад

⁰ u(ω) ⁰ u(ω)

R₀ R₀

W_pc(jω)

а) б)

Рис.12.1.

 

При равенстве показателя колебательности его заданному значению АФХРС должна касаться этой окружности (рис. 12.1.б).

Проведем прямую ОА, касающуюся окружности заданного индекса М_зад

(рис. 12.2).

Из рисунка 12.2 имеет:

Подставляя сюда значения и , получим:

jV(ω)

R₀

M_зад r_з

0₁ ^{ß 0} u(ω)

A

 

 

Рис.12.2.

 

Это означает, что независимо от масштаба графика окружность с индексом М_зад всегда остается касательной к прямой ОА, проведенной из начала координат под углом к отрицательной вещественной полуоси. Следовательно, при величине коэффициента передачи регулятора, соответствующей заданному запасу устойчивости системы, окружность с индексом М_зад должна касаться одновременно АФХРС (рис. 12.1 б) и прямой, проведенной под углом к отрицательной вещественной полуоси из начала координат комплексной плоскости (рис. 12.2).

Введя АФХРС при единичном коэффициенте передачи регулятора, несложными геометрическими построениями можно показать, что:

,

где - радиус окружности, касающейся одновременно АФХРС и прямой, проведенной под углом

к отрицательной вещественной полуоси из начала координат комплексной плоскости.

Отсюда вытекает следующий порядок расчета оптимальных настроек регуляторов.

 

 

12.1.2.2. АСР с П - регулятором

 

1. Вычерчивают АФХРС при К_р=1 (единичном коэффициенте передачи), т.е. (рис.12.3)

 

jV(ω)

M_зад r

0₁ ^{ß 0} u(ω)

A

W_pc(jω)

 

Рис.12.3.

 

2. Из начала координат проводят прямую под углом

к отрицательной вещественной полуоси.

3. Чертят окружность с центром на вещественной отрицательной полуоси, касающуюся одновременно АФХ объекта регулирования и этой прямой.

4. По замеренному значению радиуса окружности находят значение оптимального коэффициента передачи

 

 

12.1.2.3. АСР с И - регулятором

 

 

1. Для удобства графических построений АФХ И - регулятора представляют в виде:

где

- условный коэффициент передачи И - регулятора;

- условная постоянная времени И - регулятора

2. По АФХ объекта (статического) строят АФХРС при =1 и некотором значении постоянной , величину которой можно выбирать любой, удобной для построения характеристики.

 

Для построения этой характеристики нужно каждый вектор , предварительно разделенный по модулю на w,повернуть на 90º по часовой стрелке (рис. 12 4).

jV(ω)

 

 

А_об(ω_i) ₀ φ_об(ω_i) u(ω)

T_pω_i 90⁰

A_об(ω_i)

ω_i

ω_i

 

Рис.12.4.

 

2. Проводят прямую под углом

к отрицательной вещественной полуоси и чертят окружность с центром на этой полуоси, касающуюся одновременно этой прямой и характеристики . Величина , обеспечивающая необходимую величину М_зад, определяется как:

Следовательно,

 

 

12.1.2.4. АСР с ПИ - регулятором

 

Разомкнутая АСР с ПИ - регулятором описывается передаточной функцией

При К_р=1

Отсюда

Это означает, что включение ПИ - регулятора приводит к добавлению к векторам этих же векторов, повернутых на 90º по часовой стрелке и измененных по модулю в раз (рис. 12.5.a.).

jV(ω) jV(ω)

k_p=1

φ_об(ω_i) r₃ r₂

u(ω) o₃ o_{2 0} u(ω)

⁰ φ_рс(ω_i) ß

90⁰ A_об(ω_i)

A_pc(ω_i) T_и=а

∆A(ω_i) T_и=с T_и=b

α

ω_i

a) б)

Рис.12.5.

 

Отсюда следует, что АФХРС при К_р=1 может быть построена графически при наличии графика или рассчитана аналитически.

Из рисунка 12.5 а имеем:

откуда

 

Здесь берется по абсолютному значению. Далее расчет настроек производят в порядке:

1. Тем или иным способом строят семейство АФХРС при К_р=1 и некотором

фиксированном значении времени изодрома Т_и, (т.е. временем изодрома Т_и

задаются).

2. Проводят прямую из начала координат под углом к отрицательной вещественной полуоси и строят окружности, касающиеся одновременно этой прямой и характеристик для различных значений Т_и (рис.12.5 б).

3. Вычисляют оптимальные значения коэффициента передачи регулятора по

найденным значениям радиусов соответствующих окружностей

 

4. По результатам расчета в плоскости параметров К_р-Т_и строят границу заданного

показателя колебательности (рис. 12.6)

k_p

М<M_зад М=M_зад

к_{р опт}

М>M_зад

 

₀ Т_{и опт} T_и

 

 

Рис.12.6.

 

Оптимальной настройке будет соответствовать точка в той области, для которой . Этому условию удовлетворяет точка касания касательной, проведенной из начала координат к границе заданного показателя колебательности (к границе устойчивости, заданной показателем колебательности М).

 

12.1.2.5 АСР с ПИД - регулятором

 

Для определения оптимальных настроек ПИД - регулятора строится семейство АФХРС для единичного коэффициента передачи регулятора и различных значений времени изодрома при фиксированном оптимальном значении отношения времени предварения ко времени изодрома

Передаточная функция разомкнутой системы с ПИД - регулятором имеет вид:

При К_р=1

,

,

Подставив , получим:

Следовательно, включение ПИД - регулятора приводит к добавлению к векторам этих же векторов, повернутых на 90º по часовой стрелке и измененных по модулю в раз (рис. 12.7)

jV(ω)

 

φ_об(ω_i)

u(ω)

⁰ φ_рс(ω_i)

ω_i 90⁰ A_об(ω_i)

A_pc1(ω_i)

ω_i

α

ω_i

 

Рис.12.7.

 

В соответствии с рисунком 12.7

,

,

.

Подставив значение ,находим:

 

Далее расчет настроек ПИД регулятора аналогичен расчету настроек ПИ - регулятора.

 

 

12.1.2.6. Расчет приближенных настроек П и ПИ - регуляторов с помощью АФХОР

 

Из рассмотренной методики расчета оптимальных настроек АСР вытекает, что основное значение для расчета имеет участок АФХОР, расположенный вблизи ее пересечения с отрицательной вещественной полуосью комплексной плоскости.

Это обстоятельство позволяет осуществить приближенную настройку регулятора, предполагая, что в окрестности частоты, соответствующей точке пересечения характеристики с отрицательной вещественной полуосью, АФХОР мало отличается от характеристики интегрирующего звена с запаздыванием.

На этом основании для случая М=1,62 (что соответствует y=0,75) получены упрощенные расчетные соотношения для П и ПИ - регуляторов, приведенные в таблице 12.2.

Таблица 12.2

Приближенная настройка
П – регулятора	ПИ – регулятора
Кропт	Кропт	Тиопт
Для астатических объектов
Для астатических и статических объектов

 

В таблице 12.2 обозначены:

- частота, при которой , т.е. частота, при которой пересекает отрицательную вещественную полуось комплексной плоскости;

- модуль вектора , фаза которого , т.е. модуль вектора , соответствующего точке пересечения с отрицательной вещественной полуосью;