ЛИНЕЙНЫЕ НЕПРЕРЫВНЫЕ АСР 12 глава

ω_k

₀ u(ω)

α_k

A

 

Рис.12.15.

 

Частный случай передаточной функции, когда комплексная переменная ,

называют расширенной частотной функцией. Она может быть получена как отношение вынужденного движения на выходе из системы ко входному затухающему синусоидальному воздействию

При изменении получим расширенную АФХ.

В случаях ограничения с использованием критерия Найквиста находилась область устойчивого регулирования в плоскости параметров регулятора.

При ограничении совокупность настроечных параметров регулятора, соответствующая контуру АОВ (рис.12.15) в комплексной плоскости корней, образует внутри области устойчивости в плоскости параметров К_р-Т_и линию равного затухания (т.е. линию заданной степени колебательной устойчивости).

Таким образом, расчет АСР на заданную степень затухания можно произвести, используя расширенную АФХ.

Расширенную АФХ записывают в виде:

,

где - расширенные вещественная, мнимая, амплитудная и фазовая частотные характеристики.

 

 

12.1.4.2. Расчетные соотношения

 

По аналогии с условием границы устойчивости можно записать условие границы запаса устойчивости в виде:

,

где - расширенная АФХ разомкнутой АСР.

Это равенство означает наличие затухающих колебаний с определенной степенью затухания .

 

 

Расширенная АФХРС может быть представлена в виде произведений соответствующих характеристик регулятора и объекта

Отсюда

или

и

где

- расширенные АЧХ регулятора и объекта;

- расширенные ФЧХ регулятора и объекта;

- обратная расширенная АЧХ объекта;

берется здесь по абсолютному значению.

Решением системы уравнений относительно настроечных параметров

; ; (где )

получены расчетные уравнения для определения настроек различных регуляторов.

Например, для ПИ - регуляторов

или

Здесь и - обратные расширенные вещественная и мнимая частотные характеристики объекта регулирования.

Расчетные соотношения можно выразить и через обычные расширенные АФХ.

Подставив

и

)

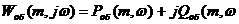в уравнение границы заданного запаса устойчивости (через m)

,

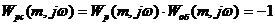получим расчетное уравнение в виде

 

Например, для ПИ – регулятора с передаточной функцией

подстановкой получим

Отсюда

где

 

12.1.4.3. Порядок расчета

 

Из приведенных расчетных соотношений вытекает следующий порядок расчета настроек АСР:

 

1. Из передаточной функции подстановкой получают расширенные частотные характеристики объекта: , , ,

, , , .

2. Подставляя в эти уравнения численные значения параметров объекта и выбранную величину m, получают

; .

3. В последние уравнения подставляют численные значения частоты от нуля до значения, при которым С₀ становится отрицательной величиной.

4. Строят в координатах С₀-С₁ линию равной степени затухания в виде совмещенного графика зависимостей и .Все значения пар С₀,С₁, соответствующие отдельным точкам линии равной степени затухания (рис. 12.16), обеспечивают заданную степень затухания (заданную величину m)

С₀

ω₁

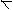
ω₂ Ψ_зад=const

ω₀

ω₃ Ψ<Ψ_зад

ω5

ω₄

 

₀ С₁

 

Рис.12.16.

5. Выбор оптимальных значений С₀ и С₁.

Из рисунка 12.16 видно, что одну и ту же степень затухания можно получить при различном сочетании параметров настройки регулятора.

 

Однако, другие показатели качества регулирования (максимальное динамическое отклонение, степень перерегулирования, длительность переходного процесса) при этом будут различными. На основе многочисленных расчетов переходных процессов для различных пар С₀,С₁ и экспериментальным путем установлено, что оптимальному процессу соответствует точка на кривой , лежащая "немного" правее и ниже максимума этой кривой.

Для более определенного выбора точки на кривой , соответствующей оптимальной настройке регулятора, следует на этом же графике линии построить кривую квадратичной интегральной оценки

Для этого значение интеграла следует представить в виде конечной суммы через амплитудно-частотный спектр переходного процесса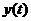

,

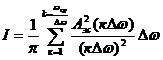где

- АЧХ замкнутой АСР по каналу рассматриваемого возмущения относительно регулируемой величины;

- частота среза.

При этом значения интегрального критерия достаточно рассчитать для тех нескольких пар параметров, которые расположены на максимуме и справа от максимума кривой . Минимум этого интеграла и определит точку на кривой , соответствующую оптимальной паре настроек С₀ и С₁ (рис. 12.17).

 

C₀

 

Ψ_зад=const

I

C_опт

 

I_мин

C₁

Рис.12.17.

 

12.2. Переходные процессы (процессы регулирования) в замкнутой АСР

 

12.2.1. Введение

 

Последним этапом определения оптимальных настроек регуляторов является расчет переходных процессов в замкнутой АСР. По показателям качества переходного процесса и судят о оптимальности найденных настроечных параметров регуляторов.

Для расчета переходных процессов можно применять различные методы: решение дифференциального уравнения замкнутой системы; обратное преобразование Лапласа с использованием теорем разложения Хевисайда; метод z-форм, основанный на дискретном преобразовании Лапласа; метод переменных состояния; метод, основанный на использовании частотных характеристик.

В последнем случае наиболее употребительным является метод Акульшина, основанный на использовании вещественных и мнимых или амплитудных и фазовых частотных характеристик.

 

12.2.2. Расчет переходного процесса по вещественной и мнимой или амплитудной и фазовой частотным характеристикам

 

Расчет основан на представлении процесса регулирования как реакции системы на периодическую последовательность прямоугольных импульсов, причем колебания мыслятся такими, что переходный процесс заканчивается в течение полупериода. В этом случае в течение каждого полупериода переходный процесс будет совпадать с реакцией системы на ступенчатое воздействие.

Входное воздействие в виде последовательности прямоугольных импульсов (в виде последовательности скачкообразной функции) и соответствующую ей реакцию системы можно представить суммами нечетных гармоник разложения функций воздействия и реакции в соответствующие ряды Фурье. В связи с этим выражение для определения изменения регулируемой величины 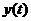при скачкообразном входном воздействии 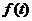высотою принимает вид:

или

,

где

-вещественная, мнимая, амплитудная, фазовая частотные характеристики замкнутой системы;

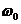-частота основной гармоники разложения функций в ряд Фурье;

-номер нечетной гармоники;

m -номер старшей гармоники разложения;

-время регулирования (время переходного процесса);

-шаг по оси времени при построении кривой переходного процесса;

-символ, обозначающий последовательность ординат переходного процесса в шаговые моменты времени;

-символ суммирования.

 

Частоту 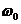разложения выбирают так, чтобы значение амплитуды при не превышало (5¸10)% резонансной амплитуды (рис. 12.18), т.е. из условия

 

 

А_зс

 

 

 

 

А_зс(ω_рез)

 

А_зс(0)

₀ ω_рез ω

 

Рис.12.18.

 

При расчете можно ограничиться значениями m в пределах (11¸17).

Частоту 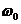можно также принимать равной 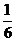рабочей частоты, при этом под рабочей частотой понимают частоту, которая соответствует выбранным оптимальным настройкам регулирующего устройства.

Продолжительность переходного процесса можно оценить по резонансной частоте, как

Расчет следует выполнять с таким шагом , чтобы за время регулирования получилось (20¸30) ординат кривой переходного процесса.

13. Расчет настроек линейных непрерывных двухконтурных АСР

 

13.1 Введение

 

Определение оптимальных настроек двухконтурных АСР сложнее по сравнению с одноконтурной. Надежное решение задачи возможно только при использовании моделирующих устройств. При этом область приближенных параметров настройки, в которой следует искать точное значение их, находят предварительным расчетом.

Методика таких расчетов базируется на предположении о возможном расчете какого либо контура независимо от другого. Могут быть и случаи, когда расчет двухконтурных систем путем выделения одного контура и расчета его настройки независимо от другого практически определяет параметры, близкие к оптимальным.

Часто встречаются два таких случая:

 

1. В процессе работы АСР один из регуляторов может быть отключен и в работе участвует только один регулятор.

 

2. Инерционность одного контура значительно меньше инерционности другого. В этом случае переходные процессы в малоинерционных контурах успевают практически стабилизироваться до того, как они возникнут во втором контуре.

 

 

13.2. Двухконтурная АСР с корректирующим и стабилизирующим регуляторами.

 

Примером такой АСР может быть система регулирования давления пара в паровой магистрали за котлом, поддерживающая давление в этой магистрали путем воздействия на задатчик регулятора тепловыделения в топке котла (рис. 13.1)

Р_пара

пар

(y(t))

 

 

 

Q

(y₁(t))

 

у_р(t)

топливо

Рис.13.1.

На рисунке 13.1:

РД – регулятор давления, воспринимающий сигнал по давлению пара R_пара за котлом,

РТ – регулятор тепловыделения (регулятор топлива), воспринимающий сигналы от регулятора давления и по тепловыделению в топке котла.

Регулятор давления является корректирующим регулятором, воспринимающим сигнал по давлению пара и восстанавливающим его до прежнего номинального (рабочего) значения при новой нагрузке котла. Эта схема является простейшей разновидностью каскадных систем регулирования.

Для такой АСР можно рекомендовать следующую методику расчета настроечных параметров.

 

Случай 1.

 

1. По передаточной функции , которая связывает промежуточную регулируемую величину с регулирующим воздействием (рис. 13.2), находится оптимальная настройка стабилизирующего регулятора в предположении, что корректирующий регулятор отключен.

Wоб

P_k Р_ст

Wрк

y_з(t) y_зк(t) у_рст y(t)

Wрcт

(p_зад) (Q_зад) (p)

- - W_об1

y(t) y₁(t)

(p) (Q)

Рис.13.2.

 

2. Определяется оптимальная настройка корректирующего регулятора. Для него регулируемым объектом является система, состоящая из объекта и контура стабилизирующего регулятора. Поэтому при расчете настроек корректирующего регулятора нужно исходить из передаточной функции эквивалентного объекта.

).

Случай 2.

 

1. Если инерционность объекта относительно промежуточной регулируемой величины значительно меньше инерционности относительно основной регулируемой величины 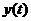, то быстродействие регулятора может быть сделано значительно большим быстродействия регулятора . В связи с этим, изменение заданного значения регулятору происходит настолько медленно, что практически этот регулятор успевает поддержать величину почти точно на заданном значении, т.е. в процессе работы = .

Тогда

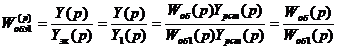
2. После определения настройки корректирующего регулятора находится оптимальная настройка стабилизирующего регулятора по передаточной функции