СИСТЕМА НАТУРАЛЬНЫХ ЧИСЕЛ

 

Аксиомы Пеано. Пусть N – некоторое множество, на котором определено бинарное отношение следования S(n). Система 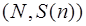называется натуральным рядом, если удовлетворяет следующим аксиомам:

1. 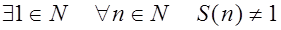, т.е. в N существует элемент 1, называемый единицей, который непосредственно не следует ни за каким натуральным числом.

2. 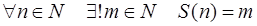, т.е. за каждым натуральным числом непосредственно следует, и при том только одно, натуральное число.

3. 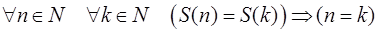, т.е. каждое натуральное число непосредственно следует не более чем за одним натуральным числом.

4. Аксиома индукции:

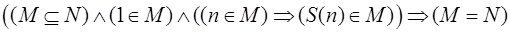, т. е. если некоторое подмножество М множества N содержит 1 и вместе с каждым своим элементом содержит непосредственно следующий за ним, то такое подмножество совпадает с множеством N.

Теорема. Аксиомы Пеано независимы, т.е. ни одна из них не вытекает из других.

Теорема. Аксиоматическая теория натуральных чисел – непротиворечива, т.е. в этой теории невозможно существование одновременно некоторого высказывания А и его отрицания .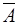

Теорема (принцип полной математической индукции). Предложение T(n) истинно для всех n натурального ряда, если выполнены следующие условия:

1) Т(1) – истинно;

2) каково бы ни было натуральное число k, из предположения о том, что T(k) – истинно, следует, что T(S(k)) – также истинно.

Пример 1. Докажите, что сумма первых n нечетных натуральных чисел равно n².

Доказательство.

В нашем случае нужно доказать, что для всех натуральных n истинно равенство 1+3+5+…+(2n-1) = n².

1. Проверим для n=1: 1=1². Очевидно, это равенство верно.

2. Пусть 1+3+5+…+(2n-1)=n² – верно. Докажем, что 1+3+5+…+(2n+1) = (n+1)² –также верно

Действительно, 1+3+5+…+(2n-1)+(2n+1) 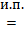n²+(2n+1) = (n+1)².

Приведенный в доказательстве текст составляет «бланк доказательства». Если убрать все остальное, то «бланк» готов для нового заполнения – доказательства нового утверждения. В пункте 1 запись T(1) получается из предложения T(n) заменой всюду n на 1. В пункте 2 запись понимается как «пусть T(n) – истинно для фиксированного n, докажем, что T(n+1) – истинно». При этом T(n+1) получается из T(n) заменой n на n+1. Момент использования индуктивного предположения здесь выделено пометкой «и. п.». Преобразования после использования индуктивного предположения должны быть направлены на получение заранее сформулированного результата. Такая стандартизация доказательства по индукции позволяет выполнять его почти автоматически. Единственный момент, требующий размышлений, – это доказательство истинности предложения T(S(k)).

Пример 2. Ханойская башня

Есть три штырька, на который можно насаживать n дисков разного размера. В начальный момент времени все диски насажены на одном штырьке в порядке убывания размера. За один ход разрешается переносить верхний в стопке диск на любой другой штырек так, чтобы под ним был диск большего размера. Требуется перенести всю стопку дисков с одного штырька на другой. Утверждается, что это возможно при любом n.

Доказательство. База очевидна (один диск можно переносить на любой штырек). Индуктивный переход: воспользовавшись предположением индукции, перенесем верхние n–1 диск на второй штырек. Потом нижний – самый большой – на третий. И, еще раз воспользовавшись предположением индукции, перенесем стопку из n–1 диска на третий штырек.

Пример 3. Принцип Дирихле

При решении задач «на доказательство» часто бывает полезен так называемый «принцип Дирихле». В самой простой форме он звучит так: «нельзя посадить трёх кроликов в две клетки так, чтобы в каждой клетке находилось не больше одного кролика». Или, «если в N клетках сидит не меньше чем N+1 кроликов, то найдётся клетка, в которой сидит не меньше двух кроликов».

Принцип Дирихле несложно доказывается методом полной математической индукции.

Оказывается, что это простое утверждение помогает в решении самых разных задач. Главное – понять, что в задаче клетки, а что кролики. Иногда используют обобщённый принцип Дирихле: «Пусть в N клетках сидит не менее kN+1 кроликов, тогда в какой-то из клеток сидит не менее k+1 кроликов».

Сложение на множестве натуральных чисел. Определение. Сложением натуральных чисел называется бинарная операция «+», удовлетворяющая аксиомам:

1) ;

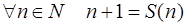2) .

Теорема. Сложение натуральных чисел существует и единственно.

Пример. Обозначим S(1)=2, S(2)=3, S(3)=4, S(4)=5.

Найдем 3+2: 3+2=3+S(1)=S(3+1)=S(S(3))=S(4)=5.

Найдем 2+3: 2+3=2+S(2)=S(2+2)=S(2+S(1))=S(S(2+1))=S(S(S(2)))= =S(S(3))=S(4)=5.

Свойства сложения

1. Сложение натуральных чисел – ассоциативно.

Докажем (p+m) +n = p+(m+n) индукцией по n:

1) для n =1: (p+m) +1 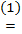S(p+m) 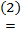p+S(m) 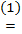p+(m+1) – верно;

2) если (p+m) +k = p+(m+k) – верно, докажем для n=k+1:

(p+m)+(k+1)=(p+m)+S(k)=S((p+m)+k)=S(p+(m+k))=p+S(m+k)=

=p+(m+S(k))=p+(m+(k+1)).

2. Сложение натуральных чисел – коммутативно.

Будем доказывать n+m=m+n индукцией по m. Для этого сначала проверим, что n+1=1+n. Докажем n+1=1+n индукцией по n:

1) при n = 1: 1+1 = 1+1 – очевидно;

2) из k+1=1+k следует S(k)+1=S(S(k))=S(k+1)=S(1+k)= =1+S(k).

Докажем теперь n+m = m+n индукцией по m:

1) для m=1: n+1=1+n – доказано выше;

2) из n+k=k+n следует n+S(k)=S(n+k)=S(k+n)=k+S(n)= =k+(n+1)=k+(1+n)=(k+1)+n=S(k)+n.

3. Сложение обладает свойством сократимости, т.е. из p+n=m+n следует p=m.

Докажем индукцией по n:

1) при n=1: из p+1=m+1 следует S(p)=S(m), тогда, согласно аксиомам Пеано, p=m;

2) если из p+k=m+k следует p=m, то тогда из p+S(k)=m+S(k) получим S(p+k)=S(m+k), откуда(по 2 аксиоме Пеано) имеем: p+k = m+k, следовательно, по предположению индукции, p=m.

Умножение натуральных чисел. Определение. Умножением натуральных чисел называется бинарная операция «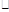 », определенная на множестве N, которая удовлетворяет аксиомам:

1. ;

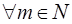
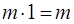2. .

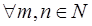
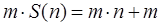Замечание. На множестве натуральных чисел определена вторая операция. Для удобства записи традиционно используем приоритет операций и, соответственно, соглашение о скобках. Это уже учтено при записи второй аксиомы умножения.

Теорема. Умножение натуральных чисел существует и единственно.

Свойства

1. Умножение натуральных чисел дистрибутивно относительно сложения: 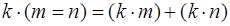и для любых натуральных k, m, n.

2. Умножение натуральных чисел ассоциативно, т.е. 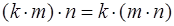для любых натуральных k, m, n.

3. Умножение натуральных чисел коммутативно, т.е. 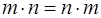для любых натуральных m, n.

Пример. В школе произведение 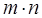трактуется как сума n слагаемых, каждое из которых равно m:

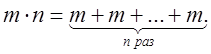
Согласно введенному аксиоматическому определению так и получается. Найдем согласно данному выше аксиоматическому определению, например, 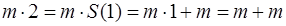. Или, например, . В результате в каждом примере получили привычное «школьное» умножение натуральных чисел.

Для введения бинарного отношения «меньше» на множестве натуральных чисел и доказательства его свойств перечислим необходимые вспомогательные предложения.

Предложение 1. Всякое натуральное число 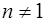непосредственно следует за некоторым натуральным числом.

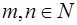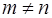Предложение 2. Для любых если , то .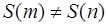

Предложение 3. Для любых натуральных m, n выполняется неравенство .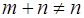

Следствие. Для любого натурального n выполняется неравенство .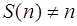

Теорема 1. Для любых натуральных чисел a и b имеет место одно, и только одно, из соотношений:

1) существует натуральное k такое, что b=а+k;

2) а=b;

3) существует натуральное m такое, что a=b+m.

Отношение «меньше» для натуральных чисел. Определение. Будем говорить, что натуральное число а меньше натурального числа b, и писать а<b, если существует натуральное число k такое, что b=a+k.

В математике активно эксплуатируется представление о том, что натуральные числа можно «выстроить в линейку», используя отношение <. При этом используется то, что про любые два натуральных числа а и b можно однозначно сказать: либо а<b, либо а=b, либо b<а. Это свойство называется свойством трихотомии, что в переводе означает «одно из трех». Важным свойством отношения «меньше» является также возможность сравнить числа а и с «транзитом» через «посредника» b: если а<b и b<с, то а<с. Это так называемое свойство транзитивности. Уточним эти представления в виде строгих определений.

Определение. Система 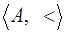с основным множеством А и бинарным отношением < (меньше) называется линейно упорядоченным множеством, если выполнены следующие два условия:

1) (свойство трихотомии). Для любых 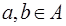имеет место одно и только одно из соотношений: ;

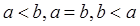2) (свойство транзитивности). Для любых 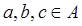если 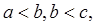то а < с.

При этом отношение < называется отношением линейного порядка.

Теорема. Система 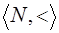является линейно упорядоченным множеством.

Введем отношения Определение. Пусть дано линейно упорядоченное множество 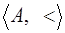. Для любых 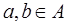положим:

1) а>b (а больше b) тогда и только тогда, когда b<а;

2) 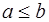(а меньше или равно b) тогда и только тогда, когда а<b или a=b;

3) 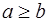(а больше или равно b) тогда и только тогда, когда а>b или a=b.

Предложение. Отношение 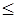обладает следующими свойствами:

1) рефлексивности: ;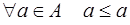

2) антисимметричности: ;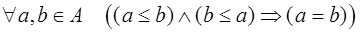

3) транзитивности: ;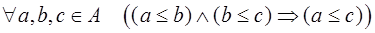

4) линейности: .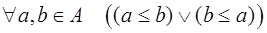

Предложение. Единица 1 – наименьший элемент во множестве N.

Предложение (свойство дискретности). Для любого 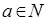не существует такого, что 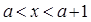, т. е. между а и a+1=S(a) нет ни одного натурального числа.

Следствие. Для любых 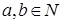если a<S(b), то 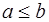и, если a<b, то .

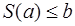Различные виды доказательств по индукции. Приведем принцип полной математической индукции, в котором делается более сильное индуктивное предположение.

Теорема (усиленный принцип полной математической индукции) Предложение Т(n), зависящее от натуральной переменной n, верно для любого натурального числа, если выполнены следующие условия:

1) Т(n) верно для n = 1, т.e. Т(1) истинно;

2) каково бы ни было натуральное число m, из предположения о том, что Т(n) истинно для всех n < m, следует, что оно верно и для m, т.е. Т(m) истинно.

Иногда истинность утверждения Т(n) нужно доказать для всех натуральных чисел, начиная с некоторого натурального числа а, причем а не обязательно совпадает с 1. Тогда используется следующая теорема.

Теорема (обобщенный принцип полной математической индукции)

Предложение Т(n) верно для любого натурального числа 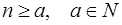, если выполнены следующие условия:

1) предложение Т(n) верно для n=a, т.e. Т(а) – истинно;

2) каково бы ни было натуральное число 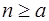, из предположения о том, что Т(n) – истинно, следует, что Т(S(n)) –также истинно.

Приведем, наконец, принцип полной математической индукции, который соединяет в себе черты усиленного и обобщенного принципов.

Теорема. Предложение Т(n) верно для любого натурального числа 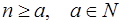, если выполнены следующие условия:

1) предложение Т(n) верно для n=a, т.е. Т(а) – истинно;

2) каково бы ни было натуральное число 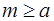, из предположения о том, что Т(n) – истинно для всех натуральных n таких, что , следует истинность Т(m).

Предложение. Сложение и умножение натуральных чисел – монотонны, т. е.

.

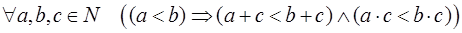Определение. Система (К, +, •, <) с основным множеством К, бинарными операциями сложения + и умножения • и бинарным отношением < называется упорядоченным полукольцом, если выполнены следующие условия:

1) (К, +,•) – полукольцо, содержащее более одного элемента;

2) (К, <) – линейно упорядоченное множество;

3) операции сложения и умножения монотонны: 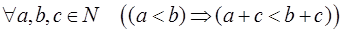(монотонность сложения), 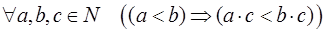(монотонность умножения).

Очевидно, система (N, +, •, <) является упорядоченным полукольцом.

Определение. Система (N, +, •, <) называется упорядоченным полукольцом натуральных чисел.

Определение. Пусть дано полукольцо (К, +, •). Напомним, что если существует элемент 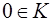, такой что для любого 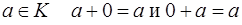, то этот элемент называется нулем полукольца К. Если существует элемент 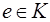, такой что для любого 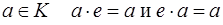, то этот элемент называется единицей полукольца К.

Очевидно, полукольцо натуральных чисел не содержит нуля, но содержит единицу. Заметим также, что если упорядоченное полукольцо содержит ноль 0, то условие c<с+с эквивалентно условию с>0.

Предложение. В упорядоченном полукольце натуральных чисел при почленном сложении или перемножении верных неравенств одинакового смысла получим снова верные неравенства.

Предложение. Сложение и умножение натуральных чисел обладают свойствами сократимости, т.е.

,

.

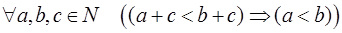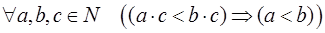Для сложения свойство сократимости было доказано выше, для умножения свойство сократимости предоставляем доказать самостоятельно.

Предложение. В упорядоченном полукольце натуральных чисел выполняется аксиома Архимеда:

.
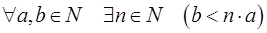