Сценарий
Практической работы № 2 по дисциплине «Теоретические основы электротехники» по направлению 13.03.02 Электроэнергетика и электротехника.
Группа ЭЭ-16-Д(3-й семестр)
Способы изображения синусоидальных функций времени
Введение (5-10мин.)
Цель работы: Отработать навыкипреобразования синусоидальных функций для представления в различных формах.
Общие теоретические сведения
Синусоидальные функции времени могут быть представлены тригонометрической формой записи, линейными диаграммами изменения синусоидальной величины во времени, вращающимися векторами и комплексными числами.
Тригонометрическая форма записи синусоидально изменяющейся во времени величины в общем виде представляется выражением
a = Am sin (ωt + + ψ) = Am sin α,
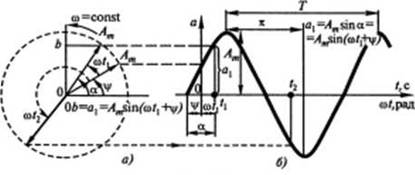
где α - мгновенное значение синусоидальной функции времени; Am - амплитудное значение синусоидальной функции времени; ω -угловая или круговая частота, характеризующая скорость изменения фазового утла; t - текущее значение времени; α = (ω t + ψ) - фаза или фазовый угол (аргумент синусоидальной функции времени); ψ - начальная фаза (начальный фазовый угол) (рисунок 1, а).
В соответствии с выражением для мгновенного значения сину-соидальная функция времени во многих случаях изображается в ви-де линейной диаграммы - графика изменения соответствующей си-нусоидальной функции от времени (от угла ω).(рисунок 1, б).
 |
Период изменяющейся во времени синусоидальной величины Т = 1/f (f - частота синусоидально изменяющейся во времени величины (число периодов в секунду)]. В электротехнике кроме мгновенных используются действующие и средние значения.
Рисунок 1– Способы представления синусоидального тока: а) круговая диаграмма; б) временная диаграмма (эпюра напряжений).
Действующие значения синусоидально изменяющейся ЭДС напряжений и токов записывают соответственно в виде выражений:
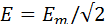=0,707 
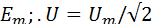=0,707 
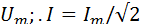=0,707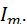 
Соответственно, средние значения синусоидально изменяющихся ЭДС, напряжений и токов:
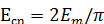=0,637 
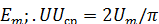=0,637 
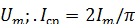=0,637 
Синусоидальная функция времени изображается также вращающимся вектором (см. рисунок 1, а). Длина вращающегося радиуса- вектора равна амплитуде Аm синусоидальной функции времени, угол между вращающимся вектором и осью абсцисс для момента времени t = 0 представляет начальную фазу у синусоидальной величины. Проекция вращающегося радиуса-вектора на ось ординат определяет мгновенное значение синусоидальной величины.
В электротехнике за положительное направление вращения векторов принято направление против хода часовых стрелок.
Синусоидальные функции времени a = Am sin (ωt + ψ) изображаются также комплексными числами. При этом на плоскости комплексных чисел (рисунок 2) из начала координат под углом у к оси действительных чисел (вещественной оси) проводят вектор Am, концу которого соответствует определенное комплексное число. Комплексная амплитуда синусоидальных величин определяется выражением 
(где е - основание натурального логарифма). Для действующих значений синусоидальных величин это выражение преобразуется к виду: 
.
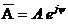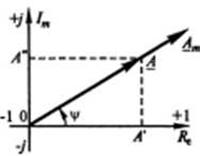
Рисунок 2– Векторное представление комплексного числа
С увеличением времени фаза α = (ωt + ψ) синусоидальной величины возрастает, при этом угол между радиусом-вектором и осью действительных величин увеличивается, радиус-вектор поворачивается на соответствующий угол против хода часовых стрелок. Для момента времени t1 (см. рисунок 1, б) комплексная амплитуда
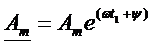
а действующее значение
Комплексное число представляет собой сумму действительной и мнимой частей:
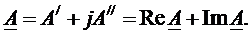
где А' - вещественная (действительная) часть комплексного числа; jA// - мнимая часть комплексного числа; Re и Im - символы, обозначающие дей-ствительную и мнимую части комплексного числа (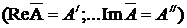
.
Комплексные числа А' ± jA// и А' ± jA//1 считаются равными, если их действительные и мнимые части равны (А' = А/1; ±jAm = ±jA”).
В выражении комплексного числа фигурирует также символ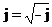 
- мнимая единица, с помощью которого из комплексного числа выделяется его мнимая составляющая. Умножение вектора А на множитель j соответствует повороту его на угол, равный π/2 в положительном направлении (против хода часовой стрелки), а умножение на j - повороту в отрицательном направлении (по ходу часовой стрелки).
Модуль комплексного числа: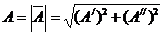 
, а его аргумент
ψ = arctg A// / A /.
Используют три формы записи комплексных чисел.
1. Алгебраическая (координатная) форма записи комплексного числа:
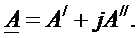
Сопряженное ему комплексное число имеет противоположный знак при мнимой части:
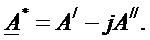
При этом произведение сопряженных комплексных чисел А А* = А2 оказывается равным квадрату модуля комплексного числа. При отсутствии мнимой части комплексного числа:
A = K + j0 = K.
При отсутствии действительной части комплексного числа:
A = 0 ± j A// = ±A".
Следует заметить, что алгебраическая форма - более удобная форма записи комплексных чисел при их сложении и вычитании.
2. Тригонометрическая форма записи комплексных чисел является производной алгебраической формы с учетом того, что
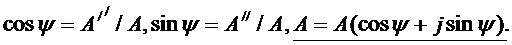
Тригонометрическая форма записи комплексных чисел наиболее удобна при переходе к алгебраической форме записи от показательной.
3. Показательная форма записи комплексных чисел является производной от тригонометрической с учетом того, что в соответствии с формулой Эйлера
где еjψ - поворотный множитель (показывает, что вектор повернут относительно вещественной оси в положительном направлении на угол ψ).
Поворотные множители j и еjψ могут быть записаны в следующем виде:
При ψ = ± π/2 в соответствии с формулой Эйлера
поэтому еjπ/2 = j; е-jπ/2 = -j.
Показательная форма записи комплексных чисел оказывается более удобной формой записи при умножении, делении, извлечении корней, логарифмировании комплексных чисел.
Таблица 1.1