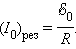Комплексным сопротивлением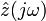 
называется отношение комплексной амплитуды напряжения гармонического сигнала, прикладываемого к двухполюснику, к комплексной амплитуде тока, протекающего через двухполюсник. При этом импеданс не должен зависеть от времени: если время t в выражении для импеданса не сокращается, значит, для данного двухполюсника понятие импеданса неприменимо.
Сопротивление — идеальный элемент обладающий только сопротивлением, ёмкость, индуктивность и токи утечки у такого элемента отсутствуют.
Импеданс Сопротивления равен
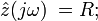
Индуктивность — идеальный элемент обладающий только индуктивностью, внутреннее сопротивление, токи утечки и ёмкость у этого элемента отсутствуют.
Импеданс Индуктивности равен
Ёмкость — идеальный элемент обладающий только ёмкостью, внутреннее сопротивление, токи утечки и индуктивность у этого элемента отсутствуют.
Импеданс Ёмкости равен
Для цепей синусоидального тока законы Кирхгофа формулируются так же, как и для цепей постоянного тока, но только для комплексных значений токов и напряжений. Первый закон Кирхгофа: «алгебраическая сумма комплексов тока в узле электрической цепи равна нулю»
Второй закон Кирхгофа: «в любом замкнутом контуре электрической цепи алгебраическая сумма комплексных ЭДС равна алгебраической сумме комплексных напряжений на всех пассивных элементах этого контура».
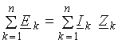
Последовательные RL, RC, RLC цепи. Полное и комплексное сопротивления, векторные диаграммы. Параллельная RLC цепь. Комплексная проводимость, векторная диаграмма.
RC
Если участок цепи содержит ряд параллельно соединенных сопротивлений, индуктивностей и емкостей, то
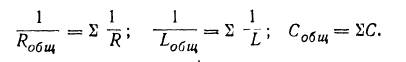
Сопротивление цепи
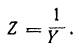, где Y - полная электрическая проводимость цепи.
|
|
Адмитта́нс (англ. admittance от лат. admittere пропускать, впускать) — полная комплексная проводимость двухполюсника для гармонического сигнала.
Стандартное обозначение адмиттанса в формулах — Y или y, единица СИ — сименс (См, S).
Резонанс в последовательной RLC-цепи. Векторная диаграмма при резонансе. Резонансная частота, характеристическое сопротивление, добротность, резонансная характеристика последовательного колебательного контура, полоса пропускания.
Явление возрастания амплитуды колебаний тока при совпадении частоты ω колебаний внешнего источника с собственной частотой ω0 электрической цепи называется электрическим резонансом. При резонансе
|
Понятие добротности RLC-контура:
|
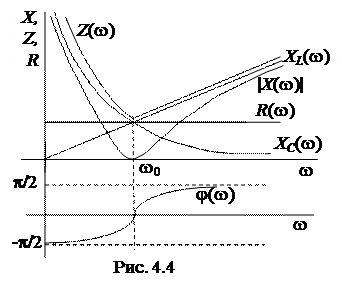
Зависимости параметров контуров RLC -контура от частоты называют частотными характеристиками. Это индуктивное сопротивление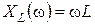 
, емкостное сопротивление 
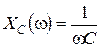, реактивное сопротивление 
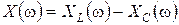, активное сопротивление 
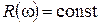, полное сопротивление
, угол сдвига фаз 
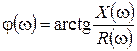. Качественный вид этих характеристик приведен на рис. 4.4.
В момент резонанса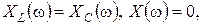 
.
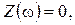
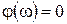Зависимости тока I (w), напряжения на индуктивности UL (w),напряжения на емкости UC (w) называют резонансными характеристиками.
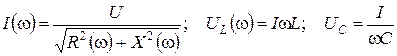. (4.7)
 
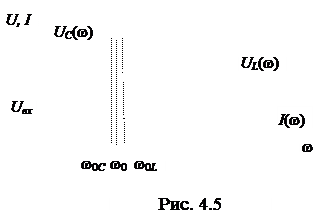
| Графики этих характеристик при добротности Q = 2 представлены на рис. 4.5. При добротности контура Q < 5 максимумы напряжений UL и UC смещаются друг от друга на одно и то же значение частоты от резонансной w0. При добротности контура Q > 5 максимумы этих напряжений при резонансной частоте w = w0сливаются. |
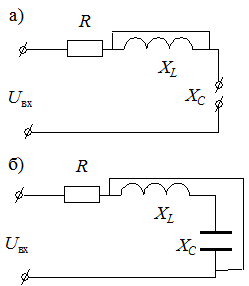Если частота w = 0, то XC = ¥, XL =0 (рис. 4.6, а). При этом условии
|
|
.
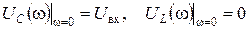Если частота равна резонансной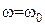 
, то X = 0 (рис. 4.6, б). При этом 
.
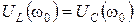Если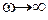 
, тогда 
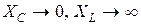(рис. 4.6, в). При этом 
.
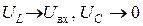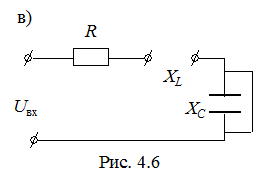Из приведенных характеристик следует, что RLC - контур обладает избирательными свойствами. Самое большое значение тока имеет место в режиме резонанса (w = w0). Для оценки избирательных свойств контура вводят понятие полосы пропускания контура. Она равна разности частот, которым соответствует отношение 
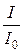до и после резонанса, равное 
.
 
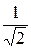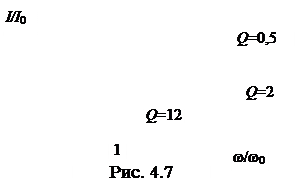
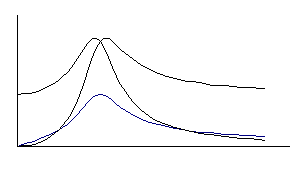
| Параметры цепи оказывают большое влияние на избирательность. Чем больше добротность контура, тем выше его избирательность. В этом можно убедиться при рассмотрении кривых на рис. 4.7
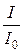( – отношение тока текущей
|
частоты к току резонансной частоты;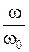 
– отношение текущей частоты к резонансной. Чем больше добротность контура, тем лучше его избирательные свойства и тем меньше полоса пропускания.
Резонанс в параллельной RLC цепи. Резонансная частота, характеристическое сопротивление, добротность, резонансная характеристика последовательного колебательного контура, полоса пропускания.
Отношение напряжения на реактивных элементах (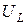
и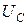 
) к напряжению на входе в режиме резонанса называют добротностью контура:
.
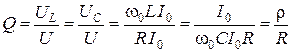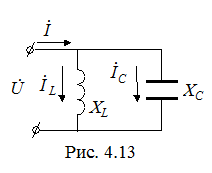В качестве частотных характеристик в контуре на рис. 4.13 выступают зависимости 
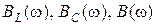, значения которых при 
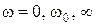приведены в табл. 4.3.
Характер изменения зависимостей 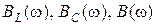приведен на рис. 4.14.
Таблица 4.3
| w |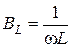 
| 
| 
|
| ¥ | ¥ | ||
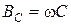
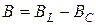
| w0 | 
| 
| |
| ¥ | ¥ | ¥ |
 |
Учитывая, что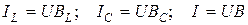 
, характер резонансных кривых 
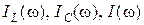полностью совпадает с соответствующими частотными зависимостями. При 
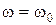такой контур выполняет роль фильтра – пробки, проводимость его, а следовательно, и ток 
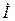общей ветви, равны нулю, а сопротивление – бесконечности.
|
|