Задача 1. Приемник энергии сопротивлением R = 20 Ом питается от аккумуляторной батареи с э.д.с E6=140 В при напряжениии на ее зажимах Uб=135 В. Емкость одного элемента батареи Q3= 36 А.ч при десятичасовом разряде; э.д.с. элемента E3 = 2,0 В. Составить схему батареи, т. е. определить количество элементов и способ их соединения; начертить схему батареи с приемником энергии. Определить внутреннее сопротивление батареи Rоб и одного элемента Rоэ.
Задача 2. Аккумуляторная батарея состоит из 10 элементов и имеет 2 параллельные группы. Э.д.с. одного элемента Eэ=1,5 В, внутреннее сопротивление Rоэ=0,03 Ом; емкость батареи Q6=54 А.ч, время разряда tр = 3 ч. К батарее подключен приемник энергии. Определить э.д.с. E6 и ток батареи I6, внутреннее сопротивление батареи Ro6,напряжение на зажимах батареи U6и сопротивление приемника энергии R.
Начертить схему батареи с приемником: энергии.
Задача 3. Приемник энергии с сопротивлением R = 6 Ом питается от аккумуляторной батареи, состоящей из 20 последовательно соединенных элементов. Э.д.с. каждого элемента Eэ = 1,25 В, напряжение при работе U3=l,2 В. Начертить схему батареи с приемником энергии. Определить э.д.с. батареи E6, напряжение U6, разрядный ток I6, внутреннее сопротивление батареи Rоб и одного элемента Rоэ, емкость элемента Q3, если продолжительность разряда t = 7 ч.
Задача 4. Рассчитать батарею щелочных аккумуляторов, т. е. определить число элементов и составить схему ее соединения для питания приемника энергии мощностью Р=0,5 кВт при напряжении U=60 В, если э.д.с. одного элемента Eэ=1,6 В. внутреннее сопротивление Rоэ = 0,02 Ом; емкость Q»=28 А.ч, время разряда t=6 ч. Определить э.д.с. Eэ внутреннее сопротивление Rоб.
Задача 5. Аккумуляторная батарея автомобиля состоит из п = 6 последовательно соединенных элементов. Емкость одного элемента Qэ = 42 А.ч, время разряда t=l0 ч. Э.д.с. батареи E6=12,5 В, номинальное напряжение батареи Q6 = 12 В. Начертить схему Старей. Определить ток батареи Iб, внутреннее сопротивление батареи Rоб и одного элемента Rоэ, э.д.с. элемента £э. Определить ток Iкэ при коротком замыкании на зажимах батареи.
Задача 6. Цилиндрическая (прямая) катушка длиной l = 7,5 cм намотана на эбонитовом каркасе. Ток в катушке I = 10A, напряженность магнитного поля по осевой линии катушки H = 2000 А/м. Определить число витков катушки 
и магнитную индукцию В по осевой линии катушки. Начертить катушку и, задавшись направлением тока, показать направление вектора магнитной индукции на осевой линии катушки.
Задача 7. Кольцевая катушка, намотанная на текстолитовом каркасе, имеет число витков =100. Внутренний радиус катушки R1 = 8 см, внешний R2= 12 см. Магнитная индукция по осевой (средней) линии катушки В = 4 ·10-3Т.
Определить ток I в катушке и напряженность магнитного поля Н по осевой линии катушки. Начертить кольцевую катушку и, задавшись направлением тока в ней, показать направление векторов В и Н.
Задача 8. Прямолинейный проводник с током I=15 А создает в точке А напряженность магнитного поля H = 47,7 А/м.
Вычислить расстояние x от оси провода до точки А. Определить магнитную индукцию В в данной точке поля. Среда—воздух. Начертить проводник. Задавшись направлением тока в проводнике, показать.направление вектора В в точке А.
Задача 9. Цилиндрическая (прямая) катушка имеет число витков = 300, длину l=5 см, намотана на текстолитовом каркасе. Ток в катушке I=0,5 А. Определить напряженность Н и магнитную индукцию В по осевой линии катушки. Начертить катушку и, задавшись направлением тока в ней, показать направление векторов В и Н.
Задача 10. Кольцевая катушка имеет число витков =500, намотана кермаческом каркасе. Внутренний радиус катушки R1=.13 см, внешний R2=17 см. Ток в катушке I=10А. Определить напряженность магнитного поля Н и магнитную индукцию В по осевой (cредней) линии катушки. Начертить катушку и, задавшись направлением тока в ней, показать направление вектора магнитной индукции.
Задача 11. Три провода расположены параллельно в одной плоскости (рис. 28). Расстояние между опорами l=10 м,. а между осями проводов а=0,5 м. Среда — воздух. В режиме короткого замыкания в проводах возникают токи I1=200 А, I2= 300 А, I3 = 400 А. Направление токов указано на рис. 28. Рассчитать силы взаимодействия каждой пары проводов с токами, векторы этих сил в масштабе показать на схеме.
Определить результирующие силы, действующие на каждый 'провод и в масштабе показать их векторы на схем
Задача 12. В вершинах равностороннего треугольника со стороной а=2 м расположены три провода с токами I1=600 А, I2 = 700 А, I3=800 А. Направление токов указано на рис. 29. Расстояние между опорами для крепления проводов l=50 м. Среда — воздух.
Рассчитать силы взаимодействия каждой пары проводов, векторы этих сил в масштабе показать на схеме.
Графическим способом определить результирующую силу F3, действующую напровод с током I3.
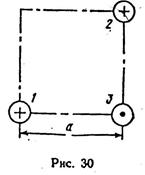
3адача 13. Три провода расположены в трех вершинах квадра. Сторона квадрата а=1 м. Токи в проводах равны I1 =900 А, I2 =1000 А, I3=1200 А. Направление токов указано на рис. 30. Провода находятся в воздухе. Расстояние между опорными изоляторами проводов l=5 м.
Рассчитать силы взаимодействия каждой пары проводов и показать в масштабе векторы этих сил на схеме. Графическим способом определить результирующую силу F1, действующую на провод с током I1.
Задача 14. По трем жилам кабеля, расположенным в вершинах равностороннего треугольника со стороной а=15мм, проходят токи
I1= I2=I3 600 А.
Направление токов указано на рис. 31. Относительная. магнитная, проницаемость изоляции кабеля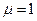 
. Рассчитать силы взаимодействия, каждой пары жил кабеля; и показать масштабе инвесторы на схеме.
Определить графическим способом результирующие: силы, действующие на каждый метр (l=1м) жил, кабеля.
Задача15. Три провода расположены в трех вершинах квадрата. Токи в проводах I1 = 1200 А, I2 = 1000 А. I3 =1500 А. Направление токов указано на рис. 32. Провода находятся в воздухе. Сторона квадрата а=1,5 м. Расстояние между опорными изоляторами проводов l=6 м.
Рассчитать силы взаимодействия каждой пары проводов и показать в масштабе векторы этих сил на схеме. Графиче6ским способом определить результирующую силу F3, действующую на провод с током I3.
Задача 16. На рис. 33 изображен тороидальный электромагнит. Сердечник выполнен из электротехнической стали, и имеет воздушный зазор. Размеры сердечника в мм проставлены на рис. 33. Определить ток, I, который должен проходить по обмотке для создания в сердечнике магнитного потока Ф=1,02∙10- 4 Вб. Число витков обмотки 
=200. Вычислить также, какой ток I′ должен ′проходить по обмотке для создания заданного магнитного потока, если в сердечнике будет отсутствовать воздушный зазор. Кривая намагничивания электротехнической стали приведена на рис. 50.
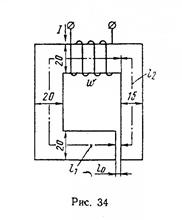
Задача 17. Магнитопровод выполнен из электротехнической стали (рис. 34) и имеет воздушный зазор. Размеры сердечника по средней магнитной линии l = 160 мм; l 2 = 80мм, l 0=20 мм. Толщина сердечника 20 мм.
Определить число витков катушки ,необходимое для создания в магнитопроводе магнитного потока Ф=5,4∙10- 4 Вб, если по катушке будет проходить ток I = 5,5 А.
Какое число витков катушки ′ потребуется при тех же условиях, если в сердечнике будет отсутствовать воздушный зазор?
Кривая намагничивания электротехнической стали приведена на рис. 50.
Задача 18. Магнитопровод выполнен из электротехнической стали и имеет два воздушных зазора (рис. 35). Размеры магнктопровода по средней магнитной линии: l 1=140 мм, l 2= 110 мм, l 01= l 02 = 0,1 мм. Толщина сердечника 30 мм.
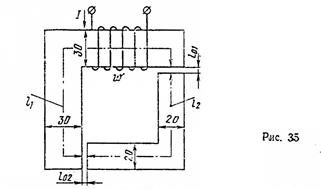
В стержне, на котором расположена обмотка, требуется создать магнитную индукцию B 1=0,9 Т. Определить ток I, который необходимо пропустить по обмотке, чтобы создать заданную магнитную индукцию, если обмотка имеет =100 витков.
Кривая намагничивания электротехнической стали приведена на рис. 50.
Задача 19. Магнитопровод выполнен из электротехнической стали и имеет два воздушных зазора (рис. 36). Размеры магнитопровода поо средней магнитной линии: l 1= 100 мм, l 2=180 мм, l 01= l 02=1 мм. Толщина сердечника 50 мм. Определить число витков катушки , необходимое для создания в магнитопроводе магнитного штока Ф =15∙10- 4 Вб, если по катушке будет проходить ток I =5 А.
Какое число витков катушки ' потребуется при тех же условиях, если в сердечнике будет отсутствовать воздушный зазор?
Кривая намагничивания электротехнической стали приведена на рис. 50.
Задача 20. На рис. 37 изображен магнитопровод из электротехнической стали с воздушным зазором. Размеры сердечника то средней магнитной линии: l 1= 150 мм, l 2= 75 мм, l 0=1,5 мм. Тощина сердечника 40 мм. В стержне, на котором расположена обмотка, требуется создать магнитную индукцию B 1=l Т. Определить ток, который нужно пропустить по обмотке, чтобы создать заданную магнитную индукцию, если обмотка имеет = 500 витков. Какой ток I' нужно будет пропустить по обмотке для создания той же магнитной индукции В, если число витков обмотки увеличить
вдвое. Кривая намагничивания электротехнической стали приведена на рис. 50.
Задача 21. В однородном магнитном поле с индукцией B = 1,5 Т перпендикулярно силовым линиям поля под действием внешней силы F движется проводник АБ со скоростью 
=10 м/с (рис. 38). Проводник имеет длину l =50 см и сопротивление R 0 = 0,5 Ом. К концам проводника присоединено сопротивление R=2 Ом.
Определить э.д.с. E, наводимую в проводнике; ток I в цепи; тормозную электромагнитную силу F т. Составить уравнение баланса мощностей цепи. Показать на схеме направление векторов э.д.с. Е, тока I и тормозной силы F т. Указать, по каким правилам определены направления этих векторов.
Задача 22. Проводник АБ длиной l =50 см (рис. 39), обладающий сопротивлением R0= 2 Ом, присоединен к зажимам источника питания с напряжением U = 20 В. Провод находится в однородном магнитном поле с индукцией B = 1,6 Т. Вследствие взаимодействия тока с этим полем провод перемещается перпендикулярно магнитным силовым линиям со скоростью . Ток в движущемся проводнике I= 6А.
Определить силу F, действующую на движущийся проводник; наведенную в проводнике э. д. с. Е; скорость движения проводника (рабочий режим).
Определить ток I п и силу F п, действующую на неподвижный проводник (пусковой режим). Составить уравнение баланса мощностей цепи. Показать на схеме направления векторов тока I, э.д.с. Е и силы F и указать правила, по которым определены их направления.
Задача 23. В однородном магнитном поле (рис. 38) с магнитной индукцией В = 2 Т перпендикулярно силовым линиям поля движется проводник АБ длиной l = 75 см, сопротивлением R0 = 0,2 Ом и током I= 2 А. Проводник замкнут на сопротивление R =2,8 Ом. Определить э. д. с. Е, скорость его движения , электромагнитную тормозную силу F т; составить уравнение баланса мощностей цепи. На схеме показать направление векторов э.д.с. тока I и электромагнитной тормозной силы E т. Указать правила, по которым определены их направления.
Задача 24. В однородном магнитном поле с магнитной индукцией В =1,2 Т, перпендикулярно к его направлению со скоростью =15 м/с перемещается проводник АБ длиной l = 80 см. (рис. 39). Проводник присоединен к источнику питания напряжением U=25 В и имеет сопротивление R0=2 Ом. Определить наводимую противо-э. д. с. Е, ток в движущемся проводнике I, электромагнитную силу F, ток пускового режима I п( =0). Составить уравнение баланса мощностей цепи. На схеме показать направление векторов противо-э. д. с. тока и электромагнитной силы. Указать правила, по которым определены их направления.
Задача 25. В однородном магнитном поле (рис. 38) с магнитной индукцией В=0,8 Т перпендикулярно силовым линиям поля со скоростью =12 м/с движется проводник длиной l=1м сопротивлением R0 = 0,4 Ом. Проводник замкнут на сопротивление R = 3,6 Ом. Определить э.д.с. Е, наводимую в проводнике; тормозную электромагнитную силу F т и составить уравнение баланса мощностей пели. Указать правила, по которым можно определить направления Е, I, F ти показать на схеме направления их векторов.
Задача 26. Кольцевая катушка выполнена на текстолитовом каркасе (без сердечника) и имеет =1200 витков. Средний радиус катушки R ср = 5 см; площадь поперечного сечения S=20 см2 (рис.40).
По катушке проходит ток, нарастающий с равномерной скоростью, при этом в катушке наводится э. д. с. самоиндукции 
= 2,3 В. Начертить катушку. Определить ее индуктивность L и скорость нарастания тока 
.
Задача 27. Две катушки равномерно намотаны на одном кольцевом текстолитовом каркасе (без сердечника). Ток в
первой катушке нарастает с равномерной скоростью =
250 
, при этом во второй катушке наводится э. д. с. взаимоиндукции 
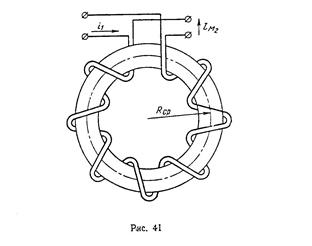
=−5 В. Средний радиус каркаса R ср= 5 см, площадь поперечного сечения S=10 см2, число витков второй катушки 2=1300. (рис. 41).
Начертить катушки и определить их взаимную индуктивность M.
Зная взаимную индуктивность, рассчитать число витков первой катушки 1.
Задача 28. Ток в цилиндрической катушке (рис. 42) без ферромагнитного сердечника нарастает с равномерной скоростью =150 А/с; при этом в катушке наводится э. д. с. самоиндукции 
=−3В. Длина катушки l = 8 см и площадь поперечного сечения ее S=24 cм2.
Начертить катушку и определить ее индуктивность L. Рассчитать число витков катушки .
Задача 29. Определить взаимную индуктивность М двух катушек, намотанных равномерно на одном цилиндрическом текстолитовом каркасе (без сердечника), если известно: число витков катушек 1=2000; 2=1000; длина каркаса l = 4 см, площадь поперечного сечения S = 6 см2 (рис. 43).
Начертить катушки. Определить э. д. с. взаимоиндукции ем2, наведенную во второй катушке, если в первой катушке ток убывает с равномерной скоростью di 1/ dt = 240А/с.
Задача 30. Кольцевая катушка равномерно намотана на текстолитовом каркасе (без сердечника). Средний радиус катушки R ср =3 см, число витков = 1500 (рис. 40).
Начертить катушку. Вычислить площадь поперечного сечения катушки S, если она обладает индуктивностью L = 12 мГн.
Определить, какая э. д. с. самоиндукции eLнаведется в катушке при равномерном нарастании тока со скоростью di / dt =200 А/с.
Ответы к задачам контрольной работы № 2
1. Rоэ = 0,021 Ом
2. Rоб = 0,075 Ом
3. Qэ = 28 А.ч
4. Е6= 64В
5. I кз=105 А
6. =150 витк
7. I =20 А
8. ВА = 6∙10−5 Т
9. H =3000 
l0. Вср = 6,7∙10−3 Т
11. F 1= 0,4 Н
12. F 13 = 2,4 Н
13. F 12 = 0,64 Н
14. F 3 = 5,77 Н
15. F 23 = 1,2 Н
| 16. I = 6,3 А
17. ' = 198 витк
18. I = 3,98 А
I9. = 337 вита
20. I' =1,3 А
21. I = 3 А
22. F Р = 4,8 Н
23. F T=3 Н
24. I =5,3 А
25. E = 9,6 В
26. di / dt = 200 А/с
27. 1=3846 витк
28. L = 20 мГ
29.  =−9,05 В
30. =−2,4 В
|
Методические указания
к выполнению домашней контрольной работы № 2
Для решения задач 1–5 необходимо изучить тему 2.5 «Химические источники электрической энергии».
Химические источники тока соединяются в батарею, когда потребитель электрической энергии требует больший ток и большее напряжение, чем может дать один элемент.
Соединение в батарею допускается только для элементов, имеющих одинаковую емкость Qэ, одинаковую э.д.с. Еэ и одинаковое внутреннее сопротивление Rоэ.
Пример 9
Рассчитать батарею кислотных аккумуляторов, т. е. определить число элементов и составить схему ее соединения для питания приемника энергии мощностью Р =1 кВт при напряжении U =110 В, если э. д. с. одного элемента Е э = 2 В, внутреннее сопротивление Rоэ = 0,05 Ом, емкость Qэ = 30 А.ч. время разряда t =5 ч. Определить э.д.с. Е би внутреннее сопротивление R об.
Решение
1. Ток приемника энергии
А.
2. Разрядный ток одного элемента
A/
3. Количество параллельных групп батареи
, принимаем m =2
4. Требуемое число последовательно соединенных элементов п можно найти из формулы закона Ома:
; 
где 
; 
; 
; 
;
;
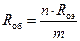подставим известные величины
n и найдем n
2 n –0,23 n =110; 1,77 n =110; 
;
принимаем n =63 элемента.
5. Общее число элементов 'батареи
N=n∙m= 63∙2=126 эл.
6. Э.д.с. батареи
Е э = n∙Е б =126 В.
7. Внутреннее сопротивление батареи
Ом
8. Вычерчиваем схему батареи (рис. 44).
Для решения задач 6–10 должен быть изучен материал темы 3.1 «Магнитное поле». В этих задачах рассматривается магнитное поле (прямолинейного проводника с током, а также магнитное толе кольцевой или цилиндрической катушки с током.
Пример 10
По прямолинейному проводу воздушной линии проходит ток I =600 А. Определить напряженность магнитного ноля Н и магнитную индукцию В в точке М, расположенной от проводника на расстоянии х =0,5 м. Начертить проводник. Задавшись направлением тока в проводе, показать направление векторов В и Н в точке М.
Решение
1. Вычерчиваем схему (рис. 45), задаемся направлением тока в проводе и, применяя правило буравчика, определяем направление магнитной силовой линии, проходящей через, заданную точку М. Векторы напряженности поля Н и магнитной индукции В в точке М направлены по касательной к магнитной силовой линии; их направление совпадает с направлением магнитной силовой линии.
2. По закону.полного тока напряженность магнитного доля в точке М
3. Магнитная индукция в точке М
Т.
где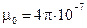 
– магнитная проницаемость вакуума
(магнитная постоянная);
– относительная магнитная проницаемость среды, в которой находится провод (для воздуха =l).
Пример 11
Кольцевая катушка намотана на каркасе из немагнитного материала. Внутренний радиус катушки R 1=1,8 см, внешний R 2=2,6 см. Напряженность магнитного поля по средней магнитной линии катушки H = 3617 ; ток в катушке I = 10А. Определить число витков катушки и магнитную индукцию В по средней линии катушки. Начертить катушку и, задавшись направлением тока в ней, показать направление векторов В и H.
Решение
1. Вычерчиваем схему кольцевой катушки (рис. 40); задаемся направлением тока в катушке и, применяя правило буравчика, определяем направление магнитной силовой линии, имеющей радиус R cp; это же направление будут иметь векторы В 'и H на осевой (средней) линии катушки (в любой точке осевой магнитной линии они направлены по касательной к ней).
2. Индукция магнитного поля по средней линии катушки
Т,
где 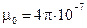Г/м– магнитная постоянная;
=1–относительная магнитная проницаемость немагнитного материала сердечника катушки.
3. Число витков катушки найдем из формул напряженности магнитного.поля по средней магнитной линии 
, предварительно определив Rср:
Пример 12
Цилиндрическая катушка имеет число витков = 250, длину l = 6 см, намотана на керамическом каркасе. Ток в катушке I = 3,6 А. Определить напряженность H и магнитную индукцию В по осевой линии катушки. Начертить катушку и, задавшись направлением тока в ней, показать направление векторов В и H.
Решение
1. Вычерчиваем схему цилиндрической (прямой) катушки (рис.42). Задаемся направлением тока в катушке и, применяя правило буравчика, определяем направление магнитной силовой линии, совпадающей с осевой линией катушки, показываем в этом направлении векторы В и H.
2. По закону полного тока напряженность магнитного поля по осевой линии прямой.катушки
3. Магнитная индукция прямой катушки
Т,
где 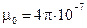Г/м – магнитная постоянная,
– относительная магнитная проницаемость немагнитного материала сердечника катушки.
Задачи 11 –15 посвящены расчету электромагнитных сил, действующих на параллельные провода с токами (Частоедов, § 7.6).
Пример 13
При коротком замыкании токи в шинах электростанции (рис. 46) достигли значений I 1 = 10000 А, I 2 =5000 А, I 3 =5000 А. Шины расположены параллельно друг другу, расстояние между осями шин а =125 мм, между опорными изоляторами l =1 м. Среда – воздух. Рассчитать силы взаимодействия каждой пары шин при длине l =1 м; векторы этих сил в масштабе показать на схеме. Определить результирующие силы, действующие на опорные изоляторы и в масштабе показать их на схеме.
Решение
Находим силы взаимодействия для каждой пары шин отдельно при длине l =1 м.
Сила взаимодействия между первой и второй шинами
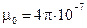где Г/м – магнитная «постоянная;
— относительная магнитная проницаемость среды, в которой находятся шины; согласно условию среда – воздух, следовательно, ;
I 1, I 2 – токи в шинах в А,
а —расстояние между шинами в м,
l — длина шин (расстояние между точками крепления) в м.
Сила взаимодействия между второй и третьей шинами
Сила взаимодействия между первой и третьей шинами
2. Вычерчиваем схему расположения шин (поперечное сечение) и показываем направление токов в шинах (рис. 47).
Определим направление сил взаимодействия шин с токами: шины с токами одного направления притягиваются друг к другу, а с токами противоположного направления отталкиваются.
Покажем согласно этому правилу на рис. 47 в масштабе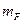 
=80 H/см векторы сил F 12, F 23, F 13.
3. Определим результирующие силы, действующие на опорные изоляторы. Как видно из рис. 47, на каждый изолятор первой шины действуют две силы F 12и F 13, направленные в противоположные стороны. Результирующая сила, действующая на опорный изолятор, первой шины, равна их разности и совпадает по направлению с F 12
F 1 = F 12 – F 13= 80−40= 40 Н.
На изолятор второй шины действуют две силы F 12 и F 23, направленные в противоположные стороны. Результирующая сила, действующая на опорный изолятор, равна их разности и совпадает по направлению с F 12
F2 = F 12– F 23= 80–40= 40 Н.
На изолятор третьей шины действуют две силы F 13 и F 23, направленные в противоположные стороны. Результирующая сила, действующая на опорный изолятор третьей шины, равна нулю
F 3 = F 23– F 13= 40–40= 0.
Векторы сил F 1, F 2, F 3покажем в масштабе на схеме (рис.47).
Если проводники с токами расположены не в одной плоскости а, например, в вершинах квадрата, то расчет сил взаимодействия проводов с токами проводится также для каждой пары проводов отдельно, и векторы всех сил в масштабе подзываются на схеме (рис. 48):
Векторы результирующих сил, действующих на каждый провод, определяют графически, как сумму векторов всех сил, действующих на данный провод. Чтобы определить величину каждой результирующей силы, необходимо измерить длину вектора этой силы и умножить его на масштаб. Например, F 1= l F1∙ m F.
В задачах 16–20 предусматривается выполнение расчета магнитной цепи.
Расчет неразветвленной магнитной цепи в большинстве случаев сводится к определению намагничивающей силы I∙ , которая требуется для получения заданного магнитного потока Ф или магнитной индукции В. При этом указываются размеры и материал всех участков магнитной цепи.
Приступая к расчету магнитной цепи, следует разделить ее на участки, каждый из которых должен иметь по всей длине одинаковое сечение и одинаковый материал. За длины участков принимаются соответствующие длины средней магнитной линии.
Пример 14
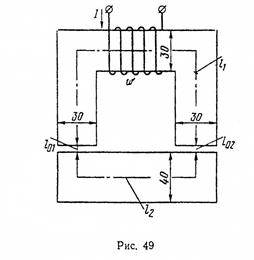
Магнитопровод выполнен из электротехнической стали и имеет два воздушных зазора (рис. 49). Размеры магнитопровода по средней магнитной линии: l 1 = 240 мм, l 2=20 мм, l 01 = l 02=l мм. Толщина сердечника 40 мм.
В стержне, на котором расположена обмотка, требуется создать магнитную индукцию B 1 = l,lТ. Определить магнитный поток Ф в данной магнитной цепи. Найти ток I, который необходимо пропустить по обмотке, чтобы создать заданную магнитную индукцию B. Обмотка имеет = 50 витков.
Какой ток I' нужно пропустить по обмотке, чтобы создать заданную магнитную индукцию, если в сердечнике будет отсутствовать воздушный зазор?
Кривая намагничивания электротехнической стали приведена на рис. 50.
Решение
1. Разобьем магнитную цепь на участки, каждый из которых должен иметь по всей длине одинаковое сечение и одинаковый материал. В данной магнитной цепи таких участка четыре:
два участка из электротехнической стали, их длина и сечение
l 1=240 мм = 24 см; S 1=30∙40 = 1200 мм2 =12∙10–4 м2;
l 2=120 мм = 12 см; S 2=40∙40 = 1600 мм2 =16∙10–4 м2;
два воздушных зазора, их длина и сечение
l 01= l 02= 1 мм = 0,1 см; S 01= S 02= S 1=12∙10–4 м2;
2. Магнитный поток в данном магнитопроводе
Ф = B 1∙ S 1=1,1∙12∙10–4=13,2∙10–4 Вб.
3. Поскольку магнитный поток в данном неразветвленyом магнитопроводе Ф = const, определим магнитную индукцию на втором участке из электротехнической стали
T.
4. Магнитная индукция в воздушных зазорах B 01= B 02= B 1= 1,1 T, т.к. S 01= S 02= S 1/.
5. Напряженность магнитного поля для участков из электротехнической стали находим по кривой первоначального намагничивания (рис. 50)
при B 1= 1,1 T, H 1=4,5 A/см,
при B 2= 0,825 T, H 2=2,4 А/см.
6. Напряженность магнитного поля в воздушных зазорах находим по формуле
H 01= H 02=0,8∙ B 01∙104=0,8∙1,1∙104 = 8800А/см.
7. По закону полного тока I ∙ = 
находим ток в обмотке
8. Если в. сердечнике будут отсутствовать воздушные зазоры, то ток в обмотке
В задачах 21–25-рассматривается явление электромагнитной индукции в прямолинейном проводнике, перемещающемся в магнитном поле; принцип работы электрического генератора и двигателя. Для успешного решения этих задач следует изучить тему 3.3. «Электромагнитная индукция».
Пример 15
В однородном магнитном поле с индукцией В =1,3 Т перпендикулярно к направлению магнитных силовых линий движется проводник АБ длиной l =90 см со скоростью =20 м/с
(рис. 51). Проводник -замкнут на внешнее сопротивление R=3,7Ом, сопротивление самого проводника R 0==0,3 Ом.
Определить э. д. с. наводимую в проводнике, ток I в цели и электромагнитную тормозную силу Ft, действующую на проводник. Направление, векторов Е, I, Ft –показать на схеме. Указать правила, по которым определены направления этих векторов.
Составить уравнение баланса мощностей цепи.
Решение
1. Согласно закону электромагнитной индукции в проводнике наводится э. д. с
где 
= 
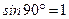(проводник движется перпендикулярно, силовым линиям магнитного поля).
Направление э. д. с. индукции E определяется по правилу правой руки (показано на рис. 51).
2. Под действием э.д.с. Е в цепи возникает ток
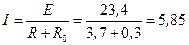A.
Направление тока I совпадает с направлением э. д. с.
E– генераторный режим. Покажем направление тока на рис.51
3. Магнитное поле действует на проводник с током I cсилой
Н
Направление силы 
определяется правилом левой руки − показано на рис. 51. Очевидно, что электромагнитная сила носит тормозной характер. Следовательно, при равномерном движении проводника внешняя механическая сила должна преодолевать действие 
, т. е. 
.
4.Составим уравнение баланса мощностей цепи:
механическая мощность внешней силы
эта мощность преобразуется в электрическую 
, а затем в тепловую
Уравнение баланса мощностей цепи имеет вид
В разобранном примере проводник работает в режиме генератора. Рассмотрим пример, в котором проводник будет работать в режиме двигателя.
Пример 16
Прямолинейный проводник АБ длиной l= 0,5 м и источник энергии с напряжением U =10 В соединены проводами, сопротивление которых равно нулю (рис. 52).
В результате взаимодействия с однородным магнитным тюлем проводник движется перпендикулярно направлению поля с равномерной скоростью =10 м/с. Магнитная индукция В= 1,4Т, сопротивление проводника R 0=0,1 Ом.
Найти ток I в цепи и силу F, под действием которой проводник движется, а также пусковой ток I п.
Направление векторов Е, I и F показать на схеме. Указать правила, по которым определены направления этих векторов. Составить уравнение баланса мощностей цепи.
Решение
1. Под де