Даны N упорядоченных множеств U1, U2,..., UN (N - известно), и требуется построить вектор A=(a1, a2,..., aN),
где a1ÎU1, a2ÎU2,..., aNÎUN, удовлетворяющий заданному множеству условий и ограничений.
|
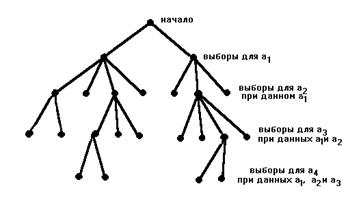
В алгоритме перебора вектор А строится покомпонентно слева направо. Предположим, что уже найдены значения первых
(k-1) компонент, А=(а1, а2,..., а(k-1),?,...,?), тогда заданное множество условий ограничивает выбор следующей компоненты аk некоторым множеством SkÌUk.
Если Sk<>[ ] (пустое), мы вправе выбрать в качестве аk наименьший элемент Sk и перейти к выбору (k+1) компоненты и так далее.
Однако если условия таковы, что Sk оказалось пустым, то мы возвращаемся к выбору (k-1) компоненты, отбрасываем а(k-1) и выбираем в качестве нового а(k-1) тот элемент S(k-1), который непосредственно следует за только что отброшенным.
Может оказаться, что для нового а(k-1) условия задачи допускают непустое Sk, и тогда мы пытаемся снова выбрать элемент аk. Если невозможно выбрать а(k-1), мы возвращаемся еще на шаг назад и выбираем новый элемент а(k-2) и так далее.
Графическое изображение - дерево поиска. Корень дерева
(0 уровень) есть пустой вектор.
Его сыновья суть множество кандидатов для выбора а1, и, в общем случае, узлы k-го уровня являются кандидатами на выбор аk при условии, что а1, а2,..., а(k-1) выбраны так, как указывают предки этих узлов. Вопрос о том, имеет ли задача решение, равносилен вопросу, являются ли какие-нибудь узлы дерева решениями. Разыскивая все решения, мы хотим получить все такие узлы.
Задача о лабиринте
Классическая задача. Дано клеточное поле, часть клеток занята препятствиями. Необходимо попасть из некоторой заданной клетки в другую заданную клетку путем последовательного перемещения по клеткам. Изложение задачи опирается на рисунок произвольного лабиринта и две «прорисовки» с использованием простого перебора и метода «волны».
Классический перебор выполняется по правилам, предложенным в 1891 г. Э. Люка в “Математических досугах”:
· в каждой клетке выбирается еще не исследованный путь;
· если из исследуемой в данный момент клетки нет путей, то возвращаемся на один шаг назад (в предыдущую клетку) и пытаемся выбрать другой путь.
Естественными модификациями задачи поиска всех путей выхода из лабиринта являются:
· поиск одного пути;
· поиск одного пути кратчайшей длины методом «волны».
·
Решение первой задачи.
int main()
{
constint Nmax=...;
int intdx[4] = {1, 0, -1, 0};
int dy[4] = {0, 1, 0, -1};
int A[Nmax+1][Nmax+1];
int xn, yn, xk, yk, N;
Init(A, …);
Solve(A, xn,yn,xk, yk,1);
}
// Функция Init();
//
// <Ввод лабиринта, координат начальной и конечной клеток.
// Границы поля отмечаются как препятствия>;
//Функция output (intA[][Nmax+1], …);
....
{
<вывод матрицы А - метками выделен путь выхода из лабиринта>;
}
void Solve(int A[][Nmax+1], int x, int y, intxk, intyk, int k)
// k - номершага,
//x, y - координатыклетки
{
inti;
A[x][y] = k;
if ((x==xk) && (y==yk)) output(A,m,n);
else
for(i=0; i< 4; i++)
if (A[x+dx[i]][y+dy[i]]==0)
Solve(A, x+dx[i],y+dy[i],k+1);
A[x][y]=0;
}
Задача о парламенте
На острове Новой Демократии каждый из жителей организовал партию, которую сам и возглавил. К всеобщему удивлению, даже в самой малочисленной партии оказалось не менее двух человек. К сожалению, финансовые трудности не позволили создать парламент, куда вошли бы, как предполагалось по Конституции острова, президенты всех партий.
Посовещавшись, островитяне решили, что будет достаточно, если в парламенте будет хотя бы один член каждой партии.
Помогите островитянам организовать такой, как можно более малочисленный парламент, в котором будут представлены члены всех партий.
Исходные данные: каждая партия и ее президент имеют один и тот же порядковый номер от 1 до N (4£N£150). Вам даны списки всех N партий острова Новой Демократии. Выведите предлагаемый Вами парламент в виде списка номеров ее членов. Например, для четырех партий:
| Президенты | Члены партий |
| 2,3,4 | |
| 1,4,2 | |
Список членов парламента 2 (состоит из одного члена).
Решение задачи - полный перебор всех вариантов. Покажем, что ряд эвристик позволяет сократить перебор для некоторых наборов исходных данных.
Представим информацию о партиях и их членах с помощью следующего зрительного образа - таблицы. Для примера из формулировки задачи она имеет вид:
|
Тогда задачу можно переформулировать следующим образом. Найти минимальное число столбцов, таких, что множество единиц из них “покрывают” множество всех строк. Очевидно, что для примера это один столбец - второй. Поговорим о структурах данных.
constintNmax=150;
intNint; //0..Nmax+1;
Sset=Set of 0..Nmax;
structPerson{
intman; // 0..Nint_1 //номержителя
intnumber; // числопартий, которыеонпредставляет
Sstepart; //партии
}
struct Person A[Nint];
Логикаформирования исходных данных (фрагмент реализации).
functionNum(S:Sset):Nint;{подсчитывает количество элементов в множестве}
vari,ch:Nint;
beginch:=0;
for i:=1 to N do if i in S then Inc(ch);
Num:=ch;
end;
procedureInit;{предполагается, что данные корректны и во входном файле они организованы так, как представлены в примере из формулировки задачи}
....
begin
.....
readln(N);{числожителей}
for i:=1 to N do with A[i] do begin man:=i; part:=[i]; end;{каждыйжительпредставляетсвоюпартию}
for i:=1 to N do begin
whileNot eoln do begin read(t);A[t].part:=A[t].part+[i];{жительtпредставляетпартиюсномеромi, илипартиясномеромiпредставленажителем t}
end;
readln;
end;
for i:=1 to N do A[i].number:=Num(A[i].part);
....
end;
Следующим очевидным шагом является сортировка массива А по значению поля number. Становится понятным и необходимость ввода поля man в структуру записи - после сортировки номер элемента массива А не соответствует номеру жителя острова.
Пока не будем задумываться о том, как сократить перебор. Попытаемся набросать общую схему. Используемые переменные достаточно очевидны, они описываются в процессе их ввода, присвоение начальных значений глобальным переменным осуществляется в процедуре Init.
procedure Include(k:Nint);{включениеврешение}
begin
Rwork:=Rwork+[A[k].man];
Inc(mn);
end;
procedure Exclude(k:Nint);{исключитьизрешения}
begin
Rwork:=Rwork-[A[k].man];
Dec(mn);
end;
procedure Solve(k:Nint;Res,Rt:Sset);
{k- номер элемента массива А; Res - множество партий, которые представлены в текущем решении; Rt - множество партий, которые следует “покрыть” решением; min - минимальное количество членов в парламенте; mn - число членов парламента в текущем решении; Rbest - минимальный парламент; Rwork - текущий парламент; первый вызов - Solve(1,[],[1..N])}
var i:Nint;
begin
| блокобщихотсечений |
ifRt=[] then begin if nm<min then
begin min:=mn;Rbest:=Rwork end;
end
else begin
i:=k;
whilei<=N do begin
| блокотсеченийпоi |
Include(i);
Solve(i+1,Res+A[i].part,Rt-A[i].part);
Exclude(i);
Inc(i);
end;
end;
end;
Итак, а что же дальше? Очевидно, что приведенная схема решения работает только для небольших значений N, особенно если есть ограничения (а они всегда есть) на время тестирования задачи. Предварительная обработка (до первого вызова процедуры Solve), заключающаяся в проверке, есть ли жители, которые представляют все партии (это первый шаг).
procedureOne(t:Nint;Q:Sset);{проверяет - есть ли среди первых t элементов массива А такой, что A[i].part совпадает с Q}
var i:Nint;
begin
i:=1;
while (i<=t) and (A[i].part<>Q) do Inc(i);
ifi<=t then begin Rbest:=Rbest+[i]; Rt:=[] end;
end;
Первый вызов этой процедуры - One(N,[1..N]), осуществляется в блоке предварительной обработки.
|
Рассмотрим пример.
| Президенты | Члены партии |
| 2,3 | |
Идея. Третий жительсостоит в партиях 1 и 3, второй - в 1, 2 и 3. Есть “вхождение”, третий житель менее активный, исключим его. Однако из примера проглядывает и другая идея - появилась строка, в которой только одна единица. Мы получили “карликовую” партию, ее представляет один житель, заметим, что первоначально, по условию задачи, таких партий нет. Житель, представляющий “карликовую” партию должен быть включен в решение, но он же активный и представляет еще другие партии. Значит, эти партии представлять в парламенте нет необходимости - они представлены. Исключаем эти партии (строки таблицы), но после этого возможно появление других “карликовых” партий. Рассмотрим этот процесс на следующем примере: 1 - 8,9; 2 - 10,11; 3 - 12, 13; 4 - 8,9,10; 5 - 11,12,13; 6 - 8,9,10,11; 7 - 9,10,11,12,13;8 - 1,4,6; 9 - 1,4,6,7; 10 - 2,4,6,7; 11 - 2,5,6,7; 12 - 3,5,7; 13 - 3,5,7; 14 - 8; 15 - 9; 16 - 10; 17 - 11; 18 - 12; 19 - 13.
Выполняя операцию исключения жителей, «представительство» которых скромнее, чем у оставшихся, получаем.
Итак, партии с 14-й по 19-ю «карликовые», их представляют жители с 8-го по 13-й. Мы обязаны включить этих жителей в парламент. Включаем. Формируем множество партий, которые они представляют. Оказывается, что все. Решение найдено без всякого перебора.
Вывод - перебор следует выполнять не по всем жителям и не для всех партий! Если бы это выручало всегда. Сверхактивность жителей сводит на нет этот путь сокращения перебора. Остается надеяться, что кто-то должен и выращивать хлеб, а не только митинговать. Итак, “набросок” общей логики предварительной обработки.
...
while<есть вхождения>dobegin
<исключить менее активных жителей>;
<сжать А>;
<для “карликовых” партий включить жителей, представляющих их, в состав парламента>;
<изменить значения величин, описывающих процесс формирования парламента (Res, Rt, mn, Rwork)>;
<откорректировать A>;
end;
...
Заметим, что необходимо исключить партии, “покрытые” жителями, представляющими карликовые партии из А[i].partоставшихся жителей. Это может привести к тому, что возможно появление жителей, представляющих все оставшиеся партии. Совместим проверку наличия вхождений, исключение части жителей и сжатие массива A в одной функции. Ее вид.
functionCome(var t:Nint):boolean; {Проверяем - есть ли вхождения? Если есть, то исключаем соответствующих жителей и сжимаем массив А}
vari,j,l:Nint;
begin
for i:=1 to t-1 do
for j:=i+1 to t do if A[j].part<=A[i].part then begin
A[j].part:=[];A[j].number:=0;
end;
l:=t;
for i:=1 to t do begin
if(A[i].part=[]) and (i<=l) then begin for j:=i to l-1 do A[j]:=A[j+1];
A[l].number:=0;A[l].part:=[];
Dec(l);
end;
end;
Come:=Not(t=l);
t:=l;
end;
Вариант построения процедуры исключения «карликовых» партий может быть и таким.
procedurePygmy(t:Nint;varr,p:Sset);{t - количество обрабатываемых элементов массива А; r - множество номеров жителей, включаемых в парламент; p - множество номеров партий, представляемых жителями, включенных в парламент}
vari,j:Nint;v:Sset;
begin
r:=[];p:=[];
for i:=1 to t do begin
{определяем множество партий представляемых всеми жителями кроме A[i].man}
v:=[];
for j:=1 to t do if i<>j then v:=v+A[j].part;
{если есть хотя бы одна партия, которую представляет только житель с номером A[i].man, то этого жителя мы обязаны включить в парламент}
if A[i].part*v<>A[i].Part then r:=r+[A[i].man];
end;
{формируем множество партий, имеющих представительство в данном составе парламента}
for i:=1 to t do if A[i].man in r then p:=p+A[i].part;
end;
Итак, фрагмент предварительной обработки (до перебора).
....
t:=N;Rt:=[1..N];Rwork:=[];
One(t,Rt);
while Come(t) and (Rt<>[]) do begin Rg:=[];Rp:=[];
Pygmy(t,Rg,Rp);
Rt:=Rt-Rp;Rwork:=Rwork+Rg;
ifRp<>[] then begin
for i:=1 to t do begin{исключение}
for j:=1 to N do
if (j in Rp) and (j in A[i].part) then A[i]part:=A[i].part-[j];
A[i].number:=Num(A[i].part);
end;
<сортировкаА>;
end;
end;
if (Rt<>[]) then One(t,Rt);
Блок общих отсечений. Подсчитаем для каждого значения i (1£i£t) множество партий, представляемых жителями, номера которых записаны в элементах массива с i по t (массив С:array[1..N] ofSset). Тогда, если Res - текущее решение, а Rt - множество партий, требующих представления, то при Res+C[i]£Rt решение не может быть получено и эту ветку перебора следует “отсечь”.
ФормированиемассиваС.
C[t]:=A[t].part; for i:=t-1 downto 1 do begin
C[i]:=[];C[i]:=A[i].part+C[i+1];
end;
Блок отсечений по i. Если при включении элемента с номером i в решение, значение величины Rt не изменяется, то это включение бессмысленно (A[i].part*Rt=[]).
На этом мы закончим обсуждение этой, очень интересной с методической точки зрения, задачи. Заметим, что для любой вновь возникающей идеи по сокращению перебора место для ее реализации в логике определено. А именно, предобработка, общие отсечения, покомпонентные отсечения - другого не дано.
Примечание. Графовая модель задачи (двудольный граф). Каждому жителю соответствует вершина в множестве X, каждой партии - вершина в множестве Y. Ребро (i,j)существует, если житель с номером iпредставляет партию с номером j. Требуется найти минимальное по мощности множество вершинS, такое, что SÍXи для любой вершины jÎY существует вершина iÎS, из которой выходит ребро в вершину j. Модификация задачи о нахождении минимального доминирующего множества.
2.1.7. Задача о коммивояжере (перебор вариантов)
Постановка задачи. Классическая формулировка задачи известна уже более 200 лет: имеются n городов, расстояния между которыми заданы; коммивояжеру необходимо выйти из какого-то города, посетить остальные n-1 городов точно по одному разу и вернуться в исходный город. При этом маршрут коммивояжера должен быть минимальной длины (стоимости).
Задача коммивояжера принадлежит классу NP-полных, то есть неизвестны полиномиальные алгоритмы ее решения. В задаче с n городами необходимо рассмотреть (n-1)! маршрутов, чтобы выбрать маршрут минимальной длины. Итак, при больших значениях n невозможно за разумное время получить результат.
Перебор вариантов. Оказывается, что и при простом переборе не обязательно просматривать все варианты. Это реализуется в данном классическом методе.
Структуры данных.
ConstMax=100;
Var A:array[1..Max,1..Max] ofinteger;{Матрица расстояний между городами}
B:array[1..Max,1..Max] ofbyte;{Вспомогательный массив, элементы каждой строки матрицы сортируются в порядке возрастания, но сами элементы не переставляются, а изменяются в матрице В номера столбцов матрицы А }
Way, BestWay:array[1..Max] ofbyte;{Хранится текущее решение и лучшее решение}
Nnew:array[1..Max] ofboolean;{Значение элемента массива falseговорит о том, что в соответствующем городе коммивояжер уже побывал}
BestCost:integer;{Стоимость лучшего решения}
Идея решения. Пусть мы находимся в городе с номером v. Наши действия.
Шаг 1. Если расстояние (стоимость), пройденное коммивояжером до города с номером v, не меньше стоимости найденного ранее наилучшего решения (BestCost), то следует выйти из данной ветви дерева перебора.
Шаг 2. Если рассматривается последний город маршрута (осталось только вернуться в первый город), то следует сравнить стоимость найденного нового решения со стоимостью лучшего из ранее найденных. Если результат сравнения положительный, то значения BestCostи BestWayследует изменитьи выйти из этой ветви дерева перебора.
Шаг 3. Пометить город с номером v как рассмотренный,записать этот номер по значению Countв массив Way.
Шаг 4. Рассмотреть пути коммивояжера из города v в ранее не рассмотренные города. Если такие города есть, то перейти на эту же логику с измененными значениями v, Count, Cost,иначе на следующий шаг.
Шаг 5. Пометить город v как нерассмотренный и выйти из данной ветви дерева перебора.
Пример. Ниже приведены матрицы А и В (после сортировки элементов каждой строки матрицы А).
Примечание. Можно использовать любой из методов сортировки, но авторы предпочитают использовать метод Хоара[1] из-за определенного изящества в его реализации. Рекурсивная логика плюс смена направления изменения индекса в одной циклической конструкции.
A B
| @ | |||||
| @ | |||||
| @ | |||||
| @ | |||||
| @ | |||||
| @ |
Примечание. Символом @ обозначено бесконечное расстояние.
Прежде чем перейти к обсуждению логики, целесообразно разобрать этот перебор на примере. На рисунке приведен пример и порядок просмотра городов. В кружках указаны номера городов, рядом с кружками - суммарная стоимость проезда до этого города из первого.
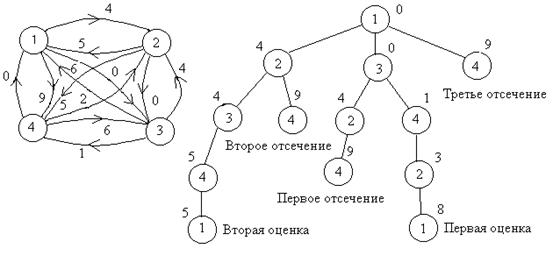
Итак, записьлогики.
procedure Solve(v,Count:byte;Cost:integer);
{v - номер текущего города;Count - счетчик числа пройденных городов; Cost - стоимость текущего решения}
vari:integer;
begin
ifCost>BestCostthenexit;{Стоимость текущего решения превышает стоимость лучшего из ранее полученных }
if Count=N then begin Cost:=Cost+A[v,1];Way[N]:=v;{Последнийгородпути. Доформировываем решение и сравниваем его с лучшим из ранее полученных.}
if Cost<BestCost then begin
BestCost:=Cost;BestWay:=Way;
end;
exit;
end;
Nnew[v]:=false;Way[Count]:=v;{Город с номером vпройден, записываем его номер в путь коммивояжера}
for i:=1 to N do if Nnew[B[v,i]] then
Solve(B[v,i], Count+1,Cost+A[v,B[v,i]]);{Поиск города, в который коммивояжер может пойти из города с номером v}
Nnew[v]:=true;{Возвращаем город с номером v в число непройденных}
end;
Первый вызов - Solve(1,1,0).
Разработка по данному «шаблону» работоспособной программы - техническая работа. Если Вы решитесь на это, то есть смысл проверить ее работоспособность на следующем примере (матрица А приведена ниже). Решение имеет вид 1 8 9 2 5 10 6 7 4 3 1, его стоимость 158.
| @ | |||||||||
| @ | |||||||||
| @ | |||||||||
| @ | |||||||||
| @ | |||||||||
| @ | |||||||||
| @ | |||||||||
| @ | |||||||||
| @ | |||||||||
| @ |
Оцените время работы программы. Если у Вас мощный компьютер, то создайте матрицу А[1..50,1..50] и попытайтесь найти наилучшее решение с помощью разобранного метода. Заметим, что набор 2500 чисел - утомительное занятие и разумная лень - «двигатель прогресса».
Задача о парламенте
На острове Новой Демократии каждый из жителей организовал партию, которую сам и возглавил. К всеобщему удивлению, даже в самой малочисленной партии оказалось не менее двух человек. К сожалению, финансовые трудности не позволили создать парламент, куда вошли бы, как предполагалось по Конституции острова, президенты всех партий.
Посовещавшись, островитяне решили, что будет достаточно, если в парламенте будет хотя бы один член каждой партии.
Помогите островитянам организовать такой, как можно более малочисленный парламент, в котором будут представлены члены всех партий.
Исходные данные: каждая партия и ее президент имеют один и тот же порядковый номер от 1 до N (4£N£150). Вам даны списки всех N партий острова Новой Демократии. Выведите предлагаемый Вами парламент в виде списка номеров ее членов. Например, для четырех партий:
| Президенты | Члены партий |
| 2,3,4 | |
| 1,4,2 | |
Список членов парламента 2 (состоит из одного члена).
Решение задачи - полный перебор всех вариантов. Покажем, что ряд эвристик позволяет сократить перебор для некоторых наборов исходных данных.
Представим информацию о партиях и их членах с помощью следующего зрительного образа - таблицы. Для примера из формулировки задачи она имеет вид:
| Президенты | Члены партий |
| 2,3,4 | |
| 1,4,2 | |
|
|
Тогда задачу можно переформулировать следующим образом. Найти минимальное число столбцов, таких, что множество единиц из них “покрывают” множество всех строк. Очевидно, что для примера это один столбец - второй. Поговорим о структурах данных.
constintNmax = 150;
enumNint {1, 2, 3, …, Nmax+1}
typedefstruct{
intpower; // мощностьмножества
int array[]; // множество
} Sste;
struct Person{
int man; // 0..Nint_1 //номержителя
intnumber; // число партий, которые он представляет
Sste part; //партии
}
struct Person A[Nint];
// Логика формирования исходных данных (фрагмент реализации)
NintNum(Sset S) // подсчитывает количество элементов в множестве
{
NintNinti, ch;
ch = 0;
for (i =0; i< N; i++)
if (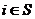
) ch++;
Num =ch;
}
voidInit()
//предполагается, что данные корректны и во входном файле они организованы
//так, как представлены в примере из формулировки задачи
{
intN;
...
scanf(“%d”, &N); // число жителей
for (i =0; i<N; i++)
{ A[i].man =i;
A[i].part=i; } // каждый житель представляет свою партию
for (i=0; i< N; i++)
{
scanf(“%d”, &t);
A[t].part:=A[t].part+ i; //житель t представляет партию с номером i, или партия с //номером i представлена жителем t
}
_getch();
}
for (i=0; i<N;i++)
A[i].number = Num(A[i].part);
....
}
Следующим очевидным шагом является сортировка массива А по значению поля number. Становится понятным и необходимость ввода поля man в структуру записи - после сортировки номер элемента массива А не соответствует номеру жителя острова.
Пока не будем задумываться о том, как сократить перебор. Попытаемся набросать общую схему.
…
voidSolve(Nintk, SsetRes,SsetRt){
// k- номер элемента массива А;
// Res - множество партий, которые представлены в текущем решении;
// Rt - множество партий, которые следует “покрыть” решением;
// min - минимальное количество членов в парламенте;
// mn - число членов парламента в текущем решении;
// Rbest - минимальный парламент;
// Rwork - текущий парламент; первый вызов - Solve(1,[],[1..N])}
Метод перебора работает только для небольших значений N, особенно, если есть ограничения (а они всегда есть) на время тестирования задачи.
Рассмотрим пример.
| Президенты | Члены партии |
| 2,3 | |
Идея. Третий житель состоит в партиях 1 и 3, второй - в 1, 2 и 3. Есть “вхождение”, третий житель менее активный, исключим его. Однако из примера проглядывает и другая идея - появилась строка, в которой только одна единица. Мы получили “карликовую” партию, ее представляет один житель, заметим, что первоначально, по условию задачи, таких партий нет. Житель, представляющий “карликовую” партию должен быть включен в решение, но он же активный и представляет еще другие партии. Значит, эти партии представлять в парламенте нет необходимости - они представлены. Исключаем эти партии (строки таблицы), но после этого возможно появление других “карликовых” партий. Рассмотрим этот процесс на следующем примере: 1 - 8,9; 2 - 10,11; 3 - 12, 13; 4 - 8,9,10; 5 - 11,12,13; 6 - 8,9,10,11; 7 - 9,10,11,12,13;8 - 1,4,6; 9 - 1,4,6,7; 10 - 2,4,6,7; 11 - 2,5,6,7; 12 - 3,5,7; 13 - 3,5,7; 14 - 8; 15 - 9; 16 - 10; 17 - 11; 18 - 12; 19 - 13.
&n
Поиск по сайту©2015-2024 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2017-12-07 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |