Тема занятия: Аксиомы статики
Воснове изучения статики твердого тела лежат аксиомы, формулировка которых предполагает, что твердое тело или материальная точка в общем случае считаются свободными, имеющими возможность совершать в рас-
сматриваемый момент времени любые перемещения в пространстве.
Аксиома инерции
Изолированная от внешних воздействий материальная точка (тело) находится в состоянии покоя или прямолинейного равномерного движения.
Аксиома равновесия двух сил
Две силы уравновешиваются, если они приложены к одному твердому телу, равны по модулю и направлены вдоль одной прямой в противопо-ложные стороны (рис. 1.2).
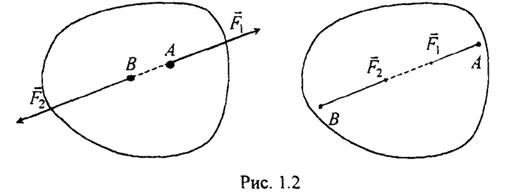
(F 1, F 2) ~ 0; F 1= - F 2
Аксиома о присоединении или исключении уравновешенной системы сил
Если к заданной системе сил присоединить или из нее исключить урав-
новешенную систему сил, то новая система сил будет эквивалентна заданной
(рис. 1.3, 1.4). (F 1, F 2, F 3, F 4) - заданная система сил.
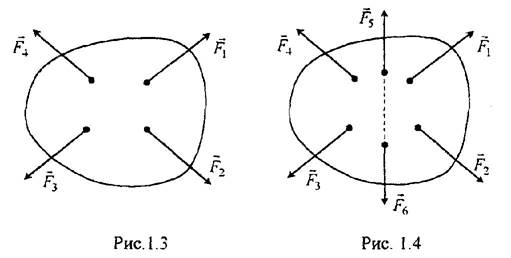
| - присоединенная система сил. | |||||||||||
| (F 5 | , F 6)~0 | ||||||||||
| (F 1 | , F 2 | , F 3 | , F 4) ~ (F 1 | , F 2 | , F 3 | , F 4 | , F 5 | , F 6). |
Следствие. Не изменяя действия на твердое тело,силу можно переноситьвдоль ей линии действия в любую другую точку тела
| Пусть на твердое тело действует сила F, | приложенная в точке А | (рис. | |||||
| 1.5). | На | линии действия этой силы возьмем | произвольную | точку | В | и | |
| приложим к ней две уравновешенные силы | F 1 | и F 2, при этом F 1 = F 2 | и | ||||
| F 2=- F. | От этого действие силы F на тело не изменится. Но силы F | и | F 2 |
также образуют уравновешенную систему, которая может быть исключена. В
результате на тело будет действовать сила F 1, равная F, но приложенная в
точке В на линии действия силы (рис. 1.6).
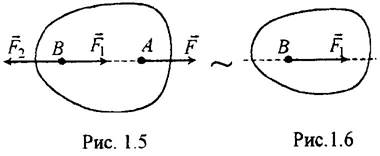
На основании этого следствия вектор силы F считается скользящим
Аксиома параллелограмма сил
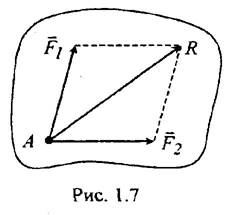
Равнодействующая двух сил, приложенных в одной точке твердого тела, приложена в той же точке, а по величине и направлению определяется диагональю параллелограмма, построенного на этих силах (рис. 1.7).
Замену двух сил одной равнодействующей называют геометрическим (или векторным) сложением этих сил,которое математически записывается так:
| R = F 1 | + F 2. | ||||||||
| Если силы F 1 и | F 2 | направлены по одной прямой в одну или противо- | |||||||
| положные стороны, то они складываются алгебраически. | |||||||||
| Модуль равнодействующей определяют по формуле | |||||||||
| Ù | |||||||||
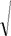 R = R =
| F 1 | + F 2 | + 2 F 1 F 2 cos(F 1 | , F 2). |
Необходимо отметить, что справедливо и обратное. Одну силу можно разложить последовательно на две, три и т.д. составляющие по заданным направлениям
Аксиома о равенстве сил действия и противодействия
Всякому действию соответствует равное и противоположно направленное противодействие.
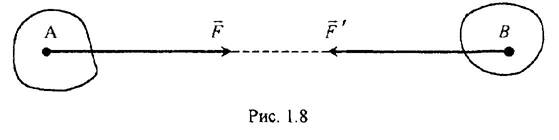
Эта аксиома утверждает, что силы взаимодействия между двумя телами (точками) равны по модулю и направлены по одной прямой в противоположные стороны (рис. 1.8).
'
Силы F и F не образуют уравновешенную
систему, так как они приложены к разным телам. Отметим, что твердые тела или материальные точки, могут взаимодействовать путем соприкосновения или посредством силовых полей, т.е. на расстоянии.
Аксиома затвердевания
Равновесие сил, приложенных к деформируемому телу, не нарушится при его затвердевании.
Эта аксиома утверждает, что условия равновесия сил, приложенных к абсолютно твердому телу, должны выполняться и для сил, приложенных к деформируемому телу.
Например, равновесие гибкой нити, на которой подвешено тело, не на-
рушится, если эта нить затвердеет.
Однако для деформируемого тела условия равновесия сил необходимы, но недостаточны. Так, например, для равновесия гибкой нити под действием двух сил, приложенных к ее концам, условия равновесия этих сил не являются достаточными, требуется еще, чтобы приложенные силы были растягивающими.
Связи. Реакции связей. Аксиома связей
Материальное тело, перемещения которого в пространстве ограничены другими телами, называется несвободным.
Связи - материальные объекты(тела),которые ограничивают перемещения данного твердого тела.
Реакция связи - сила,с которой связь действует на тело.
Активные - силы,которые не являются реакциями связей.
Упомянутые ранее внешние и внутренние силы могут быть активными и реакциями связей.
Аксиома связей
Всякое несвободное тело можно рассматривать как свободное, если связи условно отбросить и заменить их действие реакциями связей.
Реакции связей зависят от приложенных к телу активных сил и от вида связей. Поэтому очень важно уметь правильно заменять действие отбро-шенных связей их реакциями. При этом надо помнить, что реакция связи направлена в сторону, противоположную той, в которую связь препятствует перемещению тела. Если связь препятствует перемещению тела по не-скольким направлениям, направление реакции связи неизвестно, ее обычно раскладывают по правилу параллелограмма на составляющие, направленные параллельно осям координат.
Домашнее задание:
1. Прочитайте конспект
2. Выпишите аксиомы и сделайте к ним рисунки