Поверка амперметра
Для поверки амперметра необходимо:
1. Собрать цепь по схеме (рисунок 1.5), используя приборы и элементы лабораторного стенда.
Рисунок 1.5 — Схема поверки амперметра
На рисунке 1.5 РАx — поверяемый амперметр (по указанию преподавателя); РА0 — образцовый прибор (прибор, который необходимо подобрать); R — резистор; TV — лабораторный автотрансформатор (ЛАТр); QF — авто-матический выключатель;
2. Убедиться, что движок ЛАТра установлен в положение, соответствующее минимальному значению напряжения на выходе, подать напряжение на цепь;
3. Меняя напряжение, подаваемое на электрическую цепь с помощью ЛАТра, произвести поверку амперметра на всех оцифрованных точках его шкалы (0; 0,2; 0,4; 0,6; 0,8; 1,0 А) при возрастании и убывании измеряемой величины;
4. Результаты измерений и вычислений занести в таблицу 1.1.
В таблице I 0, I 0¯— показания образцового прибора при изменении питающего напряжения вверх и вниз соответственно; I 0ср — среднее значение показания образцового прибора
;
Таблица 1.1
| № п/п | Измерено | Вычислено | |||||||
| Ix, A | I 0, A | I 0¯, A | I 0ср, A | D I, А | D Р, А | d ,% | g ,% | ||
| 1. | |||||||||
| 2. | 0,2 | ||||||||
| 3. | 0,4 | ||||||||
| 4. | 0,6 | ||||||||
| 5. | 0,8 | ||||||||
| 6. | 1,0 | ||||||||
5. По результатам измерений определить погрешности поверяемого амперметра и дать заключение о его классе точности.
Поверка вольтметра
1. Собрать схему согласно рисунку 1.6 на лабораторном стенде.
Рисунок 1.6 — Схема поверки вольтметра
На рисунке 1.6 РVx — поверяемый вольтметр; РV 0 — образцовый вольтметр, который необходимо подобрать.
|
|
2. Убедиться, что движок ЛАТра установлен в положение, соответствующее минимальному значению напряжения на выходе, подать напряжение на цепь.
3. Меняя напряжение, подаваемое на электрическую цепь с помощью ЛАТра, произвести поверку вольтметра на всех оцифрованных точках его шкалы при возрастании и убывании измеряемой величины.
4. Результаты измерений и вычислений занести в таблицу 1.2.
Таблица 1.2
| № п/п | Измерено | Вычислено | ||||||
| Ux, В | U 0,В | U 0¯,В | U 0ср, В | D U, В | D Р, В | d ,% | g ,% | |
| 1. | ||||||||
| 2. | ||||||||
| 3. | ||||||||
| 4. | ||||||||
| 5. | ||||||||
| 6. |
В таблице U 0, U 0¯— показания образцового прибора при изменении питающего напряжения вверх и вниз соответственно; U 0ср — среднее значение показания образцового вольтметра.
5. По результатам измерений определить погрешности поверяемого вольтметра и сделать вывод о его соответствии своему классу точности.
Содержание отчета
1. Название и цель работы.
2. Конспективная запись изученного теоретического материала в соответствии с программой работы.
3. Схемы исследований и таблицы экспериментальных и расчетных данных.
4. Выводы о соответствии поверяемых приборов заявленным классам точности.
ЛАБОРАТОРНАЯ РАБОТА № 2
ИССЛЕДОВАНИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
С ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ
КАТУШКИ ИНДУКТИВНОСТИ И КОНДЕНСАТОРА.
|
|
РЕЗОНАНС НАПРЯЖЕНИЙ
Цель работы: Изучить и экспериментально проверить основные свойства электрической цепи переменного тока с нагрузкой в виде последовательного соединения активного, индуктивного и ёмкостного сопротивлений. Исследовать резонанс напряжений.
Подготовка к работе
1. Изучить тему «Цепь переменного тока с последовательным соединением активного, индуктивного и ёмкостного сопротивлений» по конспекту лекций и по литературе [1, § 1.5–1.7, 1.9; 3, § 2.6–2.9, 2.11, 2.21].
2. Ознакомиться с описанием работы по методическим указаниям.
3. Самоконтроль:
1) Какие реальные электротехнические элементы обладают индуктивным, ёмкостным, активным сопротивлением?
2) Как влияет изменение частоты питающего напряжения на величину активного, индуктивного и ёмкостного сопротивлений?
3) Закон Ома для цепи переменного тока с последовательным соединением активного, индуктивного и ёмкостного сопротивлений;
4) Что представляет собой треугольник напряжений и треугольник сопротивлений для цепи переменного тока с последовательным соединением активного, индуктивного и ёмкостного сопротивлений?
5) Условия возникновения и признаки резонанса напряжений;
6) Векторная диаграмма тока и напряжений в цепи с последовательным соединением активного, индуктивного и ёмкостного сопротивлений;
7) Какое практическое значение имеет резонанс напряжений для слаботочных и сильноточных цепей?
4. Подготовить протокол отчета.
Сведения из теории
Схема электрической цепи с последовательным соединением активного, индуктивного и ёмкостного сопротивлений представлена на рисунке 2.1, на котором R — активное сопротивление; L — индуктивность катушки индуктивности; С — ёмкость конденсатора; UR, UL, UC — падения напряжений на активном, индуктивном и ёмкостном сопротивлениях; U — напряжение питания на зажимах цепи; I — ток в цепи.
|
|
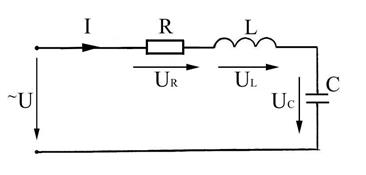
Рисунок 2.1 — Последовательное соединение элементов R, L и С
В соответствии с законом Ома, связь между током и напряжением для действующих значений можно представить выражением:
,
где 
— полное сопротивление цепи; R, XL, XC — соответственно активная, индуктивная и ёмкостная составляющие полного сопротивления цепи.
В комплексной форме закон Ома можно представить выражением:
,
где 
— комплекс действующего значения напряжения на входе цепи; 
— комплекс полного сопротивления цепи.
Индуктивное и ёмкостное сопротивления цепи зависят не только от физических параметров катушки и конденсатора, а также и от частоты питающего напряжения f.
Эта зависимость определяется выражениями:
ХL = w L = 2 p fL, XC = 
.
Приложенное к рассматриваемой электрической цепи питающее напряжение U уравновешивается падением напряжения на отдельных ее участках.
Согласно второму закону Кирхгофа, этому положению соответствует равенство:
,
где 
— векторы действующих значений приложенного к цепи напряжения на активном, индуктивном и ёмкостном элементах соответственно.
Следует обратить внимание, что законы Кирхгофа записываются в комплексной или векторной форме, т. е. 2-ой закон Кирхгофа можно записать в виде:
.
Векторная диаграмма для рассматриваемой цепи, из которой можно выделить треугольник напряжений аbс представлена на рисунке 2.2.
Гипотенуза треугольника напряжений соответствует действующему значению приложенного к цепи напряжения U, а катеты — активной и реактивной составляющим этого напряжения.
Рисунок 2.2 —Треугольник напряжений
Угол между векторами напряжения и тока j называется углом сдвига фаз и определяется разностью начальных фаз напряжения и тока, т. е. j = y u - y i.
Разделив величины длин сторон треугольника напряжений на число, равное действующему значению тока в рассматриваемой цепи, получим треугольник, у которого стороны будут в масштабе соответствовать значениям сопротивлений этой цепи. Этот треугольник называется треугольником сопротивлений (рисунок 2.3.).
Рисунок 2.3 — Треугольник сопротивлений
Гипотенуза треугольника сопротивлений соответствует в масштабе полному сопротивлению цепи Z, а катеты — его активной R и реактивной Х составляющим.
Значение j зависит от соотношения активного и реактивного сопротивлений цепи. Из треугольника сопротивлений угол сдвига фаз можно определить как
.
В зависимости от соотношения Х и R могут иметь место три характерных режима работы цепи:
1) активно-индуктивный, когда ХL>XC, j > 0 (рисунок 2.4);
2) активно-ёмкостной, при котором ХL<XC, j <0 (рисунок 2.6);
3) активный, при котором ХL=XC, j = 0, т. е. ток и напряжение совпадают по фазе (рисунок 2.5).
Рисунок 2.4 Рисунок 2.5 Рисунок 2.6
Режим отставания по фазе тока от напряжения имеет место при положительных Up, когда индуктивная составляющая напряжения больше активной составляющей: UL>UC. Последнее обеспечивается, если ХL>XC.
Режим, при котором ток опережает по фазе приложенное напряжение, имеет место при условии UL<UC и, соответственно, при ХL<XC.
При ХL=XC, также UL=UC, и при этом также возможен резонанс напря-жений, основным проявлением которого можно назвать резкое увеличение величин напряжения на реактивных элементах цепи (усиление по напряже-нию).