Цель работы: Исследовать трехфазную цепь с нагрузкой, соединенной по схеме «звезда» с нейтральным и без нейтрального провода.
Подготовка к работе
1. Изучить тему «Трехфазные цепи» по литературе [1, § 2.1, 2.2, 2.4; 3, § 3.1, 3.2, 3.4] и по конспекту лекций.
2. Ознакомиться с описанием лабораторной работы.
3. Самоконтроль:
1) Что называется трехфазной цепью синусоидального тока?
2) Схемы, основные соотношения, достоинства и недостатки при соединении потребителей (приёмников) в трехфазных цепях по схеме «звезда» с нейтральным проводом и без нейтрального провода?
3) Симметричная и несимметричная нагрузка в трехфазных цепях;
4) Назначение нейтрального провода. Как можно определить ток в нейтраль-ном проводе?
5) Как связаны линейные токи и напряжения с их фазными значениями в трехфазной цепи при соединении приемников по схеме «звезда»?
6) Активная, реактивная и полная мощности в трехфазных цепях синусоидального тока.
4. Подготовить протокол отчета.
Сведения из теории
Трехфазной цепью синусоидального тока называют совокупность трех однофазных цепей, в каждой из которых действуют синусоидальные ЭДС одинаковой амплитуды и частоты, но имеющие сдвиг по фазе относительно друг друга на угол 120º.
Источником электрической энергии в трехфазной цепи является синхронный генератор, имеющий три одинаковые обмотки (фазы), сдвинутые в пространстве на угол 120º, расположенные на статоре. Начала обмоток фаз обозначают А, В, С, концы — Х, Y, Z соответственно. При вращении ротора, который представляет собой электромагнит постоянного тока, в обмотках статора будут индуцироваться переменные ЭДС, сдвинутые относительно друг друга по фазе на 120º (2p/3).
еА = Еm sinw t,
еB = Еm sin ( w t - 2p/3 ),
еC = Еm sin ( w t + 2p/3 ),
где Еm — амплитудное значение ЭДС фаз генератора.
Если ЭДС трех фаз равны по амплитуде и сдвинуты по фазе на угол 120°, то такую систему называют симметричной трехфазной системой. Для нее характерно, что мгновенные значения ЭДС в определенный момент времени
еА + еВ+ еC = 0.
Для источников и приемников трехфазной цепи существуют две схемы соединений: звездой и треугольником.
При соединении генератора звездой концы обмоток генератора объединяют в общую точку, называемую нейтральной, обозначают ее буквой N (рисунок 4.1).
При соединении трехфазного потребителя звездой концы фаз потребителя объединяют в общую точку, называемую нейтральной точкой нагрузки, и обозначают n (рисунок 4.1).
Начала фаз потребителя и генератора объединяют проводами, называемыми линейными. Провод, соединяющий нейтральные точки генератора и потребителя, называют нейтральным. Полученную схему (рисунок 4.1) называют «звезда»–«звезда» с нейтральным проводом (четырехпроводная трехфазная).
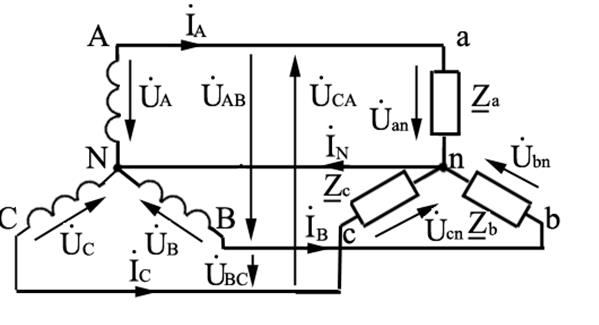
Рисунок 4.1 — Схема трехфазной цепи «звезда»–«звезда» с нейтральным проводом
Токи, протекающие по линейным проводам, называют линейными токами и обозначают IA, IB, IC или I л. За положительное направление условно принимают направление от генератора к нагрузке.
Ток, протекающий по нейтральному проводу, обозначают IN. Его положительное направление принято от нагрузки к генератору (от точки N к точке n).
Напряжение между линейными проводами (между началом фаз) называют линейным, обозначают при помощи двух индексов: 
(рисунок 4.1).
Напряжение между нейтральной точкой и концом фазы называют фазным. Обозначают фазное напряжение генератора — 
, фазное напряжение потребителя — 
. 
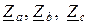обозначили всю совокупность комплексного сопротивления потребителей, включенных в каждую фазу. Потребители определяют фазные токи 
. Из схемы (рисунок 4.1) видно, что при соединении потребителя по схеме звезда линейные токи равны фазным токам, т. е. I л = I ф.
Согласно первому закону Кирхгофа, 
.
Сопротивления линейных проводов и нейтрального провода малы и ими можно пренебречь. Тогда линейные напряжения генератора примерно равны линейным напряжениям потребителей.
Согласно второму закону Кирхгофа,
,
т. е. линейное напряжение равно векторной разности соответствующих фазных напряжений.
Для симметричного источника векторная диаграмма напряжений имеет вид как на рисунке 4.2, а.
Из векторной диаграммы следует, что U л = 
U ф.
При анализе режима работы трехфазной цепи исходим из того, что трехфазный источник является симметричным. Следовательно, при принятом предположении о сопротивлениях линейных и нейтрального проводов, система фазных напряжений потребителя при соединении «звезда» с нейтральным проводом симметрична, поэтому
.
С учетом сказанного векторная диаграмма напряжений приёмника будет иметь такой же вид (рисунок 4.2, б), т. е. точки нейтрали генератора и приемника совпадут и напряжение между нейтралями генератора и потребителя UnN= 0.
а) б)
Рисунок 4.2 — Векторные диаграммы:
а — напряжений генератора; б — напряжений и токов потребителя
Фазные токи зависят от суммарного сопротивления всех потребителей данной фазы. По направлению они могут совпадать со своим напряжением (нагрузка чисто активная), опережать свое напряжение (нагрузка активно-ёмкостная) и отставать от своего напряжения (нагрузка активно-индуктивная). Векторная сумма фазных токов равна току нейтрального провода IN (рисунок 4.2).
Таким образом, нейтральный провод обеспечивает независимую работу потребителей в разных фазах. Например, потребители в одной из фаз можно выключить (обрыв фазы) или сделать короткое замыкание (аварийный режим), в других двух фазах напряжение останется номинальное, т. е. то, которое и было, то, на которое рассчитан потребитель.
Нагрузка, при которой все комплексные сопротивления фаз равны между собой: 
, — называется симметричной.
При симметричной нагрузке фазные токи тоже должны быть равны между собой и сдвинуты относительно друг друга по фазе на 120º. В связи с этим векторная сумма токов должна быть равна нулю, и необходимость нейтрального провода отпадает.
Следует особо обратить внимание на то, что в случае отключения или выхода из строя нейтрального провода при несимметричной нагрузке фазные напряжения оказываются неравными друг другу, происходит так называемый «перекос фаз».
Причина в следующем: в трехпроводной трехфазной цепи при любом режиме нагрузки векторная сумма фазных токов равна нулю, т. е.
.
При изменении сопротивления хотя бы в одной из фаз изменится величина соответствующего тока. А это приведет к изменению и остальных фазных токов согласно первому закону Кирхгофа. Но так как сопротивления в других фазах не изменялись, то согласно закону Ома (U = IZ) изменяются и напряжения, т. е. фазные напряжения на потребителе станут разными, отличными от номинальных. Между нейтральными точками генератора и потребителя появляется напряжение, называемое напряжением смещения нейтрали (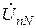
).
На основании второго закона Кирхгофа фазные напряжения на потребителе будут равны векторной разности соответствующих фазных напряжений генератора и напряжения смещения нейтрали, т. е.
; 
; 
.
Векторная диаграмма для случая несимметричной нагрузки при соединении потребителя по схеме «звезда» без нейтрального провода представлена на рисунке 4.3.
В связи с вышеизложенным соединение потребителей по схеме «звезда» без нейтрального провода используется лишь в том случае, если трехфазная нагрузка симметричная.
Рисунок 4.3 — Векторная диаграмма напряжений несимметричного режима работы цепи при соединении нагрузок звездой
Мощности трехфазного потребителя в общем случае можно определить как сумму мощностей всех фаз. При соединении приёмников звездой активная, реактивная и полная мощности определяются по формулам:
,
,
.
При симметричной нагрузке эти формулы упрощаются и записываются следующим образом:
,
,
.
Непосредственно измерить активную мощность трехфазной нагрузки можно с помощью трех ваттметров, включенных в каждую фазу (метод трех ваттметров) или с помощью двух ваттметров, включенных по току в две фазы и использующих линейное напряжение.