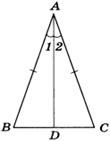
Дано: ∆АВС, АВ = АС.
Доказать, что ∠В = ∠С.
Доказательство: В ∆АВС из вершины А проведем биссектрису АД. Треугольники ABD и ACD равны по первому признаку равенства треугольников (АВ = АС по условию, AD – общая сторона, ∠1 = ∠2, так как AD — биссектриса). Из равенства этих треугольников следует, что ∠В = ∠С. Ч.т.д.
 3. Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 2100. Найдите все углы. Решение:
3. Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 2100. Найдите все углы. Решение:
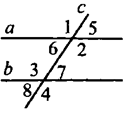

 2. (п.19) Если сторона и 2 прилежащих к ней угла одного треугольника соответственно равны стороне и 2 прилежащим к ней углам другого треугольника, то такие треугольники равны.
Дано: ∆АВС и ∆А1В1С1, у них АВ=А1В1, ∠А = ∠А1, ∠В = ∠В1
Доказать, что ∆АВС = ∆А1В1С1
Доказательство: Наложим ∆АВС на ∆А1В1С1 так, чтобы сторона АВ совпала со стороной А1В1 (по условию они равны, значит совпадут). Так как по условию ∠А = ∠А1 и ∠В = ∠В1, то сторона АС наложится на луч А1С1, а сторона ВС на луч В1С1. Вершина С окажется лежащей как на луче А1С1, так и на луче В1С1, а значит совпадет с вершиной С1. Все три точки у треугольников совпали, значит они равны. Ч.т.д.
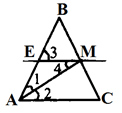
3.АМ – биссектриса ∆АВС. Через точку М проведена прямая, параллельная АС и пересекающая сторону АВ в точке Е. Докажите, что ∆АМЕ равнобедренный.
Доказательство:АС || ЕМ, значит ∠1 = ∠3 (как соответственные углы), ∠2 = ∠4 (как накрест лежащие углы), ∠1 = ∠2 (т.к. АМ – биссектриса).
Следовательно ∠1 = ∠4, а это углы при основании в ∆АМЕ, значит этот треугольник равнобедренный и АЕ = ЕМ. Ч.т.д.
2. (п.19) Если сторона и 2 прилежащих к ней угла одного треугольника соответственно равны стороне и 2 прилежащим к ней углам другого треугольника, то такие треугольники равны.
Дано: ∆АВС и ∆А1В1С1, у них АВ=А1В1, ∠А = ∠А1, ∠В = ∠В1
Доказать, что ∆АВС = ∆А1В1С1
Доказательство: Наложим ∆АВС на ∆А1В1С1 так, чтобы сторона АВ совпала со стороной А1В1 (по условию они равны, значит совпадут). Так как по условию ∠А = ∠А1 и ∠В = ∠В1, то сторона АС наложится на луч А1С1, а сторона ВС на луч В1С1. Вершина С окажется лежащей как на луче А1С1, так и на луче В1С1, а значит совпадет с вершиной С1. Все три точки у треугольников совпали, значит они равны. Ч.т.д.
3.АМ – биссектриса ∆АВС. Через точку М проведена прямая, параллельная АС и пересекающая сторону АВ в точке Е. Докажите, что ∆АМЕ равнобедренный.
Доказательство:АС || ЕМ, значит ∠1 = ∠3 (как соответственные углы), ∠2 = ∠4 (как накрест лежащие углы), ∠1 = ∠2 (т.к. АМ – биссектриса).
Следовательно ∠1 = ∠4, а это углы при основании в ∆АМЕ, значит этот треугольник равнобедренный и АЕ = ЕМ. Ч.т.д.

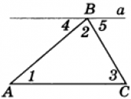 Углы 1 и 4 являются накрест лежащими углами при пересечении параллельных прямых а и АС секущей АВ, а углы 3 и 5 – накрест лежащими углами при пересечении тех же параллельных прямых секущей ВС.
Поэтому ∠4 = ∠1 = ∠А, ∠5 = ∠3 = ∠С. Отсюда, учитывая равенство (*), получаем: ∠l + ∠2 + ∠3 = 180°, или ∠A + ∠B + ∠C = 180°. Ч.т.д.
Углы 1 и 4 являются накрест лежащими углами при пересечении параллельных прямых а и АС секущей АВ, а углы 3 и 5 – накрест лежащими углами при пересечении тех же параллельных прямых секущей ВС.
Поэтому ∠4 = ∠1 = ∠А, ∠5 = ∠3 = ∠С. Отсюда, учитывая равенство (*), получаем: ∠l + ∠2 + ∠3 = 180°, или ∠A + ∠B + ∠C = 180°. Ч.т.д.
 3. На биссектрисе угла А взята точка Е, а на сторонах этого угла точки В и С так, что ∠АЕС = ∠АЕВ. Докажите, что ВЕ = СЕ.
Доказательство:Рассмотрим ∆АСЕ и ∆АВЕ.
У них: ∠ВАЕ=∠САЕ, т.к. АЕ – биссектриса угла А,
∠АЕС = ∠АЕВ (по условию). Сторона АЕ – общая.
Значит ∆АСЕ = ∆АВЕ по II признаку. Тогда ВЕ = СЕ.Ч.т.д.
3. На биссектрисе угла А взята точка Е, а на сторонах этого угла точки В и С так, что ∠АЕС = ∠АЕВ. Докажите, что ВЕ = СЕ.
Доказательство:Рассмотрим ∆АСЕ и ∆АВЕ.
У них: ∠ВАЕ=∠САЕ, т.к. АЕ – биссектриса угла А,
∠АЕС = ∠АЕВ (по условию). Сторона АЕ – общая.
Значит ∆АСЕ = ∆АВЕ по II признаку. Тогда ВЕ = СЕ.Ч.т.д.