Цель работы. Исследовать электрическую цепь трехфазного переменного тока, содержащую приемник электрической энергии, соединенный по схеме «звезда» с нулевым (нейтральным) проводом и без него.
Краткие теоретические сведения
Трехфазная симметричная система ЭДС состоит из трех ЭДС, одинаковых по амплитуде и частоте, но сдвинутых друг относительно друга на 120º.
При соединении «звездой» концы обмоток фаз генератора X, Y, Z соединяют в одну общую точку N, называемую нейтральной или нулевой. К началам фаз генератора А, В, С подключают провода, с помощью которых источник питания (генератор) соединяется с приемником. Эти провода называются линейными, а трехфазная система – трехпроводной (рис.20).
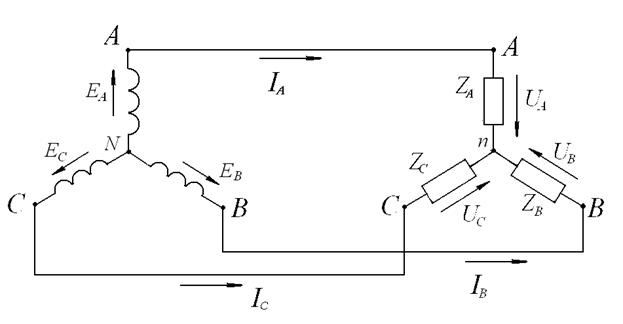
Рис.20. Трехпроводная система трехфазного переменного тока (соединение по схеме «звезда»).
Если нейтральная (нулевая) точка N генератора соединена проводом с нейтральной (нулевой) точкой n приемника, то система называется четырехпроводной с нулевым (нейтральным) проводом (рис.19).
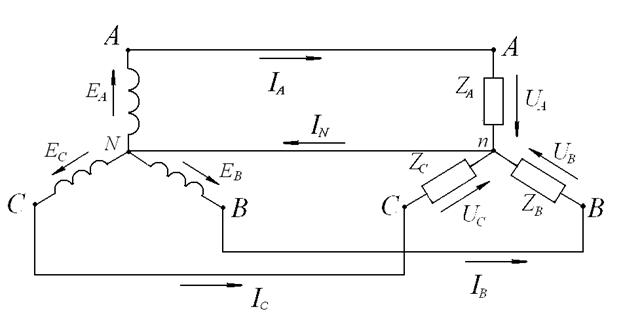
Рис.21. Четырехпроводная система трехфазного переменного тока с нулевым (нейтральным) проводом (соединение по схеме «звезда»).
При соединении «звездой» каждая фаза генератора, линейный провод и фаза нагрузки соединены между собой последовательно и через них проходит один и тот же ток. Следовательно, при соединении «звездой» линейный ток равен фазному, т.е.
I Л = I Ф. (36)
Напряжения между началом и концом каждой фазы нагрузки  А,
А,  В,
В,  С, равные (при пренебрежении падением напряжения в проводах) напряжениям на фазах генератора, называются фазными напряжениями. Напряжения между линейными проводами
С, равные (при пренебрежении падением напряжения в проводах) напряжениям на фазах генератора, называются фазными напряжениями. Напряжения между линейными проводами  AB,
AB,  BC,
BC,  CA называются линейными напряжениями. Токи, протекающие в фазах нагрузки
CA называются линейными напряжениями. Токи, протекающие в фазах нагрузки  A,
A,  B,
B,  C, называются фазными токами. Для системы «звезда» линейные токи одни и те же с фазными
C, называются фазными токами. Для системы «звезда» линейные токи одни и те же с фазными  Л =
Л =  Ф.
Ф.
По второму закону Кирхгофа можно определить соотношения между фазными и линейными напряжениями
 AB =
AB =  A −
A −  B
B
 BC =
BC =  B −
B −  C (37)
C (37)
 CA =
CA =  C −
C −  A
A
Так как трехфазная система генератора симметрична, то действующие значения ЭДС генератора равны между собой и равны действующим значениям на нагрузке при пренебрежении падением напряжения в линии 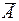 A =
A = 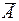 B =
B = 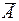 C =
C =  A =
A =  B =
B =  C =
C =  Ф.
Ф.
ЕA = ЕB = ЕC = UA = U B = U C = U Ф.
Исходя из равенства угла сдвига между фазами 120 на генераторе и нагрузке и выведенных из второго закона Кирхгофа уравнений (37), равны между собой и действующие значения линейных напряжений
UAB = UBC = UCA = UЛ .
Векторная диаграмма фазных и линейных напряжений (рис.20) будет для симметричного генератора и четырехпроводной системы «звезда» неизменна при любой нагрузке. На рис.20а приведена полярная, а на рис. 20б – топографичекая векторная диаграмма.

| 
|
| а) | б) |
Рис.22. Полярная и топографическая векторные диаграммы напряжений в четырехпроводной системе «звезда»
Из векторной диаграммы (рис.20а) получим соотношение между линейными и фазными напряжениями.
UAB = 2 UА ∙ cos 30º = 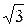 UА =
UА = 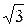 UФ.
UФ.
В общем случае для четырехпроводной системы «звезда» при любой нагрузке
UЛ = 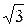 UФ . (38)
UФ . (38)
К симметричному трехфазному генератору с нейтральным проводом может быть присоединена любая симметричная и несимметричная нагрузка. Нагрузка называется симметричной, если сопротивления и углы сдвига фаз между напряжением и током всех ее фаз одинаковы
ZA = ZB = ZC, φA = φB = φC. (39)
Несоблюдение любого из условий (39) приведет к нарушению симметричности нагрузки трехфазной системы.
Рассмотрим четырехпроводную трехфазную систему с нагрузкой, соединенной по схеме «звезда».
1) Симметричная активная нагрузка: ZA = ZB = ZC = RA = RB = RC
IA = 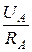
IB = 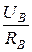
IC = 
Так как UA = UB = UC = UФ = 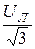 , то
, то
IA = IB = IC = IФ = 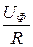 =
= 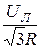 (40)
(40)
Топографическая векторная диаграмма токов и напряжений при симметричной активной нагрузке представлена на рис.21.

Рис.23. Топографическая векторная диаграмма четырехпроводной трехфазной системы «звезда» при симметричной активной нагрузке
По первому закону Кирхгофа
 A +
A +  B +
B +  C =
C =  N.
N.
Для симметричной нагрузки
 N = 0.
N = 0.
2) Несимметричная активная нагрузка: ZA = RA; ZB = RB; ZC = RC; RA ≠ RB ≠ RC; IA ≠ IB ≠ IC
 A =
A = 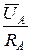 IA =
IA = 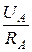 =
= 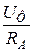 =
= 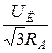 ;
;
 B =
B = 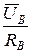 IB =
IB = 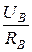 =
=  =
= 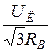 ; (41)
; (41)
 C =
C = 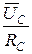 IC =
IC =  =
= 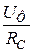 =
=  ;
;
 N =
N =  A +
A +  B +
B +  C . (42)
C . (42)
Топографическая векторная диаграмма токов и напряжений при несимметричной нагрузке представлена на рис.22

Рис.24. Топографическая векторная диаграмма четырехпроводной трехфазной системы «звезда» при несимметричной активной нагрузке
Для нахождения значения тока IN по выражению (42) необходимо найти геометрическую сумму векторов  A,
A,  B и
B и  C (рис.22). В результате получаем
C (рис.22). В результате получаем
IN =  (43)
(43)
Общая мощность трехфазной цепи в этом случае будет равна
P = 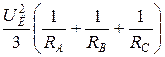 (44)
(44)
Трехпроводная трехфазная система с соединением нагрузки по схеме «звезда» без нулевого (нейтрального) провода (рис.20).
Рассмотрим, что произойдет с токами и напряжениями при отключении нейтрального провода (рис.20).
В трехпроводной системе, соединенной по схеме «звезда» между нулевой точкой нагрузки и нулевой точкой генератора возникает напряжение UnN, величина и направление которого зависят от величины и характера нагрузки.
Согласно методу двух узлов в случае активной нагрузки напряжение UnN, можно выразить следующим образом
 nN =
nN = 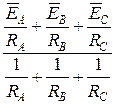 . (45)
. (45)
Составим уравнения по второму закону Кирхгофа
 nN =
nN = 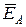 −
− 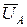
 nN =
nN =  −
− 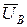 (46)
(46)
 nN =
nN = 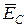 −
− 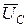
Откуда
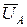 =
= 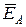 −
−  nN
nN
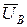 =
=  −
−  nN (47)
nN (47)
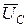 =
= 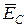 −
−  nN.
nN.
Токи в фазах нагрузки определяются
 A =
A =  =
= 
 B =
B =  =
= 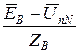 (48)
(48)
 C =
C = 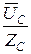 =
= 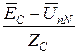
Проанализируем электрическое состояние трехпроводной трехфазной системы, соединенной по схеме «звезда», при различных значениях нагрузки.
1) Симметричная активная нагрузка: ZA = ZB = ZC = RA = RB = RC
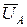 =
= 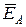
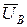 =
= 
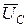 =
= 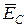
 nN = 0
nN = 0
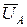 =
= 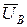 =
= 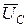
 A =
A = 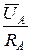 IA =
IA = 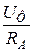
 B =
B = 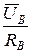 IB =
IB = 
 C =
C =  IC =
IC = 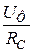
 A +
A +  B +
B +  C =
C =  N = 0
N = 0
 A =
A =  B =
B =  C =
C =  Ф.
Ф.
Векторная диаграмма токов и напряжений приведена на рис.25.

Рис.25. Топографическая векторная диаграмма трехпроводной трехфазной системы «звезда» при симметричной активной нагрузке
Векторная диаграмма аналогична диаграмме, построенной для четырехпроводной системы с симметричной активной нагрузкой. Подобным образом аналогична диаграмма для симметричной активно-реактивной нагрузки, поэтому при симметричной нагрузке отпадает необходимость нулевого провода, т.к. ток в нем равен нулю.
2) Несимметричная активная нагрузка: ZA = RA; ZB = RB; ZC = RC; RA ≠ RB ≠ RC; IA ≠ IB ≠ IC
При отключении нейтрального провода ток I 0 становится равным нулю, следовательно, при несимметричной нагрузке должны измениться и токи IA, IB, IC. изменение же этих токов может произойти только при условии, что изменились напряжения на фазах нагрузки. Следовательно, фазные напряжения нагрузки теперь не будут представлять симметричную систему векторов, т.к. действующие значения этих напряжений не будут равны между собой, а их фазовый сдвиг относительно друг друга будет отличаться от 120º (рис.26).

Рис.26. Топографическая векторная диаграмма трехпроводной трехфазной системы «звезда» при несимметричной активной нагрузке
Нулевая точка нагрузки n смещена относительно нулевой точки генератора N.
Из рис.25 видно, что напряжения на фазах нагрузки определяются как
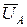 =
= 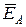 −
−  nN
nN
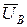 =
=  −
−  nN
nN
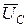 =
= 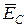 −
−  nN.
nN.
что соответствует выражению (47)
Проведя геометрическое сложение векторов 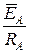 ,
, 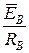 ,
,  и разделив полученный результат на значение проводимости Y =
и разделив полученный результат на значение проводимости Y = 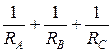 , в соответствии с выражением (45), получаем вектор
, в соответствии с выражением (45), получаем вектор  nN.
nN.
Вычитая полученный результат из векторов 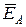 ,
,  , и
, и 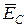 , находим соответственно
, находим соответственно 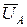 ,
, 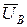 и
и 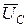 .
.
В результате получаем выражения для расчета действующих значений фазных напряжений U A, U В, U С и токов I A, I В, I С.
U А = U Л ∙  ; I A =
; I A = 
U В = U Л ∙ 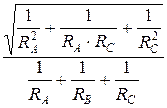 ; I В =
; I В = 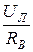
U С = U Л ∙ 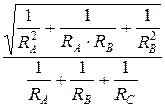 ; I С =
; I С =  (49)
(49)
Для измерения мощности в работе используется метод двух ваттметров W 1 и W 2 (рис.27).
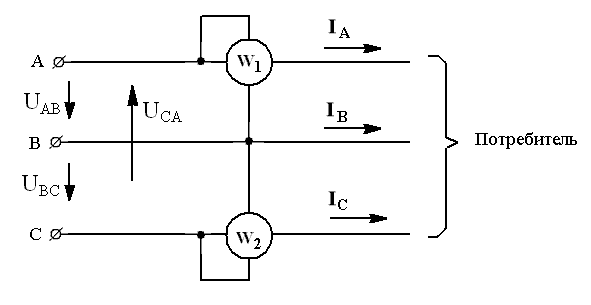
Рис.27. Схема измерения мощности методом двух ваттметров
Поясним принцип работы этого метода.
Приборы для измерения активной мощности (ваттметры), включенные в цепь однофазного переменного тока, измеряют величину
Р = U ∙ I ∙ cos (U ^ I), (50)
где U - напряжение, приложенное к обмотке напряжения ваттметра;
I - ток, протекающий по токовой обмотке ваттметра;
U ^ I = φ - угол сдвига между напряжением и током.
Активная мощность трехфазной цепи при симметричной нагрузке фаз может быть выражена двумя равноценными формулами
Р = 3∙ U Ф ∙ I Ф ∙ cos φ или
Р = 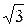 ∙ U Л ∙ I Ф ∙ cos φ. (51)
∙ U Л ∙ I Ф ∙ cos φ. (51)
Для измерения активной мощности в трехпроводных цепях трехфазного тока как при симметричной, так и при несимметричной нагрузке фаз (независимо от способа соединения нагрузки «звездой» или «треугольником»), широкое практическое применение получил метод двух ваттметров, включенных как показано на рис.14.
Показания ваттметров W 1 и W 2 можно записать следующим образом
Р 1 = U АВ ∙ I A ∙ cos (U AB ^ I A)
Р 2 = U СВ ∙ I C ∙ cos (U CB ^ I C) (52)
Обозначим через α и β соответственно углы (U AB ^ I A) и (U CB ^ I C). Для определения α и β построим векторную диаграмму для случая симметричной активно-индуктивной нагрузки (рис.27). Согласно построению α = 30º + φ, β = 30º – φ.
Учитывая, что при симметричной нагрузке U АВ = U СВ = U Л и I А = I С = I Л, показания ваттметров можно записать следующим образом:
Р = Р 1 + Р 2 = U Л ∙ I Л ∙ [cos (30º + φ) + cos (30º – φ)] = 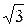 U Л ∙ I Л ∙ cos φ. (53)
U Л ∙ I Л ∙ cos φ. (53)
Полученное выражение совпадает с выражением (45). Таким образом доказано, что сумма показаний двух ваттметров будет равна активной мощности трехфазной цепи.

Рис.28. Векторная диаграмма трехпроводной системы трехфазного переменного тока с симметричной активно-индуктивной нагрузкой
Разность показаний двух ваттметров, умноженная на 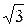 , будет равна реактивной мощности цепи Q.
, будет равна реактивной мощности цепи Q.
Q = 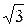 (Р 1 – Р 2) =
(Р 1 – Р 2) = 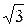 U Л ∙ I Л ∙ [cos (30º + φ) – cos (30º – φ)] =
U Л ∙ I Л ∙ [cos (30º + φ) – cos (30º – φ)] = 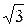 U Л ∙ I Л ∙sin φ. (54)
U Л ∙ I Л ∙sin φ. (54)
Показания каждого из ваттметров в отдельности не имеют никакого физического смысла, за исключением случая симметричной и чисто активной нагрузки, при которой Р 1 = Р 2 и составляет половину измеряемой мощности трехфазной цепи.
ПЛАН РАБОТЫ
Задание 1. Определить электрические параметры четырехпроводной трехфазной цепи при симметричной и несимметричной нагрузке, соединенной по схеме «звезда» с нулевым (нейтральным) проводом.
1. Собрать электрическую схему (рис.29).
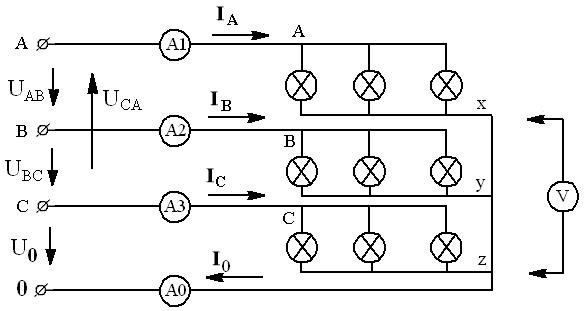
Рис.29. Схема лабораторной установки: А-х, В-y, C-z - трехфазный ламповый реостат, установленный на стенде; А1 - амперметр на ток 1–2 А; А2, А3, А0 - амперметры на ток 0,25–0,5–1 А; V – вольтметр на 75-150-300-600 В.
2. Установить симметричную нагрузку фаз, включив по пять ламп в каждой фазе, и измерить IA, IB, IC, IN, UA, UB, UC, UAB, UBC, UCA.
3. Установить несимметричную нагрузку фаз, включив 5 ламп в фазе А, 4 лампы в фазе «В» и 3 лампы в фазе «С» и осуществить измерения электрических параметров, указанных в п.2.
4. Вычислить электрические параметры, указанные в табл.7.
5. занести результаты измерений и вычислений в табл.7.
Задание 2. Определить электрические параметры трехпроводной трехфазной цепи при симметричной и несимметричной нагрузке, соединенной по схеме «звезда» без нулевого (нейтрального) провода.
1. Собрать электрическую схему (рис.30).

Рис.30. Схема лабораторной установки: А-х, В-y, C-z - трехфазный ламповый реостат, установленный на стенде; А1 - амперметр на ток 1–2 А; А2, А3 - амперметры на ток 0,25–0,5–1 А; V – вольтметр на 75-150-300-600 В; W1 и W2 - ваттметры на напряжение 75−150−300−600 В и ток 1−2,5−5 А.
2. Установить симметричную нагрузку, включив по пять ламп в каждой фазе, и измерить линейные и фазные напряжения, фазные токи, активные мощности.
3. Установить несимметричную нагрузку фаз, включив 5 ламп в фазе А, 4 лампы в фазе «В» и 3 лампы в фазе «С» и измерить электрические параметры, указанные в п.2.
4. Вычислить электрические параметры, указанные в табл.8.
5. Занести результаты измерений и вычислений в табл.8.
Содержание отчета.
1. Схемы измерений (рис.29 и 30) с обозначениями используемых приборов.
2. Расчет электрических параметров.
3. Таблицы 7 и 8 с результатами измерений и вычислений.
4. Построенные в масштабе топографические векторные диаграммы (две к заданию 1 по данным п.1-2 табл.7 в соответствии с рис. 21 и 22 и две к заданию 2 по данным пп.1-2 табл.8 в соответствии с рис. 24 и 25.
Таблица 7
| Измеренные величины | Вычисленные величины | |||||||||||||
| I A | I В | I С | I 0 | U A | U В | U С | U AВ | U ВС | U СА | U Л/ U Ф | Р А | Р В | Р С | Р |
| А | А | А | А | В | В | В | В | В | В | В | Вт | Вт | Вт | Вт |
| 0,6 | 0,6 | 0,6 | ||||||||||||
| 0,6 | 0,45 | 0,35 | 0,21 |
Таблица 8
| Измеренные величины | Вычисленные величины | |||||||||||||||
| I A | I В | I С | U A | U В | U С | U AВ | U ВС | U СА | Р 1(W 1) | Р 2(W 2) | U Л/ U Ф | Р А | Р В | Р С | Р расч | Р (W 1+ W 2) |
| А | А | А | В | В | В | В | В | В | Вт | Вт | В | Вт | Вт | Вт | Вт | Вт |
| 0,6 | 0,6 | 0,6 | ||||||||||||||
| 0,525 | 0,475 | 0,375 |
Контрольные вопросы
1. Как относятся друг с другом ЭДС, составляющие трехфазную систему?
2. Как соединяются обмотки генератора при соединении «звездой»?
3. Чем отличается схема четырехпроводной системы трехфазного тока от схемы трехпроводной системы?
4. Что соединяет нулевой (нейтральный) провод?
5. Что такое линейные и фазные токи и напряжения и каковы соотношения между ними при соединении звездой в векторной форме?
6. Как связаны линейные и фазные напряжения в четырехпроводной системе трехфазного тока?
7. Что такое симметричная и несимметричная нагрузка?
8. Чему равна геометрическая сумма токов в четырехпроводной трехфазной системе при симметричной нагрузке?
9. Чему равен ток в нулевом проводе при симметричной нагрузке?
10. отличаются ли токи и напряжения в четырехпроводной и трехпроводной системах трехфазного тока при одинаковой симметричной нагрузке?
11. При какой нагрузке необходимо включить в трехфазную систему нулевой провод и зачем?
12. Как определить ток в нулевом проводе четырехпроводной системы при несимметричной нагрузке, зная линейные токи?
13. При каких условиях будут равны напряжения на всех фазах нагрузки в трехпроводной трехфазной системе?
14. Каков характер нагрузки в осветительных сетях?
15. Какую систему трехфазного тока нужно использовать в осветительных сетях и почему?
16. какую мощность можно определить методом двух ваттметров?
17. Чему равна активная мощность цепи при применении метода двух ваттметров?
18. В каких системах трехфазного тока может быть применен метод двух ваттметров?
19. Можно ли определить полную мощность трехфазной системы, используя метод двух ваттметров?
20. Можно ли определить коэффициент мощности трехфазной системы, используя метод двух ваттметров?