ТЕМА 5. МЕТОДЫАНАЛИЗА ВРЕМЕННЫХ РЯДОВ
Лекция 9. Компоненты временного ряда. Модели тренда. Индексы сезонности.
Основная цель анализа временных рядов – прогнозирование будущего состояния объекта (процесса), получение базовой информации для принятия управленческих решений. Для реализации прогноза необходима модель, адекватно описывающая поведение ряда. Выбор конкретной модели определяется характером изменения уровней ряда, присутствием тех или иных компонент.
Компоненты временного ряда
Уровни рядов динамики формируются под влиянием множества факторов. Одни из них действуют стабильно на протяжении длительного периода времени и формируют основную тенденцию временного ряда, которая называется трендом.
Ряд факторов влияют на уровни ряда с определенной периодичностью, циклически (экономические циклы, циклы солнечной активности и т.п.). Для обнаружения и анализа влияния циклических факторов необходимы достаточно длинные временные ряды.
Повторяющиеся колебания уровней внутри года – результат влияния сезонных факторов.
Влияние случайных факторов на уровни ряда происходит без какой-либо периодичности, и, следовательно, не поддается измерению.
Исходя из вышесказанного, уровень временного ряда может быть представлен как функция четырех компонент:
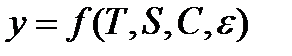 , (9.1)
, (9.1)
где T – трендовая компонента; S – сезонная компонента; C – циклическая компонента; 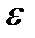 – случайная компонента.
– случайная компонента.
Чем сильнее влияние не трендовых компонент, тем сложнее выявить и описать основную тенденцию ряда, а именно это является центральной задачей при построении моделей временных рядов.
Сгладить влияние на уровни ряда не трендовых компонент позволяет процедура выравнивания временных рядов. Суть этой процедурысостоит в замене фактических уровней изучаемого ряда теоретическими. Теоретические уровни –это уровни, в той или иной мере очищенные от влиянияне трендовых компонент и полученные врезультате определенных расчетов, преобразований исходного ряда.
В арсенале статистики два приема выравнивания временных рядов: механическое выравнивание и аналитическое.
Механическое выравнивание может быть осуществлено:
«Методом укрупнения интервалов. Данный метод предполагает объединение временных периодов и расчет по ним либо суммарных значений показателей, либо средних величин. Например, если ряд был представлен данными по месяцам, то выравнивание будет заключаться в объединении уровней и представлении ряда данными по кварталам. Укрупнение временных интервалов приведет к снижению степени колеблемости уровней и к более отчетливому проявлению тенденции.
«Метод скользящей средней. Данный метод предполагает расчет среднего уровня за определенный временной интервал (например, 3-5 лет), и дальнейшее скольжение интервала по временному ряду (напомним, что в средних величинах происходит взаимопогашение влияния случайных факторов). Полученные средние (выровненные) значения уровней относятся к середине интервала, по которому рассчитываются средние. Так, если период скольжения три года, первая средняя величина будет рассчитана:
 , а полученное среднее значение будет отнесено ко второму периоду. Далее рассчитывается средняя величина следующих 3-х уровней:
, а полученное среднее значение будет отнесено ко второму периоду. Далее рассчитывается средняя величина следующих 3-х уровней:
 , полученное значение будет отнесено к третьему периоду ряда и т.д.
, полученное значение будет отнесено к третьему периоду ряда и т.д.
Если период скольжения – четная величина, то применяют метод центрирования. Этот прием выражается в подсчете средней арифметической величины из значений, полученных по двум шагам скольжения.
Увеличение периода скольжения позволяет более отчетливо проявиться основной тенденции, однако результатом является существенно укороченный временной ряд, что неблагоприятно может сказаться на качестве трендовой модели.
Аналитическое выравнивание позволяет не только выявить основную тенденцию ряда, но и получить аналитическую форму тренда в виде уравнения.
Уравнение (модель) тренда – это парное уравнение регрессии, в качестве фактора в котором выступает время (t). Переменная «t» задается простой последовательностью чисел от 1 до n. В общем виде уравнение может быть записано:
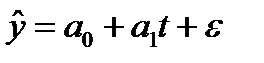 , (9.2)
, (9.2)
где 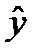 – зависимая переменная, условное среднее значение уровней временного ряда;
– зависимая переменная, условное среднее значение уровней временного ряда;  и
и 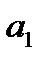 – параметры уравнения тренда; t – независимая переменная, фактор-время;
– параметры уравнения тренда; t – независимая переменная, фактор-время; 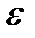 - случайная составляющая.
- случайная составляющая.
Расчет параметров трендовой модели осуществляется с использованием метода наименьших квадратов (о котором говорилось в теме регрессионного анализа).
Центральной проблемой построения трендовой модели является выбор типа уравнения тренда, наилучшим образом описывающего основную тенденцию изучаемого ряда. Для решения этой задачи могут быть использованы:
· графическое представление временного ряда;
· метод конечных разностей;
· формализованный подход, т.е. метод критериев.
При графическом представлении временных рядов по оси абсцисс откладываются периоды или моменты времени, по оси ординат – значения уровней ряда. Расположение эмпирической линии тренда на графике позволяет выдвинуть гипотезу о типе уравнения тренда.
Метод конечных разностей основан на свойствах математических функций и анализе показателей изменения уровней временных рядов. Так, если примерно постоянными являются первые разности (абсолютные приросты), для описания тренда можно воспользоваться полиномом первой степени (линейной функцией). Если примерно постоянны вторые разности (показатели ускорения), то следует использовать полином второй степени и т.д.
В настоящее время выбор функции, для описания тренда, как правило, формализован, т.е. осуществляется с использованием статистических критериев на базе пакетов прикладных программ. Аналитик одновременно строит несколько уравнений тренда, а затем, исходя из значений определенных критериев, выбирает одно, дающее лучшую аппроксимацию.
В качестве критериев выбора модели тренда могут быть использованы следующие характеристики:
1. Минимальная сумма квадратов отклонений теоретических значений уровней ряда (полученных на основе уравнения тренда) от фактических:
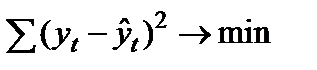 , (9.3)
, (9.3)
где yt– фактическое значение уровня ряда периода t; 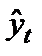 - теоретическое значение уровень ряда периода t.
- теоретическое значение уровень ряда периода t.
2. Минимальная величина остаточной дисперсии (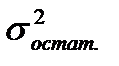 )
)  или минимальное значение среднеквадратической ошибки уравнения тренда
или минимальное значение среднеквадратической ошибки уравнения тренда 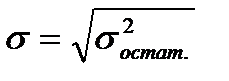 .
.
3. Минимальное значение средней ошибки аппроксимации:
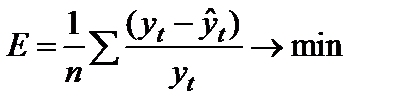 . (9.4)
. (9.4)
4. Максимальное значение F-критерия Фишера, оценивающего значимость уравнения в целом (см. тему регрессионного анализа): 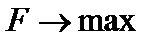 .
.
5. Максимальное значение коэффициента детерминации, характеризующего долю объясненной дисперсии в общей дисперсии результативного признака: 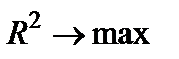 .
.
Продолжая анализировать динамику показателя обеспеченности жильем, построим три уравнения тренда, используя линейную функцию, параболу второго порядка и экспоненту. Результаты расчетов, выполненных в пакете STATISTICA, представлены в таблицах 9.1, 9.2, 9.3 (структура и анализ таблиц трендовых моделей аналогичны таблицам парных уравнений регрессии.См. соответствующую лекцию.).
Таблица 9.1 - Линейный тренд временного ряда показателей общей площади жилых помещений, приходящейся в среднем на одного жителя, м.кв./чел.
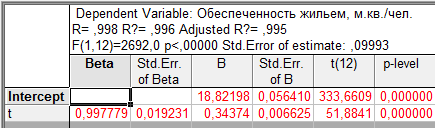
Графа «В» таблицы содержит значения параметров уравнения, t- статистика позволяет оценить статистическую значимость параметров модели. В верхней части таблицы приведены значения коэффициента корреляции (R), коэффициента детерминации (R?= 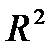 ), скорректированного коэффициента детерминации (AdjustedR?) и F - критерия Фишера (F).
), скорректированного коэффициента детерминации (AdjustedR?) и F - критерия Фишера (F).
Уравнение может быть записано: y = 18,82 + 0,34 t.
Таблица 9.2 - Параболический тренд временного ряда показателей общей жилой площади, приходящейся в среднем на одного жителя, м.кв./чел.
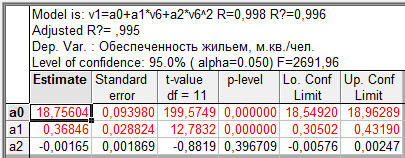
Расчет характеристик, содержащихся в таблицах 9.2 и 9.3, выполнен в процедуре нелинейного оценивания программыSTATISTICA, в этих таблицах значения параметров уравнения находятся в графе Estimate, в двух последних графах дополнительно приводятся значения границ доверительных интервалов для генеральных параметров.
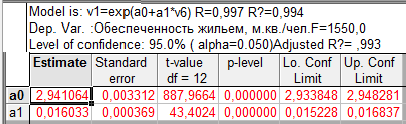
Таблица 9.3 - Экспоненциальный тренд временного ряда показателей общей жилой площади, приходящейся в среднем на одного жителя, м.кв./чел.
Для анализа результатов расчетов и выбора модели тренда построим сводную таблицу 9.4.
Таблица 9.4 - Оценка статистической значимости параметров и уравнений тренда
| Уравнение тренда | 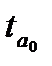
| 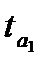
| 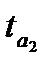
| 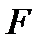
| 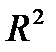
|
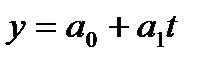
| 333,66 | 51,88 | - | 2692,0 | 0,995 |
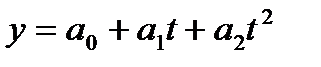
| 199,58 | 12,78 | 0,88 | 2691,96 | 0,995 |
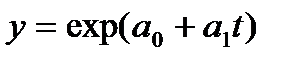
| 887,97 | 43,40 | - | 1550,0 | 0,994 |
Параметры линейной и экспоненциальной моделей статистически значимы, поскольку расчетное значение t - статистики для каждого параметра больше табличного значения t - статистики с учетом принятого уровня значимости и соответствующего числа степеней свободы ( (0,05; 12)=2,179). Расчетные значения F - критерия, также превышающие табличное значение (
(0,05; 12)=2,179). Расчетные значения F - критерия, также превышающие табличное значение ( (1,12)=4,75), следовательно, уравнения в целом и значения коэффициента детерминации статистически значимы, т.е. данные модели позволяют объяснить существенную часть вариации зависимой переменной - показателя обеспеченности жильем населения России.
(1,12)=4,75), следовательно, уравнения в целом и значения коэффициента детерминации статистически значимы, т.е. данные модели позволяют объяснить существенную часть вариации зависимой переменной - показателя обеспеченности жильем населения России.
В уравнении полинома второго порядка параметр 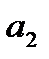 статистически не значим, поскольку
статистически не значим, поскольку  (0,88)<
(0,88)<  ((0,05; 11)=2,201), следовательно, несмотря на то, что уравнение в целом статистически значимо (
((0,05; 11)=2,201), следовательно, несмотря на то, что уравнение в целом статистически значимо ( >
>  (2,11)=3,98), оно не может быть использовано для прогнозирования значений зависимой переменной.
(2,11)=3,98), оно не может быть использовано для прогнозирования значений зависимой переменной.
Выбор между двумя статистически значимыми уравнениями осуществляется на основе значений коэффициентов детерминации, характеризующих долю объясненной дисперсии в общей дисперсии зависимой переменной. Предпочтение следует отдать линейной модели, которой соответствует большее значение коэффициента детерминации (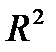 =0,995).
=0,995).
Уравнение тренда может бытьпризнано моделью, пригодной для прогнозирования, если оно отвечает следующим требованиям:
· уравнение в целом статистически значимо (оценка по F-критерию);
· все параметры уравнения статистически значимы (оценка по t-статистике);
· в остатках уравнения отсутствует автокорреляция.
Процедуры оценки статистической значимости уравнения в целом и его параметров подробно рассмотрены в разделе КРА. Остановимся на оценке автокорреляции в остатках модели.
Остатки – это разность между фактическими значениями уровней временного ряда и выровненными (теоретическими) значениями, полученными по уравнению тренда.
Фактические уровни: Теоретические
(выровненные) уровни: Остатки:
y1 
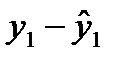

y2 

y3 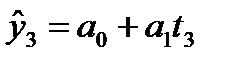

…… ………………………. ……………..
yt 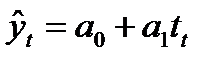

Рисунок 9.1 - Определение величины остатков модели временного ряда
Автокорреляция остатков – это зависимость остатков периода t от остатков предшествующих периодов (t-i). Если построенное уравнение обеспечивает удовлетворительную аппроксимацию, то отклонения от тренда (остатки) должны носить случайный характер и в их последовательности не должно быть корреляции.
Исследование автокорреляции остатков трендовой модели имеет особое значение, если ставится задача прогнозирования поведения временного ряда. Дело в том, что наличие автокорреляции свидетельствует о наличии тенденции в остатках, т.е. о сохранении в них части полезной информации. Поскольку основная задача построения трендовой модели – как можно более полно описать основную тенденцию изучаемого ряда – сохранение тенденции в остатках, говорит о том, что модель не может быть признана пригодной для получения прогнозаудовлетворительногокачества.
Оценка автокорреляции в остатках может быть проведена на основе коэффициентов автокорреляции, либо с использованием специального критерия - критерияДарбина-Уотсона.
Если остатки периода t обозначить 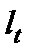 , а остатки предшествующего периода
, а остатки предшествующего периода 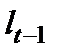 , то коэффициент автокорреляции, предложенный М. Езекиэлом и К. Фоксом, будет рассчитываться:
, то коэффициент автокорреляции, предложенный М. Езекиэлом и К. Фоксом, будет рассчитываться:
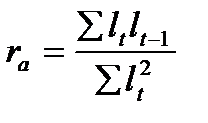 . (9.5)
. (9.5)
Коэффициент автокорреляции изменяется в пределах:  , как и обычный парный коэффициент корреляции. Близость значения коэффициента к нулю означает отсутствие автокорреляции, к единице – наличие автокорреляции в остатках.
, как и обычный парный коэффициент корреляции. Близость значения коэффициента к нулю означает отсутствие автокорреляции, к единице – наличие автокорреляции в остатках.
По достаточно большим временным рядам могут быть рассчитаны коэффициенты автокорреляции разных порядков, т.е. коэффициенты, оценивающие зависимость не только между остатками соседних периодов, но между остатками, разделенными двумя, тремя и б о льшим числом временных интервалов. Интервал, разделяющий зависимые остатки, называют лагом. Величина лага определяет порядок коэффициента автокорреляции. Последовательность коэффициентов автокорреляции разного порядка называется автокорреляционной функцией, которая характеризует зависимость величины коэффициентов автокорреляции от величины лага.
В таблице 9.5 приведены фактические (ObservedValue), теоретические (PredictedValue), т.е. рассчитанные по линейной модели, значения показателя обеспеченности жильем и величины остатков (Residual), равные разности значений двух первых столбцов.
Таблица 9.5 - Фактические, теоретические уровни и остатки линейного тренда временного ряда показателей общей жилой площади, приходящейся в среднем на одного жителя, м.кв./чел.
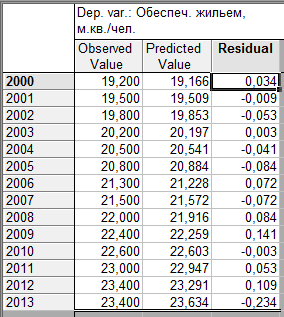
Для оценки автокорреляции остатков рассчитаем коэффициенты автокорреляции. Поскольку анализируемый временной ряд содержит всего 14 уровней, то рассчитаем коэффициенты лишь трех порядков: первого, который покажет степень корреляционной зависимости между смежными значениями остатков; второго, т.е. будет дана оценка зависимости между остатками, разделенными двумя годами; третьего порядка - оценка корреляционной связи между остатками с интервалом в три года.
Автокорреляционная функция остатков линейной модели и ее графическое отображение представлены на рисунке 9.2.
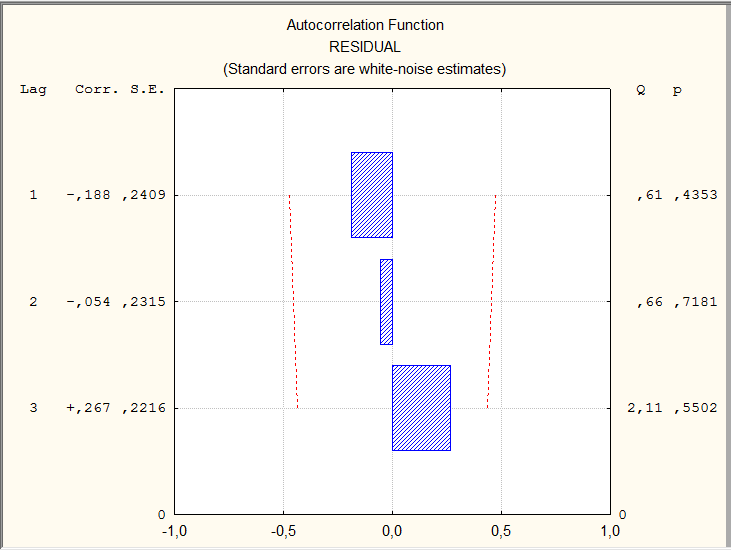
Рисунок 9.2 - Автокорреляционная функция остатков линейной модели временного ряда показателей общей жилой площади, приходящейся в среднем на одного жителя, м.кв./чел.
Графическое отображение коэффициентов автокорреляции (прямоугольники) сопровождается числовыми значениями этих характеристик (графа Corr.): коэффициент автокорреляции первого порядка 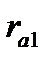 = - 0,188, второго
= - 0,188, второго 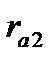 = -0,054, третьего
= -0,054, третьего 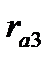 =0,267. На порядок коэффициентов автокорреляции указывает величина лага (Lag). Статистическую значимость коэффициентов можно оценить, рассчитав t - статистику:
=0,267. На порядок коэффициентов автокорреляции указывает величина лага (Lag). Статистическую значимость коэффициентов можно оценить, рассчитав t - статистику:
 (9.6)
(9.6)
где: 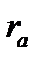 – коэффициент автокорреляции,
– коэффициент автокорреляции, 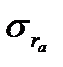 - стандартная ошибка коэффициента автокорреляции (графаS.E.).
- стандартная ошибка коэффициента автокорреляции (графаS.E.).
В результате расчетов получены следующие величины t - статистики:  =0,78,
=0,78,  =0,23 и
=0,23 и 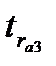 =1,2. Все значения t - статистики не превышают табличного значения (
=1,2. Все значения t - статистики не превышают табличного значения ( (0,05)=2,179), которое находится по таблице распределения Стьюдента, поскольку объем данных менее 30. Таким образом, полученные значения коэффициентов автокорреляции статистически не значимы. Проведенная оценкаговорит об отсутствии автокорреляции в остатках линейной модели тренда. Этот вывод подтверждается и графическим представлением автокорреляционной функции: величины коэффициентов, представленные прямоугольниками, не выходят за пределы доверительных интервалов, обозначенных пунктирными линиями.
(0,05)=2,179), которое находится по таблице распределения Стьюдента, поскольку объем данных менее 30. Таким образом, полученные значения коэффициентов автокорреляции статистически не значимы. Проведенная оценкаговорит об отсутствии автокорреляции в остатках линейной модели тренда. Этот вывод подтверждается и графическим представлением автокорреляционной функции: величины коэффициентов, представленные прямоугольниками, не выходят за пределы доверительных интервалов, обозначенных пунктирными линиями.
Рассмотрим еще один метод оценки автокорреляции в остатках - критерий Дарбина-Уотсона (D-W). Используя введенные ранее обозначения (см. 9.5), критерий может быть рассчитан следующим образом:
 . (9.10)
. (9.10)
Между критерием Дарбина-Уотсона и коэффициентом автокорреляции существует следующее соотношение: 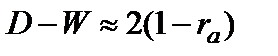 .
.
Исходя из этого соотношения, очевидно, что если:
ra=0, то D-W=2;
ra=1, то D-W=0;
ra=-1, то D-W=4.
Таким образом, значение критерия может изменяться в пределах:
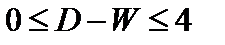 . (9.11)
. (9.11)
Близость D-W к 0 и к 4 означает присутствие автокорреляции в остатках, к 2 – ее отсутствие.
КритерийДарбина-Уотсона табулирован. По таблицам, исходя из числа уровней динамического ряда и числа факторов в уравнении тренда, находят границы значения критерия:  ,
, 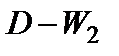 - нижняя и верхняя границы критерия.
- нижняя и верхняя границы критерия.
Если:
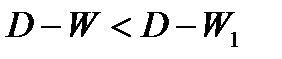 - автокорреляция в остатках присутствует;
- автокорреляция в остатках присутствует;
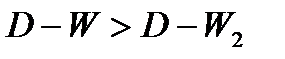 - автокорреляция в остатках отсутствует;
- автокорреляция в остатках отсутствует;
Если 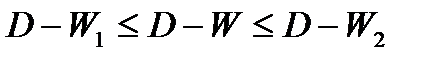 - возникает ситуация неопределенности, которая требует дальнейшего исследования ряда в условиях увеличения объема данных, или использования иного типа модели.
- возникает ситуация неопределенности, которая требует дальнейшего исследования ряда в условиях увеличения объема данных, или использования иного типа модели.
Оценивая остатки линейной модели рассматриваемого примера, в программе STATISTICA было получено значение критерия Дарбина-Уотсона=1,91. Табличные значения верхней и нижней границ критерия (см. приложение...)следующие:  = 1,05,
= 1,05, 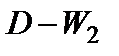 =1,35. Поскольку расчетное значение критерия (1,91) превышает верхнюю границу табличного значения (1,35), подтверждается вывод об отсутствии автокорреляции в остатках модели тренда временного ряда показателей общей жилой площади, приходящейся в среднем на одного жителя, м.кв./чел.
=1,35. Поскольку расчетное значение критерия (1,91) превышает верхнюю границу табличного значения (1,35), подтверждается вывод об отсутствии автокорреляции в остатках модели тренда временного ряда показателей общей жилой площади, приходящейся в среднем на одного жителя, м.кв./чел.
Таким образом, весь комплекс требований, необходимых для признания модели тренда пригодной для прогнозирования, выполнен: уравнение тренда статистически значимо, параметры статистически значимы, в остатках модели отсутствует автокорреляция.
Регрессионную модель тренда, отвечающую всем формальным требованиям, можно использовать для оценки величины переменной y в последующие периоды времени t. Чтобы получить, так называемый, точечный прогноз при заданном значении t, вычисляется значение построенной функции регрессии в точке t.
В рассматриваемом примере исходный временной ряд включал 14 уровней (данные с 2000 по 2013 годы), следовательно, точечный прогноз может быть выполнен на 15-й период(на 2014 год) и дальнейшие периоды. Подставляя в уравнение значение t=15 (y=18,82 + 0,34*15), получаем, что прогнозируемое среднее значение показателя обеспеченности жильем в России в 2014 году составит 23,92 м.кв./чел.
Однако следует помнить, что уравнение тренда описывает лишь общую тенденцию изменения показателя. Фактическая реализация событий отличается от прогнозируемой. Совпадение фактических и прогнозных значений маловероятно. Уравнение тренда всегда содержит ошибку, которую принято оценивать среднеквадратической (стандартной) ошибкой тренда:
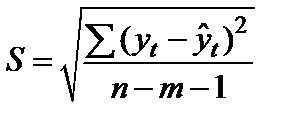
, (9.12)
где 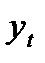 - фактическое значение уровня ряда периода t;
- фактическое значение уровня ряда периода t; 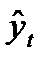 - значение уровня ряда периода t, рассчитанное по уравнению тренда; n – число уровней ряда; m – число факторов, включенных в уравнение;n-m-1 –число степеней свободы остаточной дисперсии.
- значение уровня ряда периода t, рассчитанное по уравнению тренда; n – число уровней ряда; m – число факторов, включенных в уравнение;n-m-1 –число степеней свободы остаточной дисперсии.
Как видим, средняя ошибка тренда – это корень квадратный из остаточной дисперсии, которая оценивает степень колеблемости уровней временного ряда (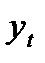 ) относительно тренда (
) относительно тренда (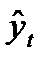 ). Среднеквадратическая ошибка тренда, таким образом, характеризует: насколько в среднем отличаются значения уровней ряда, рассчитанные на основе уравнения, от их фактических значений.
). Среднеквадратическая ошибка тренда, таким образом, характеризует: насколько в среднем отличаются значения уровней ряда, рассчитанные на основе уравнения, от их фактических значений.
С учетом ошибки тренда может быть рассчитан доверительный интервал прогноза:
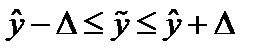 (9.13)
(9.13)
где 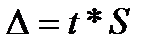 - предельная ошибка;t – коэффициент доверия, величина которого находится по таблице Стьюдента, исходя из принятого исследователем уровня значимости и соответствующего числа степеней свободы (n-m-1).
- предельная ошибка;t – коэффициент доверия, величина которого находится по таблице Стьюдента, исходя из принятого исследователем уровня значимости и соответствующего числа степеней свободы (n-m-1).
При выполнении расчетов с использованием специализированных компьютерных программ, величина ошибки определяется в одной процедуре с расчетом значений параметров уравнения. В таблице 9.1 представлено значение стандартной ошибка линейного тренда (St.Errorofesimate): S=0,0999. Величина коэффициента доверия, исходя из уровня значимости 0,05 и числа степеней свободы 12 (14-1-1), равна 2,179 (см. прил. Табл. Стьюд.), тогда
 2,179 * 0,0999 = 0,218. Доверительный интервал будет рассчитан:
2,179 * 0,0999 = 0,218. Доверительный интервал будет рассчитан:  и окончательно -
и окончательно - 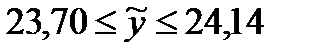 . Таким образом, с вероятностью 0,95 можно утверждать, что в среднем показатель обеспеченности жильем в регионах России в 2014 году будет не ниже 23,7 и не выше 24,14 квадратных метров на человека (заметим, что фактическое значение показателя в 2014 году по данным Росстата составило 23,7 квадратных метра на человека).
. Таким образом, с вероятностью 0,95 можно утверждать, что в среднем показатель обеспеченности жильем в регионах России в 2014 году будет не ниже 23,7 и не выше 24,14 квадратных метров на человека (заметим, что фактическое значение показателя в 2014 году по данным Росстата составило 23,7 квадратных метра на человека).
Прогнозирование на основе временных рядов называют экстраполяцией - продлением в будущее тенденции, сложившейся в прошлом. Следовательно, доверять результатам прогнозирования можно при условии, что факторы, повлиявшие на формирование тенденции в прошлом, неизменно будут действовать и в будущем. Еще один практический совет, выработанный статистикой: период упреждения, т.е. период на который делается прогноз, не должен превышать 1/3 длины ряда, на основе которого построена модель.