Уравнение, неравенство, система обладают свойством алгебраической симметрии, если они не меняют своего вида при замене местами или изменения знака переменных.
Если уравнение (неравенство, система) с параметром обладает свойством алгебраической симметрии, то часто требуется определить при каких значениях параметра уравнение (неравенство, система) имеет единственное решение.
Например, уравнение  где
где 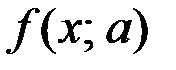 чётная функция, а – параметр, обладает свойством алгебраической симметрии, так как при изменении знака переменной оно не меняют своего вида. Если решением уравнения является
чётная функция, а – параметр, обладает свойством алгебраической симметрии, так как при изменении знака переменной оно не меняют своего вида. Если решением уравнения является  , то и
, то и 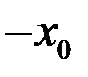 одновременно является решением этого уравнения. Рассматриваемое уравнение может иметь единственное решение, только в случае, если
одновременно является решением этого уравнения. Рассматриваемое уравнение может иметь единственное решение, только в случае, если  Необходимым условием существованием единственного решения рассматриваемого уравнения является выполнения условия
Необходимым условием существованием единственного решения рассматриваемого уравнения является выполнения условия 
Например, система с параметром а  обладает свойством алгебраической симметрии, если система не меняется при замене у на х и х на у (график каждого уравнения имеет ось симметрии
обладает свойством алгебраической симметрии, если система не меняется при замене у на х и х на у (график каждого уравнения имеет ось симметрии 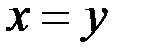 ). Тогда вместе с решением
). Тогда вместе с решением  система имеет решение
система имеет решение  Рассматриваемая система может иметь единственное решение, только в случае, если
Рассматриваемая система может иметь единственное решение, только в случае, если 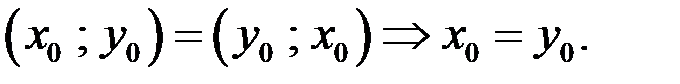 Тогда необходимым условием существованием единственного решения рассматриваемой системы является выполнения условия
Тогда необходимым условием существованием единственного решения рассматриваемой системы является выполнения условия 
Если уравнение (неравенство, система) с параметром а обладает свойством алгебраической симметрии, то нахождение единственного решения состоит из двух этапов:
1) Необходимое условие. Используя свойство алгебраической симметрии, находятся значения параметра, при которых уравнение (неравенство, система) может иметь единственное решение.
2) Достаточное условие. Решается уравнение (неравенство, система) при параметрах, найденных в пункте 1). Параметры, при которых рассматриваемое уравнение (неравенство, система) имеет единственное решение, удовлетворяют условию задачи.
31. При каких значениях параметра а,имеет нечётное число корней уравнение  ?
?
Решение. Так как функция 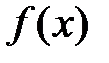 =
=  чётная, то уравнение (1) имеет нечётное число корней тогда и только тогда, когда одним из корней является
чётная, то уравнение (1) имеет нечётное число корней тогда и только тогда, когда одним из корней является  .
.
Корнем исходного уравнения является  , если
, если

Итак, 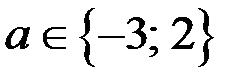 удовлетворяют условию задачи.
удовлетворяют условию задачи.
Ответ. 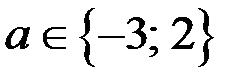 .
.
32. При каких значениях параметра а,имеет единственное решение уравнение 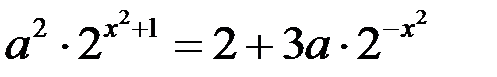 ?
?
Решение. 1. Имеем

Так как функция  чётная, то исходное уравнение имеет нечётное число решений тогда и только тогда, когда одним из корней уравнения является
чётная, то исходное уравнение имеет нечётное число решений тогда и только тогда, когда одним из корней уравнения является  .
.
Корнем уравнения (1) является  , если
, если

2. Определим, сколько решений имеет исходное уравнение, если  .
.
а) Если  то исходное уравнение принимает вид
то исходное уравнение принимает вид
 .
.
Итак, если  то исходное уравнение имеет три корня.
то исходное уравнение имеет три корня.
а) Если  то исходное уравнение принимает вид:
то исходное уравнение принимает вид:

Итак, если  то исходное уравнение имеет один корень.
то исходное уравнение имеет один корень.
Ответ.  .
.
33. Найдите все значения параметра а,при которых имеет единственное решение уравнение  .
.
Решение. 1. Легко проверить, если  то уравнение (1) не имеет решений.
то уравнение (1) не имеет решений.
2. Пусть 
Пусть  .
.
Так как  , то функция
, то функция 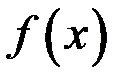 чётная.
чётная.
1) Уравнение (1) может иметь нечётное число решений, если корнем уравнения является  .
.
Корнем уравнения (1) является  , если
, если

2) Определим, сколько решений имеет уравнение (1), если 
Если 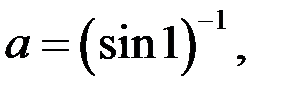 то уравнение (1) принимает вид
то уравнение (1) принимает вид

Очевидно, 
Оценим правую часть уравнения (2).
Так как функция 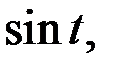 если
если  возрастает и эта функция нечтная, то
возрастает и эта функция нечтная, то

Так как левая часть уравнения (2) не меньше  , а правая – не больше
, а правая – не больше  , то уравнение (2) равносильно системе
, то уравнение (2) равносильно системе
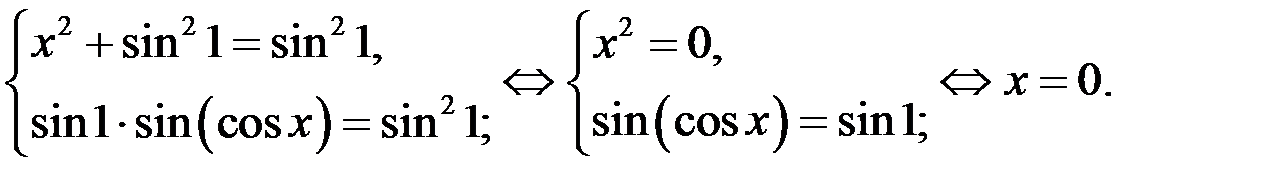
Итак, если  то исходное уравнение имеет один корень.
то исходное уравнение имеет один корень.
Ответ.  .
.
34. Найдите все значения параметра а, при которых имеет единственное решение уравнение 
Решение. 1. Левая часть уравнения (1) – чётная функция. Если решением уравнения (1) является  , то и
, то и 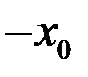 одновременно является решением этого уравнения. Поэтому уравнение (1) может иметь единственное решение, если решением уравнения является
одновременно является решением этого уравнения. Поэтому уравнение (1) может иметь единственное решение, если решением уравнения является  .
.
2. Решением уравнения (1) является  , если
, если

Так как последняя система не имеет решений, то ни при каких значениях параметра а уравнение (1) не имеет единственного решения.
Ответ. Не имеет единственного решения.
35. Найдите все значения параметра а, при которых имеет единственное решение неравенство
 .
.
Решение. 1. Обе части неравенства (1) – чётные функции. Если решением неравенства (1) является  , то и
, то и 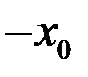 одновременно является решением этого неравенства. Поэтому неравенство может иметь единственное решение, если решением неравенства является
одновременно является решением этого неравенства. Поэтому неравенство может иметь единственное решение, если решением неравенства является  .
.
2. Решением неравенства (1) является  , если
, если

1) Определим, сколько решений имеет неравенство (1), если 
Отметим: если 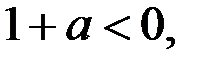 то
то 
Имеем  Так как последнее неравенство выполняется при любом значении х,
Так как последнее неравенство выполняется при любом значении х,
то  не удовлетворяют условию задачи.
не удовлетворяют условию задачи.
2) Если  то неравенство (1) принимает вид
то неравенство (1) принимает вид


Итак, если  то неравенство (1) имеет одно решение.
то неравенство (1) имеет одно решение.
Ответ.  .
.
36. Найдите все значения параметра а, при которых имеет единственное решение система 
Решение. 1. Из второго уравнения системы следует, что  и
и 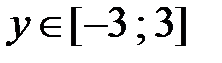 . Очевидно, точки
. Очевидно, точки 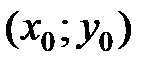 и
и  одновременно удовлетворяют первому и второму уравнениям системы. Откуда следует, что система (1) имеет нечётное число решений тогда и только тогда, когда среди решений находится решение
одновременно удовлетворяют первому и второму уравнениям системы. Откуда следует, что система (1) имеет нечётное число решений тогда и только тогда, когда среди решений находится решение 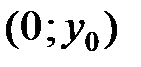 . Если
. Если 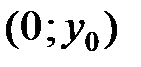 решение системы (1), то из
решение системы (1), то из
системы (1) следует, что 
Из полученной системы следует: решением системы (1) является точка  , если
, если  , или точка
, или точка  , если
, если  .
.
2. Определим, сколько решений имеет система (1), если  .
.
а) Если  , то система (1) принимает вид
, то система (1) принимает вид

Замечание. Целые корни уравнения  с целыми коэффициентами являются делителями свободного члена.
с целыми коэффициентами являются делителями свободного члена.
Рассмотрим первое уравнение системы (2). Очевидно, одним из корней этого уравнения является 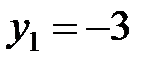 .
.
Делителями свободного члена уравнения  (2) являются:
(2) являются:  Проверкой убеждаемся, что корнем уравнения (2) является
Проверкой убеждаемся, что корнем уравнения (2) является  .
.
Итак, первое уравнение системы (1) имеет не менее двух корней, которые удовлетворяют условию 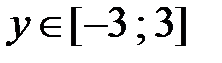 . Система (2) имеет не менее трёх решений:
. Система (2) имеет не менее трёх решений:  Это означает, что
Это означает, что 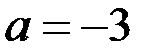 не удовлетворяет условию задачи.
не удовлетворяет условию задачи.
б) Если  , то исходная система принимает вид
, то исходная система принимает вид

Из первого уравнения системы (3) следует, что  . А так как
. А так как 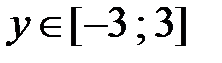 , то
, то  Легко проверить, что системе (3) удовлетворяет только точка
Легко проверить, что системе (3) удовлетворяет только точка  . Тогда
. Тогда  удовлетворяет условию задачи.
удовлетворяет условию задачи.
Ответ.  .
.
37. Найдите все значениях параметра а, при которых имеет единственное решение система 
Решение. 1. Так как  то
то 
Исходная система перепишется в виде

Легко проверить: если  решение системы (1), то и
решение системы (1), то и 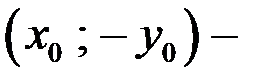 решение системы (1). Тогда система (1) может иметь единственное решение, если решением системы является
решение системы (1). Тогда система (1) может иметь единственное решение, если решением системы является 
2. Если  решение системы (1), то система принимает вид
решение системы (1), то система принимает вид
 3. Определим, число решений системы (1), если
3. Определим, число решений системы (1), если 
1) Если  то система (1) принимает вид
то система (1) принимает вид
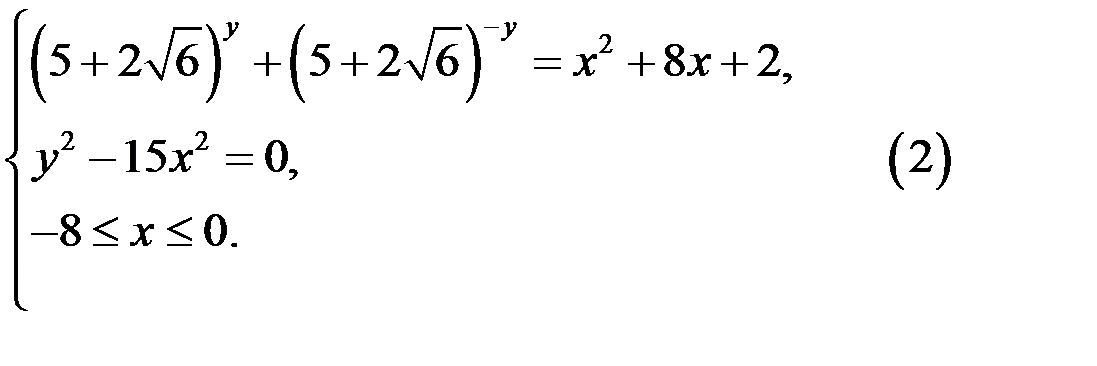
Рассмотрим первое уравнение системы (2).
Левая часть уравнения не меньше двух (если  то
то  ) и равна двум, если
) и равна двум, если  Правая часть уравнения не больше двух, если
Правая часть уравнения не больше двух, если 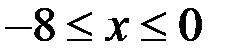 (действительно, имеем
(действительно, имеем  ) и равна двум, если
) и равна двум, если  . Итак, решением первого уравнения системы (2), при условии, что
. Итак, решением первого уравнения системы (2), при условии, что 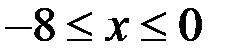 , является пара
, является пара  , или пара
, или пара  Но пара
Но пара  не удовлетворяет второму уравнению системы (2), а тогда исходная система, если
не удовлетворяет второму уравнению системы (2), а тогда исходная система, если  имеет единственное решение – это пара
имеет единственное решение – это пара 
2) Если  то система (1) принимает вид
то система (1) принимает вид

Квадратное уравнение  имеет два корня:
имеет два корня: 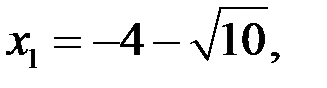
 , которые удовлетворяют условию
, которые удовлетворяют условию 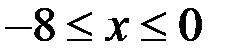 . Система (3) имеет два решения:
. Система (3) имеет два решения:  Условию задачи
Условию задачи  не удовлетворяет.
не удовлетворяет.
3) Если  то система (1) принимает вид
то система (1) принимает вид

Квадратное уравнение  имеет два корня:
имеет два корня: 
 , которые удовлетворяют условию
, которые удовлетворяют условию 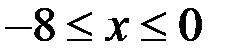 . Система (3) имеет два решения:
. Система (3) имеет два решения: 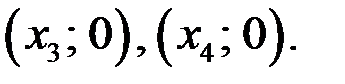 Условию задачи
Условию задачи  не удовлетворяет.
не удовлетворяет.
Ответ. 
38. Найдите все значениях параметра а, при которых имеет единственное решение система

Решение. Так как система не меняется при замене у на х и х на у, то вместе с решением  система имеет решение
система имеет решение  Тогда необходимым условием существованием единственного решения системы является выполнения условия
Тогда необходимым условием существованием единственного решения системы является выполнения условия 
Если 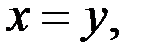 то первое неравенство системы (1) принимает вид
то первое неравенство системы (1) принимает вид

Последнее квадратное неравенство имеет единственное решение, если равен нулю дискриминант этого неравенства, то есть, если

Если  , то система (1) может иметь единственное решение.
, то система (1) может иметь единственное решение.
Если  , то система (1) принимает вид
, то система (1) принимает вид

Решением следствия исходной системы является одна пара  Поэтому система (1) имеет не более одного решения и, если эта система имеет решение, то этим решением является пара
Поэтому система (1) имеет не более одного решения и, если эта система имеет решение, то этим решением является пара  Проверкой убеждаемся, если
Проверкой убеждаемся, если  , то решением исходной системы является пара
, то решением исходной системы является пара 
Ответ.  .
.
39. Найдите все значения параметра а, при которых имеет два решение система

Решение. Если  решение системы, то и
решение системы, то и  также решение системы. Так как система не меняется при замене у на х и х на у, то вместе с каждым решением
также решение системы. Так как система не меняется при замене у на х и х на у, то вместе с каждым решением  система имеет решение
система имеет решение 
Итак, если  решение системы, то решениями являются
решение системы, то решениями являются 
Система (2) может иметь два решения, если совпадают какие-либо два решения.
1) Если 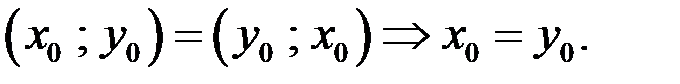
Тогда необходимым условием существования двух решений системы (1) является выполнения условия 
Если 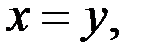 то первое уравнение системы (1) принимает вид
то первое уравнение системы (1) принимает вид

Итак, если 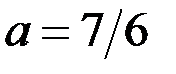 , то система (1) может иметь два решения.
, то система (1) может иметь два решения.
Определим, число решений системы (1), если 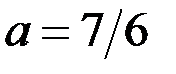 .
.
Если 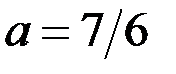 , то система (1) принимает вид
, то система (1) принимает вид

Последняя система имеет два решения 
Итак, 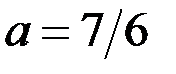 удовлетворяет условию задачи.
удовлетворяет условию задачи.
2) Если 
Тогда необходимым условием существованием двух решений системы (1) является выполнения условия 
Если  то система (1) принимает вид
то система (1) принимает вид

Последняя система, а значит и система (1), не имеет решений.
3) Имеем 
Ни при каких значениях параметра а пара  не является решением системы (1).
не является решением системы (1).
4) Если 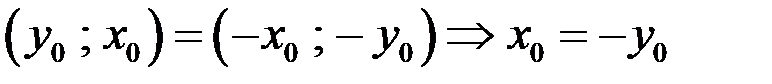 (как 1)).
(как 1)).
5) Если  (как 3)).
(как 3)).
6) Если  (как 2)).
(как 2)).
Ответ. 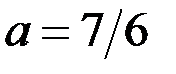 .
.
40. Найдите все значения параметра а, при которых имеет единственное решение система 
Решение. Отметим: 
1. Легко проверить, если  решение системы, то и
решение системы, то и 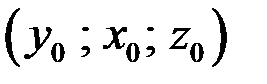 (система не меняется при замене у на х и х на у).
(система не меняется при замене у на х и х на у).
Система (1) может иметь единственное решение, если 
Если 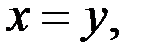 то систем (1) принимает вид
то систем (1) принимает вид
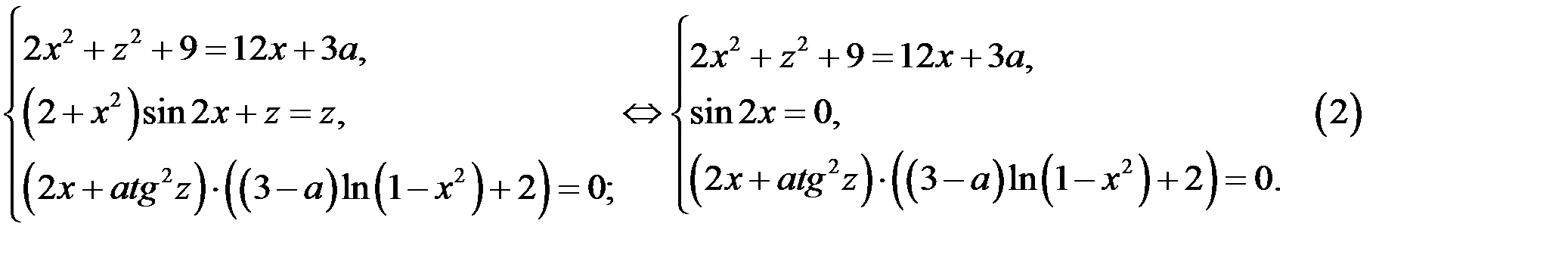
Из второго уравнения системы (2) находим, что 
Из третьего уравнения системы (2) следует:  Тогда
Тогда

Так как  то
то 
Так как  то из первого уравнения системы (2) находим: что
то из первого уравнения системы (2) находим: что  Система (2) имеет единственное решение, если имеет единственное решение уравнение
Система (2) имеет единственное решение, если имеет единственное решение уравнение  , то есть, если
, то есть, если  тогда
тогда 
Итак, тройка  является решение системы (2), если
является решение системы (2), если 
2. Если  , то система (1) принимает вид
, то система (1) принимает вид

Из третьего уравнения системы (3) следует, что 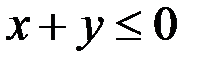 . Тогда из первого уравнения системы (3) имеем
. Тогда из первого уравнения системы (3) имеем

Проверкой убеждаемся, что тройка  является решением системы (3). Это решение единственное. Итак, если
является решением системы (3). Это решение единственное. Итак, если  , то исходная система имеет единственное решение.
, то исходная система имеет единственное решение.
Ответ.  .
.