Рассчитаем число Архимеда

Контрольная работа №1 по

Процессам и аппаратам пищевых производств

Студента 3 курса ФБО ВГТА (г. Калуга)

Специальность 260601

Картанова Андрея Игоревича

Шифр 09-741

 

 

Задача № 1.

Определить необходимую длину песколовки шириной b для осаждения из промышленных стоков примесей минерального и органического происхождения, если в ней осветляется V сточных вод, их температура t, минимальный размер улавливаемых частиц d, плотность частиц r_т. Скорость движения стоков в песколовке v. Действительную скорость осаждения принять вдвое меньше теоретической. Описать методы интенсификации процесса осаждения.

Значения V, b и v принять по предпоследней цифре шифра:

 

Предпоследняя цифра шифра
V.102, м3/с	1,0	1,4	1,8	2,2	2,6	3,0	3,4	3,8	4,0	4,4
B, м	0,3	0,35	0,4	0,45	0,5	0,55	0,6	0,65	0,7	0,75
v, м/с	1,0	1,1	1,2	1,3	1,4	1,5	1,6	1,7	1,8	1,9

 

Значения t, d и r_т принять по последней цифре шифра:

Последняя цифра шифра
t, 0С
d.106, м
rт, кг/м3

 

Решение задачи

 

Воспользуемся уравнением расхода

,

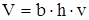где b^.h –площадь поперечного сечения потока.

Тогда

.

Здесь v - скорость движения жидкости в песколовке

b -ширина песколовки

V – расход жидкости

 

м

Определим физические свойства жидкости для t=14^оС

ρ_с=1000 кг/м³, μ_с=1,31^.10^-3 Па^.с (приложение 1)

 

Рассчитаем число Архимеда

,

,

следовательно, режим осаждения ламинарный. Для расчета скорости осаждения воспользуемся формулой Стокса

,

м/с.

Найдем действительную скорость осаждения частиц

м/с.

Находим время пребывания частиц в песколовке

c

Найдем длину песколовки

l= v^.τ=1,4^.5,72=8 м.

Рассмотрим способы интенсификации процесса осаждения.

Для ускорения процесса необходимо увеличть температуру, так как с повышением температуры согласно формуле Стокса уменьшается вязкость и увеличивается скорость осаждения частиц; а также увеличить размер осаждающихся частиц путем добавления специальных веществ - флокулянтов.

Задача № 2.

 

Определить продолжительность разделения объема V суспензии через 1 м² фильтра, если при лабораторных исследованиях в подобных условиях с 1 м² фильтра собрано фильтрата: q ₁ через t ₁, q ₂ через t ₂, q ₃ через t ₃, q ₄ через t ₄ после начала фильтрования. Привести схему рамного фильтр-пресса, описать его устройство и работу.

Значение V принять по предпоследней цифре шифра.

 

Предпоследняя цифра шрифта
V × 103, м3

 

Соответствующие значения t и q принять по последней цифре шифра.

 

Последняя цифра шрифта
q 1 × 103, м3/м2	7,5	4,6	4,6	7,6	4,6	7,6	2,3	3,6	3,7	4,6
t 1,с
q 2 × 103, м3/м2	13,7	16,8	13,7	23,0	13,7	13,6	7,1	15,1	15,0	16,8
t 2,с
q 3 × 103, м3/м2	23,0	23,0	19,8	29,2	19,8	23,0	15,1	20,9	20,9	26,2
t 3,с
q 4 × 103, м3/м2	29,2	29,2	26,2	35,3	26,2	29,2	21,0	26,9	26,9	32,2
t 4,с

 

решения задачи

 

Определение констант процесса фильтрования выполним по традиционной методике.

 

Из графика м²/с,

K – константа, учитывающая режим процесса фильтрования и физико-химические свойства осадка и жидкости, м²/с;

С – константа, характеризующая гидравлическое сопротивление фильтрованной перегородки, м³/м².

Решим основное уравнение процесса фильтрования при постоянном перепаде давления при найденных значениях констант К и С.

 

Найдем приращения удельных объемов фильтрата D q ₁, D q ₂, D q ₃, D q ₄ и приращения времени отбора известных объемов фильтрата D t ₁, D t ₂, D t ₃, D t ₄:

 

D q ₁ = q ₁ = 4,6 × 10^-3 м³/м²;

D q ₂ = q ₂ – q ₁ = (16,8 – 4,6) × 10^-3 = 12,2 × 10^-3 м³/м²;

D q ₃ = q ₃- q ₂ = (23-16,8) × 10^-3 = 6,2 × 10^-3 м³/м²;

D q ₄ = q ₄- q ₃ = (29,2 – 23) × 10^-3 = 6,2 × 10^-3 м³/м²

и

D t ₁ = t ₁ = 53 с;

D t ₂ = t ₂ - t ₁ = 195 – 53 = 142 с;

D t ₃ = t ₃ - t ₂ = 320 – 195 = 125 с;

D t ₄ = t ₄ - t ₃ = 470 – 320 = 150 с.

Для построения графической зависимости 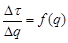вычислим отношения :

 

;

.

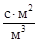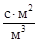
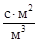
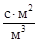Строим график зависимости 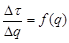(рисунок 1).

 

, тогда

,

, отсюда

м³/м², 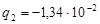м³/м².

Т.к. удельная производительность не может быть отрицательной, то q = q ₁ = 1,86 × 10^-4 м³/м².

При постоянной движущей силе процесса фильтрования объем фильтрата V, проходящий через 1 м² фильтрованной поверхности за время t и время процесса фильтрования связаны уравнением

.

Подставив в него найденные константы процесса фильтрования К и С, определим продолжительность процесса фильтрования

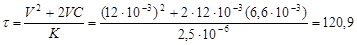с = = 2 мин 9 с.

Фильтр-пресс состоит из ряда чередующихся друг с другом плит и полых рам. Между рамами и плитами помещают фильтровальный пористый материал, пропускающий жидкость (фильтрат) и задерживающий твердые частицы, образующие на его поверхности осадок. После заполнения пространства рамы осадком фильтр разбирают, осадок удаляют, заменяют фильтровальный материал и вновь плотно сжимают плиты с рамами.

На рисунке 3 изображены плиты и рамы фильтр-пресса, а на рисунке 2 – схема работы плиточно-рамного фильтр-пресса [2].

1- средний канал; 5 – рама;

2,9 – каналы; 6 – канал для отвода фильтрата;

3 – пространство между плитами; 7 – кран;

4- плиты; 8 – боковой канал.

 

Рисунок 2 – Схема работы плиточно-рамного фильтр-процесса

 

Рисунок 3 –Схема работы плиточно – рамнго фильтр – пресса: А – стадия фильтрования, В – стадия промывки; 1 – средний канал; 2, 9 – каналы; 3 – пространство между плитами; 4 – плиты; 5 – рама; 6 – канал для отвода фильтрата; 7 – кран; 8 – боковой канал

А – плита, Б – рама;

1 – гладкая поверхность плиты;

2 – желобок;

3 – фильтровальная перегородка;

4 – канал для удаления фильтрата и промывной жидкости;

5 – отверстия для прохода суспензии;

6 – отверстия для прохода промывной жидкости.

 

Рисунок 3 – Плиты и рамы фильтр-пресса

Задача № 3.

Определить мощность электродвигателя мешалки диаметром d для перемешивания суспензии слоем H, если плотность жидкой фазы r, а ее вязкость m. Объемное содержание твердых частиц в суспензии x, плотность твердых частиц r_ч. Окружная скорость лопастей мешалки w.

 

Значения d, H, w, x и тип мешалки принять по предпоследней цифре шифра.

 

Предпоследняя цифра шифра:
d, м	1,00	0,60	0,80	0,70	0,30	0,60	0,95	0,40	0,25	0,50
H, м	2,0	1,7	2,2	1,4	1,1	2,0	1,9	1,2	1,0	1,8
w, м/с	4,0	5,2	6,3	3,5	11,5	7,1	2,9	8,0	12,5	7,9
x, % об.
Тип мешалки	лопастная	пропеллерная	турбинная	лопастная	пропеллерная	турбинная	лопастная	турбинная	пропеллерная	турбинная

 

Значения r, m и r_ч принять по последней цифре шифра.

 

Последняя цифра шифра
r, кг/м3
m, Па×с	0,025	0,040	0,065	0,050	0,075	0,080	0,090	0,100	0,125	0,085
rч,кг/м3

 

Пример решения задачи

 

Суспензией называется жидкая неоднородная система, состоящая из жидкой фазы и равномерно распределенной в ней твердой фазы.

Определим плотность и вязкость суспензии [1].

Плотность

,

где x = 9 % (0,09) – объемное содержание твердых частиц в суспензии; r _тв = r _ч = 1700 кг/м³ – плотность твердых частиц; r _ж = r = 1080 кг/м³ – плотность жидкой фазы.

Тогда5

кг/м³.

Т.к. объемная концентрация твердой фазы в суспензии меньше 10 %, то динамическую вязкость суспензии определим по формуле Бачинского А.И. [1]

,

где = m = 0,090 Па×с – вязкость жидкой фазы.

Тогда

Па×с.

Определим скорость вращения мешалки из выражения

,

где w – окружная скорость лопастей пропеллерной мешалки, м/с; n – частота вращения мешалки, 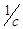; d – диаметр мешалки;

w = 5,2 м/с (по условию).

Тогда

.

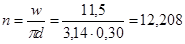
Для пропеллерных мешалок в аппаратах без перегородок диаметр аппарата D = 3 d = 0,30×3=0,9 м.

Т.к. , то мешалка отличается от геометрически подобных мешалок (для которых проведены исследования и в литературе представлены значения коэффициентов мощности С) и следует определить поправку по формуле [9]

.

Рассчитаем модифицированный критерий Рейнольдса:

.

По графику зависимости коэффициента сопротивления С от критерия Рейнольдса [1] для пропеллерной мешалки в аппарате без перегородок (кривая 6) С = 0,30 (приложение 2).

Мощность на перемешивание в рабочий период

N_D =0,3*0,3⁵*12,208³*1082,741*1,127=1618,488 Вт = 1,1618488 кВт

Лопасти пропеллерных мешалок изогнуты по профилю судового винта. Пропеллер обычно имеет три лопасти. Диаметр пропеллера равен 0,25 – 0,3 диаметра аппарата. Скорость вращения пропеллера составляет 160 – 1000 об/мин.

Пропеллерные мешалки создают интенсивные осевые потоки, способствующие лучшему перемешиванию суспензии.

 

 

Задача 4.

 

Определить коэффициент теплоотдачи от стенки трубки конденсатора к охлаждающей воде, если средняя по длине температура стенки t_с, внутренний диаметр трубки d, температура воды на входе и выходе из трубки равны соответственно t₁ и t₂ и средняя скорость воды v.

Определить также количество передаваемой теплоты и длину трубки.

 

Значения t_с, t₁ и t₂ принять по предпоследней цифре шифра.

 

Предпоследняя цифра шифра
tс, оС
t1, оС	0,025	0,040	0,065	0,050	0,075	0,080	0,090	0,100	0,125	0,085
t2 оС

 

Значения d и υ принять по последней цифре шифра.

 

Предпоследняя цифра шифра
d∙103, м
υ, м/с	1,1	1,0	0,9	0,8	0,7	0,6	0,5	0,4	0,3	0,2

 

Пример решения задачи.

 

Определим среднюю температуру воды

^оС

По приложению 1 [2] определим теплофизические свойства воды

при t_ср= 20 ^оС

ρ=998 кг/м³ плотность воды

μ= 1·10^-3 Па·с динамический коэффициент вязкости

λ=0,599 Вт/(м·К) коэффициент теплопроводности

с=4190 Дж/(кг·К) коэффициент теплоемкости

Рr= 7,02 число Прандтля

Определим режим течения, критерий Рейнольдса равен

Т.к. Re>10000, то режим течения турбулентный и критериальное уравнение для расчета критерия Нуссельта имеет вид

,

где Pr_ст=3,26 - число Прандтля, определенное при t_с=55 ^оС

Nu=0,021·23952^0,8·7,02^0,43(7,02/3,26)^0,25=187,5

Коэффициент теплоотдачи от стенки к воде

Вт/(м²·К)

Расход воды

кг/с

Количество отдаваемого тепла с учетом потерь в окружающую среду

0,752·4190·(32-8)·1,04=78646 Вт

χ=1,03-1,05 – коэффициент, учитывающий потери тепла в окружающую среду.

Удельный тепловой поток

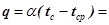2808·(55-20)=98280 Вт/м²

Длина трубки

м

 

Список литературы

1. Павлов К.Ф., Романков П.Г., Носков А.А. Примеры и задачи по курсу процессов и аппаратов химической технологии. – Л.: Химия, 2004.

2. Практикум по процессам и аппаратам пищевых производств: Учеб пособие/ А.В. Логинов, Л.Н. Ананьева, Ю.В. Красовицкий, С.В. Энтин; Воронеж. Гос. Технол. Акад. Воронеж, 2003.336 с.

3. Асмолова Е.В. Процессы и аппараты пищевых производств (руководство по изучению курса) [Текст]: учеб. пособие / Е.В. Асмолова, Ю.В. Красовицкий, А.В. Логинов; Воронеж. гос. технол. акад. – Воронеж: ВГТА, 2007 – 308 с.