Гранью в плоском представлении графа называется часть плоскости, ограниченная простым циклом и не содержащая внутри себя других циклов.
Простой цикл, ограничивающий грань, называется границей грани.
Две грани называются соседними, если их границы имеют хотя бы одно общее ребро.
задача 1. Приведите пример правильно нарисованного связного плоского графа для которого формула В - Р + Г = 2, не верна. (В, Р, Г - число вершин, ребер и граней графа)
Мостом в графе называется ребро (AB), при удалении которого вершины A и B становятся несвязными.
Перегородкой в графе называется мост, соединяющий два цикла.
задача 2. Докажите, что для любого правильно нарисованного связного плоского графа без перегородок верна формула В - Р + Г =2.
Плоский граф называется максимально плоским, если при добавлении к нему любого ребра (если этого ребра ранее не было) он становится не плоским.
Граф называется триангулированным, если, в его плоском представлении каждая грань имеет 3 вершины.
Операция добавления новых ребер, в результате которой в плоском представлении каждая грань имеет ровно 3 вершины, называется триангуляцией графа.
задача 3. Всегда ли максимально плоский граф является триангулированным?
задача 4. Докажите, что существует ровно один триангулированный граф с четырьмя вершинами и ровно один - с пятью вершинами.
задача 5. Опровергните утверждение: триангулированные графы с одним и тем же числом вершин совпадают. Верно ли это утверждение если число вершин в графе равно 7?
задача 6. Докажите, что в плоском представлении триангулированного графа с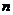 
вершинами число треугольных граней равно 
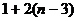, если бесконечную грань не учитывать.
задача 7. (Лемма Шпернера). Вершины треугольника помечены цифрами 0, 1, 2. Этот треугольник разбит на несколько треугольников таким образом, что никакая вершина одного треугольника не лежит на стороне другого. Вершинам исходного треугольника оставлены старые пометки, а дополнительные вершины получают номера 0, 1, 2, причем любая вершина на стороне исходного треугольника должна быть помечена одной из пометок вершин этой стороны. Докажите, что число треугольников разбиения, помеченных цифрами 0,1,2 нечетно.
задача 8. Можно ли нарисовать квадрат и его диагонали не отрывая карандаша от бумаги и не проводя никакой линии дважды?
Эйлеровым путем (циклом) в графе называется путь (цикл), содержащий все ребра графа.
задача 9. Докажите, что если граф обладает эйлеровым путем с концами A и B (A не совпадает с B), то A и B - единственные нечетные вершины этого графа.
задача 10. Докажите, что если граф связный и A и B - единственные его нечетные вершины, то этот граф обладает эйлеровым путем с концами A и B.
задача 11. (Задача Эйлера о кенигсбергских мостах). На реке 2 острова – Большой и Малый. Большой соединен с каждым берегом двумя мостами, а также соединен одним мостом с Малым. Малый, помимо Большого, соединен с каждым берегом одним мостом. Доказать, что, откуда ни начни обход, нельзя обойти все мосты, пройдя каждый мост ровно один раз.
Граф, обладающий эйлеровым циклом, называется эйлеровым графом.
задача 12. Граф является эйлеровым тогда и только тогда, когда все его вершины четные.
задача 13. Имеется группа островов, соединенных мостами так, что от каждого острова можно добраться до любого другого. Турист обошел все острова, пройдя по каждому мосту ровно один раз. На острове Троекратном он побывал трижды. Сколько мостов ведет с Троекратного, если турист а) не снего начал и не на нем закончил? б) с него начал, но не на нем закончил? в) с него начал и на нем закончил?
задача 14. Дан кусок проволоки длиной 120 см. Какое наименьшее число раз придется ломать проволоку, чтобы изготовить из нее каркас куба с ребром 10 см?
задача 15. Докажите, что если связный граф имеет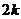 
нечетных вершин, то найдется семейство из 
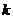путей, которые в совокупности содержат все ребра графа в точности по одному разу.
задача 16. Докажите, что если граф связный, то можно построить цикличный маршрут, содержащий все ребра графа ровно два раза, по одному в каждом направлении.
Указание: покажите, что такой цикличный маршрут можно построить воспользовавшись правилом Тарри - выходим из произвольной вершины в произвольном направлении. Ребро, по которому попали в вершину используется для выхода только тогда, когда оно остается единственным выходом из этой вершины.
задача 17. Докажите, что не для всякого связного графа найдется цикличный маршрут, содержащий все его ребра ровно три раза.