Информационное неравенство Рао-Крамера

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Лекция 2

Нижняя граница для дисперсии несмещенной оценки

Информационное неравенство Рао-Крамера

Оказывается, никаким выбором оценочной функции невозможно сделать дисперсию ошибки меньше, чем некоторое определенное значение.

Пусть 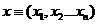— результаты n наблюдений (не обязательно независимых), являющиеся конкретными значениями многомерной случайной величины x º (x₁, x₂…x_n). Закон распределения 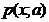известен с точностью до параметра a (будем считать 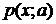плотностью распределения, если 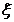непрерывна, и вероятностью, если x дискретна). Мы рассматриваем различные несмещенные оценки 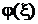для 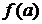(может быть, нам нужна оценка не для а, а для а ²= 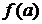или для sin a = 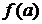; функция 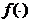известна, но значение параметра a неизвестно). Как обычно, рассматривая статистические задачи, мы отвлекаемся от конкретного значения 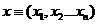, считая его одной из возможных реализаций случайной величины ξ ≡ (ξ₁, ξ₂…ξ_n), а оценку 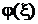рассматриваем как случайную величину.

Теорема. Для любой оценки 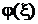, несмещенно оценивающей 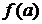, при условиях, оговариваемых ниже, справедливо неравенство:

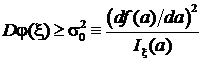, (1)

где обозначено

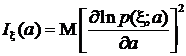= . (2)

Т. е. дисперсия несмещенной оценки не может быть меньше величины 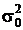, которая определяется правой частью неравенства и которую можно вычислить заранее, если известен закон распределения. Условия, при которых справедливо это неравенство, выпишем после проведения выкладок, из которых будет ясно, что именно нужно потребовать.

Обозначим через 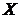множество тех значений x, при которых 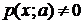, т. е. 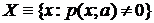. условие несмещенности

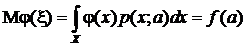(3)

продифференцируем по a. Учитывая, что 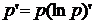, получим

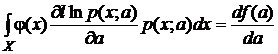. (4)

Здесь имеются в виду многомерные интегралы. Продифференцируем по a условие

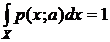. (5)

Учтем, что 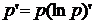. Затем, умножив результат на 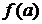, получим

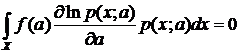. (6)

Вычтем из (4) равенство (6):

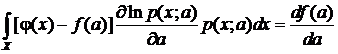. (6а)

Введем обозначения

,

.

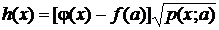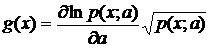Возведя (6а) в квадрат, получим:

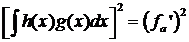. (7)

Применим к левой части (7) неравенство Коши – Буняковского – Шварца:

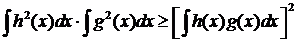
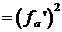(8)

Получим:

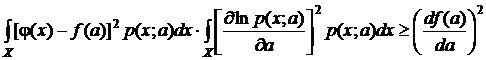. (9)

Здесь первый множитель есть 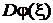, а второй 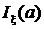, так что (9) совпадает с (1).

Условия, которые нужно наложить на 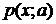для справедливости (1):

1) множество 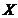не должно зависеть от a, иначе нельзя дифференцирование в (3) и (5) внести под знак интеграла;

2) функция 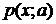должна быть дифференцируемой по a;

3) интегралы в (9) должны существовать.

Следствие. Если оценивается само значение параметра a, т. е. 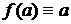, то

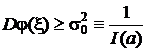. (10)

3.2. Информация Фишера

Величина 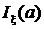в формуле (2) называется информацией Фишера, содержащейся в выборке x относительно параметра a.

Свойства информации.

1. О вычислении.

Справедлива следующая формула:

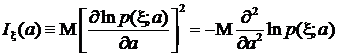. (11)

Действительно,

,

.

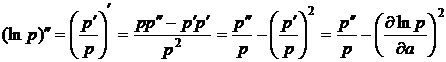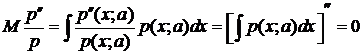2. Аддитивность информации Фишера.

Информация, содержащаяся в n независимых наблюдениях, равна сумме информаций, содержащихся в отдельных наблюдениях.

Действительно, пусть ξ = (ξ₁, ξ₂ … ξ _n), где 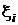— независимы и распределены по закону 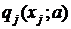. Тогда, если обозначено x = (x ₁, x ₂… x_n), то 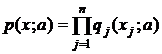. Вычислим информацию в наблюдениях :

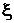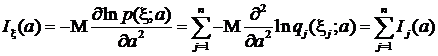, (12)

где 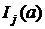— информация, содержащаяся в одном наблюдении 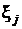. Если все наблюдения распределены одинаково, т. е. 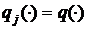для всех 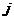(это означает, что мы имеем дело с выборкой (ξ₁, ξ₂ … ξ _n)), то

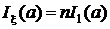, (13)

где 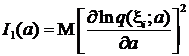— информация в одном наблюдении.

Следствие. Если ξ = (ξ₁, ξ₂ … ξ _n) — выборка, то из (10) и (13) следует:

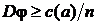. (14)

Это означает, что в условиях, в которых справедливо неравенство Рао – Крамера, дисперсию оценки нельзя сделать убывающей быстрее, чем .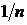

Замечания.

1. Об обобщениях неравенства (1).

Неравенство Рао – Крамера обобщалось в различных направлениях — снимались ограничения, в основном, первое ограничение. Различные обобщения, в том числе на многомерный случай, можно найти в книгах [5], [6].

2. Об использовании неравенства.

С помощью (1) можно выносить суждения о качестве имеющихся оценок. далеко не всегда удается найти оптимальную оценку, т.к. или она не существует (неравенство не утверждает, что существует оптимальная оценка), или, если существует, то трудно реализуема в вычислительном отношении.

Пусть из каких-либо соображений построена оценка j. Как оценить ее качество? Если 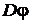близка к 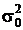, это означает, что оценка «хорошая». Если же нет, то с некоторой осторожностью можно считать, что оценка j «плохая», поскольку известно, что при широких условиях существуют оценки с дисперсией, асимптотически (с ростом n) приближающейся к значению 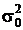(см. раздел 5.2).