Статистическими называют гипотезы о типе неизвестного распределения или о параметрах известных распределений. С проверкой гипотезы о типе распределения мы уже знакомились в теме анализа эмпирических распределений, где рассматривалось использование критерия 
дляоценки соответствия эмпирического распределения тому или иному типу теоретических распределений.
Выдвигаемая для проверки гипотеза называется основной или нулевой и обозначается 
, гипотеза, противоречащая основной, называется альтернативной или конкурирующей - 
. Например,выдвигается гипотеза, что генеральная средняя равна 100, что записывается = 100, тогда альтернативная гипотеза - генеральная средняя не равна 100: 
.
Проверка правильностинулевой гипотезы сопряжена с возможностью допустить ошибки двух родов. Ошибка первого рода состоит в том, что нулевая гипотеза будет отвергнута, при том, что она верна.
Ошибка второго рода - будет принята нулевая гипотеза, при том, что на самом деле она ошибочна.
Вероятность допустить ошибку первого рода обозначают 
и ее величина называется уровнем значимости принятия нулевой гипотезы. Если, например, =0,05 - это означает, что в пяти случаях из ста имеется риск отвергнуть правильную нулевую гипотезу, т.е. допустить ошибку первого рода.
Для проверки нулевой гипотезы используются специальные случайные величины (критерии), закон распределения который известен. Наиболее распространенными в практическом использовании являются: t - статистика, F - критерий, z - статистика критерий-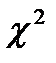 
и др.
Для проверки нулевой гипотезы все множество возможных значений критерия разбивается на две непересекающиеся области. Одна область содержит значения критерия, при которых нулевая гипотеза не отвергается, другая - значения, при которых нулевую гипотезу следует отвергнуть. Эта область значений критерия называется критической. Точки (значения), отделяющие критическую область от области принятия гипотезы, называются критическими, границами критической области. Проверка гипотезы реализуется следующим образом: по выборочным данным рассчитывается фактическое значение критерия, если это значение попадает в критическую область, то нулевая гипотеза отвергается, в противном случае - гипотеза принимается.Значения критериев табулированы. Табличные значения критериев – это и есть те критические точки, которые отделяют область допустимых значений критерия от области значений, попадание в которую будет означать необходимость отвергнуть нулевую гипотезу.
В практических исследованиях наиболее часто возникает потребность в оценке двух видов гипотез о средних величинах:
1) гипотеза о равенстве генеральной средней какому-либо конкретному числу, например, установленному нормативу;
2) гипотеза о равенстве средних значений той или иной характеристики в двух совокупностях.
Проверка гипотез осуществляется по данным выборочных наблюдений.
При оценке первой гипотезы (о равенстве генеральной средней какому-либо конкретному числу)нулевая гипотеза формулируется:
, т.е. среднее значение признака в совокупности равно, соответственно альтернативная гипотеза -.
Например, по стандарту внутренний диаметр производимых шин должен быть равен 575 мм. Для оценки фактического диаметра в выборку отобрано 35 шин. Средний диаметр по выборке - 575,2 мм., среднее квадратическое отклонение составило S=1,8 мм. Нулевая гипотеза запишется:, альтернативная -..
Примем уровень значимости =0,05, тогда:
и критическая область будет задаваться неравенством: 
. В качестве критерия может быть использовано нормированное отклонение выборочной средней от установленного норматива, t - статистика:
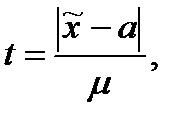
(5.7)
где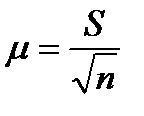 
- средняя ошибка выборки.
Расчетное значение критерия по данным примера составит:
).
Поскольку объем выборки более 30 единиц, для нахождения табличного значения критерия можно обратиться к таблице интеграла вероятностей Лапласа.При установленном уровне значимости t = 1,96. Это критическое значение статистики, при условии превышения которого, нулевая гипотеза должна быть отвергнута. Поскольку 
, нулевую гипотезу о равенстве генеральной средней установленному нормативу следует принять.Расхождение между выборочной средней и нормативом - результат влияния случайных факторов,т.е. фактический средний размер диаметра шин равен стандарту, отклонения, наблюдаемые в выборке, находятся в рамках статистической погрешности.
Проверка второй гипотезы - о равенстве средних в двух совокупностях - часто используется при оценке влияния каких-либофакторов (мероприятий) на изменение средней величины конкретного показателя, например: повлияли ли мероприятия по совершенствованию организации труда на уровень его производительности; значимо ли изменился средний объем продаж после проведения рекламной компании; повлияло ли введение налоговых льгот на уровень инновационной активности организаций; повлияло ли внедрение нового оборудования на экономию сырья и т.п. Нулевая гипотеза формулируется:
. Суть гипотезы - среднее значение осталась неизменным, что говорит об отсутствии влияния анализируемого фактора или мероприятия.
Для оценки данного вида гипотез используются выборочные данные, полученные до и после проведения мероприятия или начала действия какого-либо фактора: объемы выборок принято обозначать 
и 
, выборочные средние - 
и 
, выборочные дисперсии соответственно - 
и 
. Для оценки такого вида гипотез t - статистика рассчитывается следующим образом:
(5.8)
где - среднеквадратическая ошибка разности двух
выборочных средних. Величина дисперсии определяется как средняя взвешенная из дисперсий двух выборок, в качестве весов используется число степеней свободы (n - 1), итоговая формула:
. (5.9)
Табличное значение критерия, как и при проверке гипотез первого типа, находится, исходя из принятого уровня значимости по таблице интеграла вероятностей Лапласа, если использованы выборки большого объема, или по таблице t - распределения Стьюдента, если выборки малого объема. Результаты оценки гипотезы формулируются следующим образом: если , то принимается нулевая гипотеза о равенстве средних величин, т.е. расхождение между средними величинами признается несущественным, обусловленным случайными факторами, а, следовательно, мероприятия или оцениваемый фактор не отразились на среднем значении показателя.
Если то нулевая гипотеза отвергается и принимается альтернативная, состоящая в том, что средние значения не равны, т.е. различие в значениях обусловлено не случайными факторами, а мероприятиями (факторами), влияние которых оценивалось.