Парная корреляционная зависимость – зависимость между двумя признаками, один из которых – признак-результат (зависимая переменная, следствие, отклик), второй – признак-фактор (независимая переменная, причина, аргумент). Если оценивается влияние на зависимую переменную двух и более факторов, такая зависимость называется множественной.
Как отмечалось выше, оценка наличия или отсутствия статистически значимой корреляционной зависимости производится на основе показателей корреляции. Слово корреляция означает соответствие, соотношение. По существу, проводя оценку связей между признаками на основе КРА, мы оцениваем,насколько вариация значений результативного признака соответствует вариации значений признака-фактора.
Учитывая сложность социально-экономических явлений, стоит предположить, что парных связей, в принципе, не существует. В реальности на результат всегда воздействует множество факторов. Изучение влияния лишь одного фактора на признак-результат связано с практической потребностью оценить степень влияния именно данного,конкретного фактора, либо среди множества факторов, влияющих на анализируемый признак-результат, выделяется один доминирующий, поэтому внимание концентрируется на оценке влияния именно этого фактора.
Показатели корреляции характеризуют степень тесноты корреляционной зависимости. К этим показателям относятся:
Ø Коэффициент корреляции.
Ø Коэффициент детерминации.
Ø Корреляционное отношение (эмпирическое и теоретическое).
Ø Индекс корреляции.
Исторически первым показателем тесноты связи был парный линейный коэффициент корреляции, предложенный К. Пирсоном. Он основан на показателе ковариации, который представляет собой среднее значение произведения отклонений индивидуальных значений результативного и факторного признаков от соответствующих средних значений. Показатель ковариации - cov(y,x) - оценивает совместное изменение двух признаков, результата и фактора:
(6.1)
где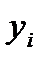 
- значение признака-результата у i-й единицы совокупности; 
- значение признака-фактора у i-й единицы совокупности; 
- среднее значение признака-результата; 
- среднее значение признака-фактора.
Показатель ковариации содержательно сложно интерпретировать, поскольку он не имеет пределов изменения. Нормированное значение показателя ковариации – это и есть показатель парной корреляции Пирсона:
, (6.2)
или после ряда преобразований:
, (6.3)
где 
- стандартное отклонение признака-результата; 
- стандартное отклонение признака-фактора.
Достоинством коэффициента корреляции является то, что он имеет пределы изменения, следовательно, его величина легко может быть интерпретирована. Значения показателя изменяются от -1 до +1. Знак коэффициента корреляции указывает на прямую (знак "+"), либо обратную (знак "-") зависимость. Близость коэффициента к нулю свидетельствует об отсутствии корреляционной зависимости. Близость к единице – о тесной корреляционной зависимости. Для интерпретации конкретных значений коэффициента корреляции, как правило, используется шкала Чеддока:
- связь слабая (практически отсутствует);
- связь умеренная;
- связь заметная;
- высокая (тесная);
- весьма высокая (весьма тесная).
Так, например, при оценке зависимости затрат организаций пищевой отрасли от объема выпуска,коэффициент корреляции составил: 
= 0,87. Следовательно, зависимость между анализируемыми показателями в конкретных условиях может оцениваться как прямая и тесная.Изучая зависимость между уровнем среднедушевых денежных доходов населения и величиной валового регионального продукта (ВРП) на душу населения в регионах России (по данным 2013 года), получен коэффициент корреляции = 0,777, что также подтверждает наличие прямой и тесной зависимости.
Парный коэффициент корреляции – симметричный показатель, т.е. 
. Это означает, что высокое значение коэффициента корреляции не свидетельствует о наличии причинно-следственной связи, а говорит лишь о наличии параллельной вариации признаков (показателей). Наличие причинно-следственной связи обосновывается теоретическим анализом изучаемого объекта, исходя из положений экономической теории.
Расчет коэффициента корреляции, как и большинства статистических показателей, рассчитываемых по ограниченному объему совокупности, сопровождается оценкой его статистической значимости (существенности). Необходимо подтвердить, что полученное значение коэффициента – не результат действия случайных факторов. Для оценкистатистической значимости рассчитывается t-статистика, как отношение оцениваемой характеристики (в данном случае - r) к ее стандартной ошибке (
):
(6.4)
Иными словами, осуществляется проверка гипотезы об отсутствии корреляционной зависимости между изучаемыми переменными, т.е. предполагается, что коэффициент корреляции в генеральной совокупности равен нулю (
):.
При большом объеме выборки и при условии, что распределение единиц в генеральной совокупности соответствует нормальному, распределение линейного коэффициента корреляции также подчинено нормальному закону распределения. Дисперсия коэффициента корреляции в этом случае будет равна:
(6.5)
следовательно, средняя квадратическая ошибка коэффициента корреляции может быть рассчитана следующим образом:
(6.6)
Расчетное значение t-статистики (см. 6.4) сравнивается с табличным значением, которое находится, исходя из принятого исследователем уровня значимости 
. Гипотеза об отсутствии связи принимается, если 
, в противном случае нулевая гипотеза отклоняется и принимается альтернативная - о статистической значимости коэффициента корреляции, т.е. о наличии связи между изучаемыми признаками.
Продолжая анализировать зависимость между уровнем среднедушевых денежных доходов населения и величиной валового регионального продукта на душу населения в регионах России, рассчитаем t-статистику для оценки статистической значимости коэффициента корреляции (n=79 - число регионов после исключения выбросов):
Табличное значение, соответствующее уровню значимости 0,05, - 1,96. Поскольку 
(
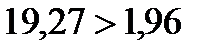), то величина коэффициента корреляции признается статистически значимой, т.е. сформированной под влиянием не случайных факторов.
Если исследование проводится по данным малой выборки, то при условии справедливости нулевой гипотезы, распределение t-статистики соответствует закону распределения вероятностей Стьюдента с n-2 степенями свободы, следовательно, табличное значение t-статистики находится, исходя из принятого аналитиком уровня значимости нулевой гипотезы и числа степеней свободы. Фактическое значение t-статистики рассчитывается также по формуле 6.4, однако особенность имеет формула расчета средней квадратической ошибки коэффициента корреляции:
(6.7)
следовательно:
(6.8)
Если расчетное (фактическое) значение t - статистики окажется больше табличного (
), то гипотеза об отсутствии связи должна быть отвергнута (с вероятностью ошибки 
=1- принятый уровень вероятности) и принята альтернативная гипотеза о значимости полученного коэффициента корреляции, т.е. о наличии зависимости между изучаемыми признаками.
Квадрат коэффициента корреляции (r2) – это коэффициент детерминации. Он характеризует, какой процент вариации результативного признака можно объяснить вариацией признака - фактора.
Продолжая рассматривать зависимость между уровнем среднедушевых денежных доходов населения и величиной валового регионального продукта на душу населения, получаем значение коэффициента детерминации r2 = 0,61. Таким образом, лишь 61 процент вариации среднедушевых денежных доходов населения в регионах России можно объяснить вариацией величины валового регионального продукта. Более глубоко сутькоэффициента детерминации станет понятна при рассмотрении корреляционного отношения.
Коэффициент корреляции, в большей степени, пригоден для оценки линейной зависимости между изучаемыми признаками. Если связь нелинейная, то следует отдать предпочтение универсальному показателю, который называется корреляционное отношение (
).
Эмпирическое корреляционное отношение рассчитывается по данным аналитической группировки (см. Лекция 4, формула 4.9), как отношение межгрупповой дисперсии (
) к общей (
):
. (6.9)
Напомним, что межгрупповая дисперсия оценивает ту часть вариации результативного признака, которая обусловлена вариацией признака - фактора, положенного в основу группировки. Общая дисперсия - это оценка вариации зависимой переменной, обусловленной всеми факторами, на нее влияющими.
Исходя из правила сложения дисперсий (общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий), корреляционное отношение оценивает долю межгрупповой дисперсии в общей. Межгрупповая дисперсия - это объясненная часть дисперсии (вариации) признака - результата. Таким образом, корреляционное отношение характеризует долю объясненной дисперсии (вариации) в общей дисперсии (вариации)зависимой переменной.
Теоретическоекорреляционное отношение рассчитывается по результатам регрессионного анализа. Регрессионный анализ (подробно будет рассматриваться ниже) предполагает построение уравнения регрессии, математически описывающего закономерность изменения условного среднего значения признака – результата под влиянием изменения признака - фактора. Используя фактические значения зависимой переменной, результаты оценки зависимой переменной на основе уравнения регрессии и разность между ними (остатки), можно так же рассчитать три вида дисперсий:
- общую дисперсию, характеризующую вариацию признака - результата под влиянием вариации всех факторов, оказывающих воздействие на результат;
- факторную дисперсию, которая оценивает ту часть вариации признака -результата, которая обусловлена фактором, учтенным в уравнении регрессии. Факторную дисперсию называют объясненной частью общей дисперсии (аналог межгрупповой дисперсии в терминах аналитической группировки);
- остаточную дисперсию, характеризующую ту часть вариации результата, которая вызвана вариацией факторов, не включенных в уравнение регрессии. Остаточную дисперсию принято называть необъясненной частью общей дисперсии признака - результата (аналог внутригрупповой дисперсии).
Приведем формулы расчета дисперсий.
Общая дисперсия:
(6.10)
где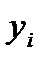 
- фактическое значение признака - результата у i-й единицы совокупности; 
- среднее значение признака - результата; n–объем совокупности.
Факторная дисперсия:
(6.11)
где 
- теоретическое значение признака - результата у i-й единицы совокупности, т.е. значение, полученное по уравнению регрессии.
Остаточная дисперсия:
(6.12)
Разность между фактическими и теоретическими значениями признака – результата называется остатками. Она характеризует величину ошибки оценивания: на сколько теоретическая величина отличается от фактических значений зависимой переменной.
Правило сложения дисперсий в терминах регрессионного анализа формулируется следующим образом: общая дисперсия признака-результата есть сумма факторной и остаточной дисперсий:
(6.13)
Формула расчета теоретического корреляционного отношения: 
. (6.14)
Корреляционное отношение изменяется так же, как и коэффициент корреляции, от нуля до единицы (но не может иметь отрицательного значения), содержательно интерпретируется аналогично коэффициенту корреляции.
Квадрат корреляционного отношения (
) - это коэффициент детерминации. Коэффициент детерминации - важный аналитический показатель, характеризующий долю факторной дисперсии в общей дисперсии результативного признака, т.е. долю вариации зависимой переменной, объясняемой вариациейфактора, включенного в уравнение регрессии.
Продолжая цифровой пример: 
=47569992, 
= 29116226,
, а = 0,612. Таким образом, величина теоретического корреляционного отношения мало отличается от значения линейного коэффициента корреляции (как и значения коэффициентов детерминации), что говорит о правомерности использования линейной зависимости при описании связи между уровнем среднедушевых денежных доходов населения и величиной валового регионального продукта на душу населения в регионах России.
Величина коэффициента детерминации реагирует на число факторов в уравнении регрессии. Поэтому для ответа на вопрос, какую часть дисперсии результативного признака удается объяснить в каждом конкретном случае, исходят из величины скорректированного коэффициента детерминации. Корректировка коэффициента осуществляется с учетом потери числа степеней свободы, т.е. с учетом числа рассчитываемых в уравнении параметров:
, (6.15)
где 
- коэффициента детерминации, скорректированный с учетом числа степеней свободы (n-k-1); 
- в скобке учтена величина не скорректированного коэффициента детерминации; n – объем изучаемой совокупности; k – число факторов, включенных в анализ.
Оценка корреляционной зависимости может быть дана и на основе индекса корреляции (
- «ро»), который рассчитывается с учетом величины остаточной дисперсии по следующей формуле:
. (6.16)
Суть данного показателя вытекает из правила сложения дисперсий. - аналог коэффициента корреляции, а 
- аналог коэффициента детерминации.