Применение метода Фурье для уравнения Лапласа рассмотрим на конкретных примерах.
Задача 1. Внутренняя задача Дирихле для прямоугольника:
в области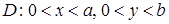 
найти такое решение уравнения Лапласа
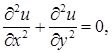
которое на контуре принимает заданные значения:
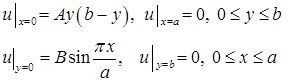
Решение. Ищем решение tв виде
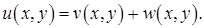
Здесь функция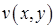 
есть решение задачи (с однородностью по 
)
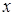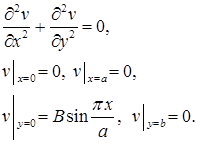(1)
Функция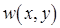 
– решение задачи (с однородностью по 
)
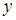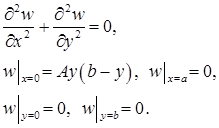(2)
А) Решение 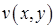задачи (1) ищем в виде
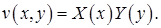
После подстановки в уравнение и разделения переменных получаем
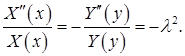
Для функции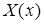 
получили знакомую задачу Штурма-Лиувилля: найти нетривиальные решения краевой задачи
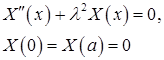
и значения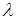 
, при которых эти решения существуют. Для этой задачи
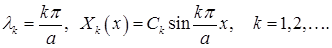
Функции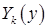 
, соответствующие собственным значениям 
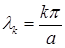, определяются из уравнения
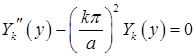
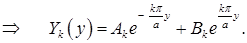
Однородное краевое условие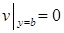 
приводит к соотношению
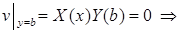
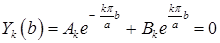
откуда находим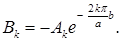 
Тогда
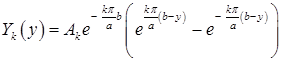
Заменим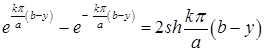 
и введем новую постоянную 
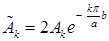. Получим
.
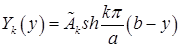Теперь можем записать функции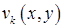 
:
.
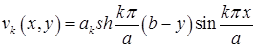Здесь обозначено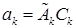 
.
Осталось составить ряд
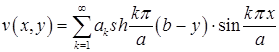(3)
и подобрать коэффициенты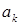 
так, чтобы удовлетворялось неоднородное краевое условие 
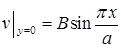. Получаем соотношение
.
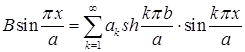Значит,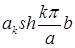 
– это коэффициенты разложения функции 
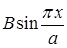в ряд Фурье по синусам на 
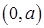. Вычислим
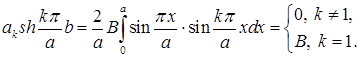
Получаем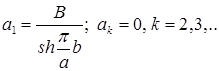 
.
И в решении (3) остается только одно слагаемое
.
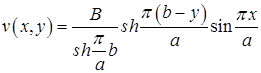Б) Решение задачи (2) также ищем методом Фурье в виде
.
Но здесь задачу Штурма – Лиувилля надо получить для функции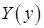 
(однородность краевых условий по 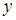). Поэтому после подстановки в уравнение, разделяя переменные, запишем
.
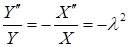Решением задачи
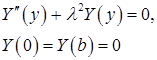
являются собственные функции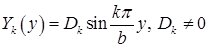 
; собственные значения суть 
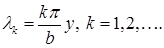Для определения функций 
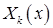получаем уравнение
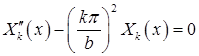
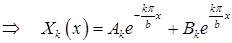
Однородное условие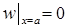 
приводит к соотношению
.
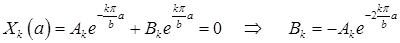Тогда
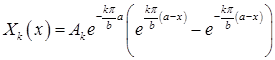
После введения новой постоянной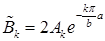 
можем записать
.
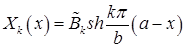Значит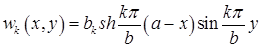 
, 
.
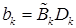Составим ряд
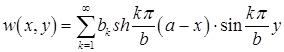(4)
Определим коэффициенты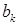 
из краевого условия 
:
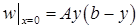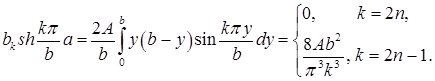
то есть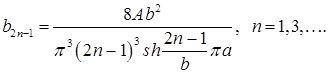 
Значит,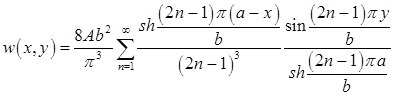 
.
Остается сложить найденные функции 
и 
.:
. ●
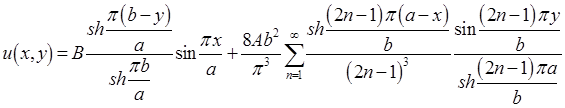Задача 2. Внутренняя задача Дирихле для кругового сектора:
найти гармоническую функцию внутри сектора
,
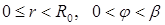удовлетворяющую на границе условиям
.
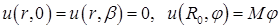Решение. Перейдем к полярным координатам 
и запишем оператор Лапласа в новой системе координат:
.
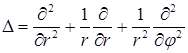Функция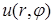 
есть решение задачи
, 
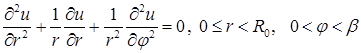
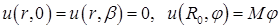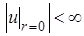
Нетривиальное решение уравнения Лапласа ищем в виде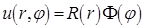 
.
После подстановки в уравнение и разделения переменных получаем
.
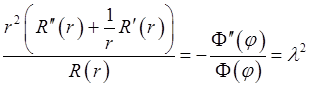Для уравнения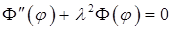 
запишем общее решение:
.
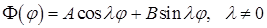Из условий на прямолинейных границах сектора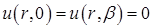 
следует, что 
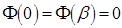. Тогда 
, 
, 
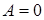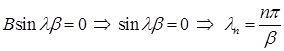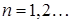–собственные значения и 
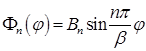– собственные функции.
Заметим, что при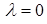 
получаем 
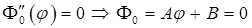в силу условий .
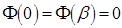Для функции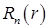 
получаем уравнение Эйлера
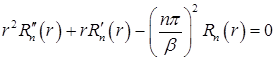
Разыскиваем решение этого уравнения в виде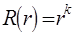 
. Тогда 
, 
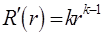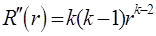и в результате приходим к характеристическому уравнению
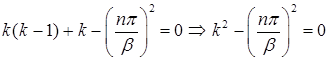
Корни этого уравнения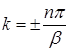 
. Значит, при 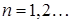линейно независимые частные решения суть 
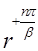и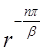 
, а общее решение записывается в виде
.
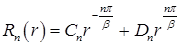В силу ограниченности решения при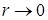 
следует положить 
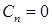. Поэтому функции 
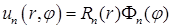имеют вид
.
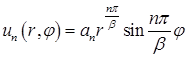Здесь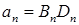 
.
Дальше действуем по стандартной схеме. Составляем ряд
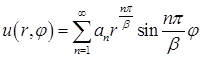
Коэффициенты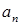 
подбираем так, чтобы удовлетворить условию 
:
.
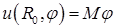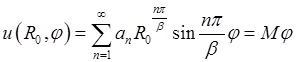Осталось разложить функцию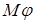 
в ряд Фурье по синусам на 
:
.
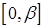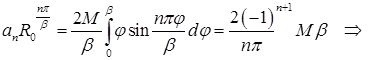
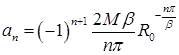Ответ: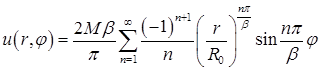 
. ●
Задача 3. Найти функцию, удовлетворяющую уравнению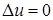 
в круге 
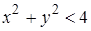при условии 
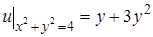(внутренняя задача Дирихле).
Решение. Перейдем к полярным координатам 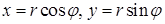в уравнении и краевых условиях:
.
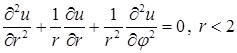
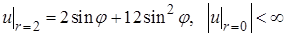Ищем решение в виде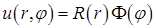 
. После подстановки в уравнение и разделения переменных получаем для функции 
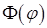уравнение
. 
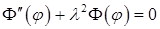
общее решение которого
.
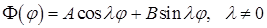Заметим, что в отличие от предыдущей задачи область здесь не сектор, где угол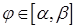 
. Поэтому роль граничных условий по аргументу 
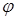играет периодичность функции 
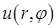. Действительно, увеличение аргумент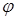а на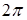 
возвращает точку 
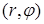в исходное положение; значит, все функции от 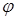, которые мы рассматриваем, должны быть периодическим по 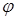с периодом 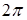. Таким образом, должно быть 
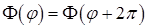. Это возможно только при 
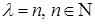. Отрицательные 
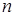можем не рассматривать, так как знак 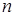влияет только на знак постоянной 
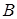. Итак, 
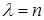– собственные числа и 
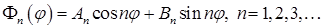.– собственные функции.
При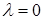 
получим уравнение 
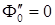, решением которого является линейная функция 
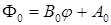. Условие 
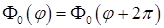выполняется, если 
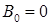. Значит, собственному значению 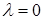соответствует собственная функция 
.
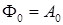Для определения функций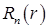 
получаем уравнение Эйлера
.
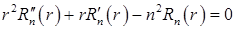Разыскивая решение этого уравнения в виде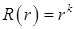 
, приходим к характеристическому уравнению 
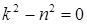, корни которого 
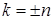. Значит, при 
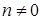линейно независимые частные решения суть 
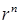и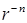 
. Второе из этих решений мы должны отбросить, так как при 
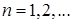оно обращается в бесконечность в центре круга 
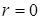. При 
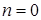получаем кратные корни 
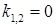, соответствующие линейно независимые решения суть 
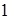и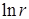 
. Логарифм отбрасываем из-за его неограниченности в нуле. Значит, общее решение уравнения Эйлера можно записать в виде
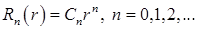
Замечание. Если бы требовалось решить внешнюю задачу Дирихле (найти функцию, гармоническую вне круга, по известному ее значению на границе), то требование ограниченности решения на бесконечности привело бы к отбрасыванию частных решени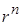й 
и .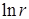
Получили функцию 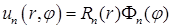в виде
, 
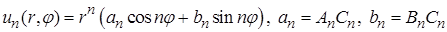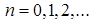
Составляем ряд
. (*)
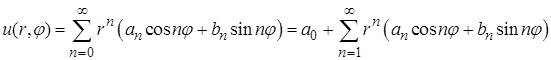Коэффициенты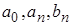 
определим из условия на границе круга 
:
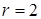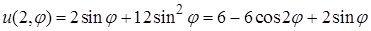
Полагаем :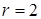
.
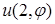
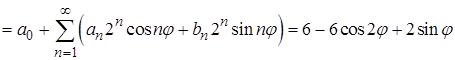Слева – разложение функции 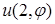в полный ряд Фурье на 
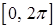, справа – несколько слагаемых из такого ряда.
Сравниваем коэффициенты Фурье:
свободный член: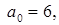 
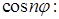
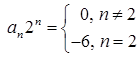
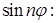
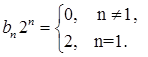
Отличны от нуля только коэффициенты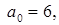 
.
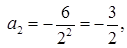
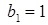Значит, из всего ряда (*) остаётся три слагаемых:
.
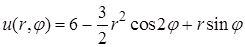Можно вернуться к переменным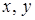 
:
●
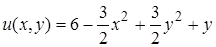Задача 4. Найти гармоническую в кольце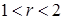 
функцию, удовлетворяющую на границе условиям 
.
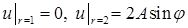Решение. Ищем решение уравнения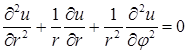 
в области 
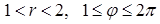в виде 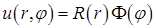. Как показано в задаче 3, для функции 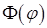получаем
.
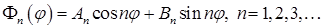
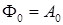Для определения функций 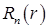получаем уравнение Эйлера
.
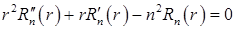При 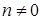линейно независимые частные решения суть 
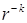и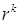 
, а общее решение уравнения имеет вид
.
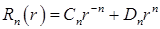При 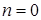линейно независимые решения суть 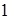и 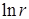, а общее решение
.
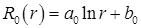Заметим, что все эти решения ограничены в заданной области.
Составляем ряд
. (**)
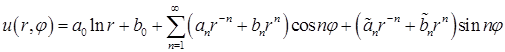Подберем коэффициенты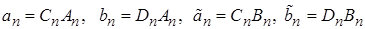 
так, чтобы удовлетворить граничным условиям.
Полагаем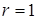 
:
. 
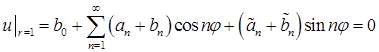Сравнивая коэффициенты, получаем соотношения:
Свободный член: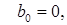 
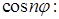
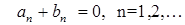
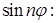
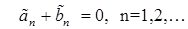
При 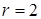получаем
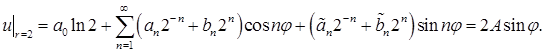
Ряд Фурье правой части содержит единственное слагаемое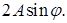 
Сравнивая коэффициенты, получим еще несколько соотношений:
Свободный член: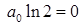 
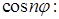
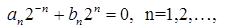
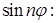
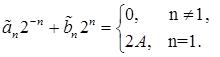
Для коэффициентов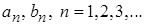 
имеем однородную систему с отличным от нуля определителем:
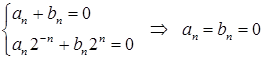
Коэффициенты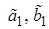 
находим из системы:
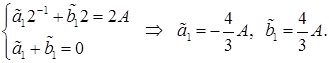
Наконец, для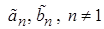 
получаем
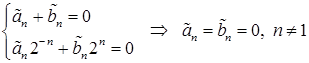
Из бесконечного ряда (**) остается только слагаемое, соответствующее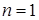 
:
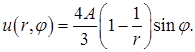
Можно преобразовать разность: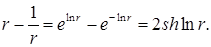 
Ответ: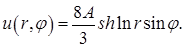 
●
Задача 5. Найти функцию 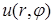, которая удовлетворяет внутри кольца 
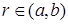неоднородному уравнению
,
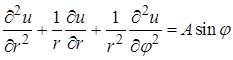а на границе принимает значения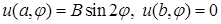 
.
Решение. Ищем решение в виде
,
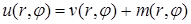где слагаемое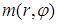 
должно удовлетворять граничным условиям. Полагаем
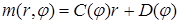
Коэффициенты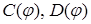 
определяем из системы
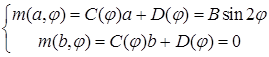
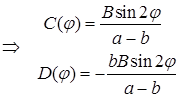
Значит,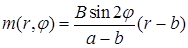 
.
Функция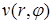 
удовлетворяет однородным граничным условиям и неоднородному уравнению 
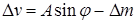, то есть
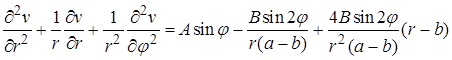
Представим правую часть в виде суммы
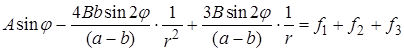
Линейность уравнения позволяет и решение искать в виде суммы
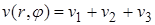
в соответствии со слагаемыми в правой части уравнения. При этом можем считать, что каждая из функций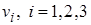 
равна нулю на границе, т.е. при 
.
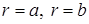1. Для правой части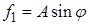 
ищем решение в виде 
.
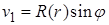Так как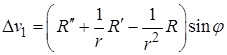 
, то функция 
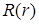есть решение уравнения Эйлера
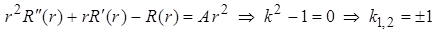
Общее решение однородного уравнения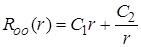 
. Частное решение 
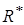находим по виду правой части: 
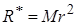. Тогда
.
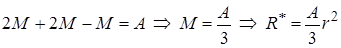Общее решение неоднородного уравнения:
.
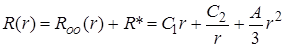Значит,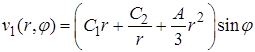 
Условия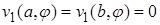 
приводят к системе для определения 
:
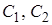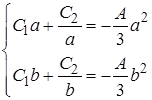
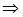
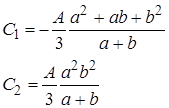
Получили функцию
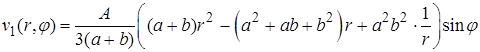
2. Для правой части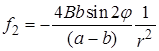 
решение 
.
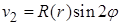Так как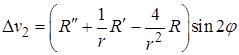 
, то приходим к уравнению
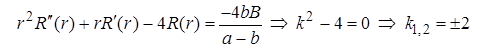
Общее решение однородного уравнения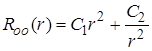 
, частное решение 
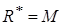. Очевидно, 
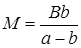, тогда 
.
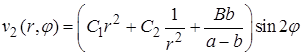Далее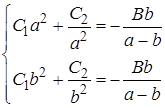 
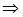
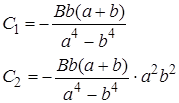
Получили функцию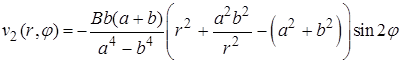 
.
3. Для правой части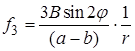 
ищем решение в виде 
.
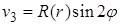Решая уравнение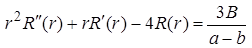 
, находим частное решение 
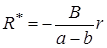, получаем , а затем и функцию
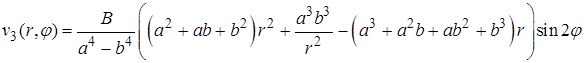
Остается сложить функции 
. ●