Пример 1. Доказать, что 
Доказательство. Возьмем произвольное сколь угодно малое 
и определим номер 
такой, чтобы выполнялось неравенство 
За 
возьмем целую часть 
. Итак, для произвольного найдется номер , что для всех 
будет выполняться неравенство 
, следовательно, число 4 является пределом последовательности.
Пример 2. Доказать, что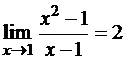 
.
Доказательство. Воспользуемся тем, что при рассмотрении предела функции в точке x=1 ее аргумент не принимает значения, равное 1. Имеем
при 
Возьмем любое . Тогда:
, если 
и Отсюда видно, что если взять 
, то для всех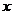 
, удовлетворяющих неравенству 
при , выполняется требуемое неравенство:
Это означает, что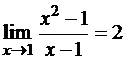
3 Неопределенность 
Неопределенности такого вида возникают при вычислении пределов типа: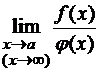 
, если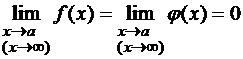 
При этом возможны частные случаи:
1) Числитель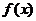 
и знаменатель 
дроби - многочлены.
Для вычисления предела необходимо разложить числитель и знаменатель на множители и сократить дробь на множитель, порождающий нуль.
Пример 3. Найти 
Решение. Разложим на множители числитель и знаменатель дроби:
2) Числитель или знаменатель дроби, или оба содержат иррациональность. Для решения примера необходимо освободиться от иррациональности, умножив числитель и знаменатель дроби на сопряженное выражение, сократить дробь на множитель, порождающий нуль.
Пример 4. Найти 
Решение. При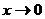 
числитель и знаменатель стремятся к нулю. Для раскрытия неопределенности 
умножим числитель и знаменатель на выражение, сопряженное знаменателю по формуле разности кубов. Тогда
получим: 
= 
3) Выражение содержит тригонометрические функции. Для решения примера необходимо путем тригонометрических и алгебраических преобразований свести его к первому замечательному пределу.
Пример 5. Найти 
Решение. Подстановкой предельного значения 
убедимся, что имеем неопределенность 
. Применяем тригонометрическую формулу 
, преобразуем полученное выражение, сводим к первому замечательному пределу. 
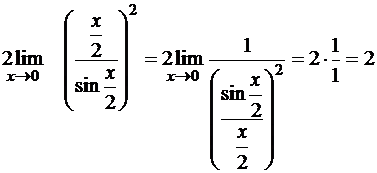
Пример 6. Найти 
Решение. Сделаем замену 
, т.е. 
Ясно, что 
при 
поэтому 
4 Неопределенность вида 
1) Числитель и знаменатель дроби при 
- полиномы.
Для раскрытия неопределенности целесообразно числитель и знаменатель разделить на степень с наивысшим показателем, а затем перейти к пределу.
Пример 7. Найти 
Решение. 
2) Пример 8. Найти 
Решение. Поделим числитель и знаменатель дроби на старшую степень n (выбираем из двух вариантов 
и 
), т.е на 
Тогда 
5 Неопределенность вида 
Для раскрытия этой неопределенности необходимо путем преобразования исходного выражения получить неопределенность вида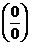 
или 
, т.е свести к предыдущим случаям 3,4
Пример 9. Найти 
Решение. 
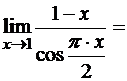
6 Неопределенность вида 
Этот случай нахождения предела функции можно привести к случаю 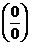или
путем преобразования функции к виду дроби.
Пример 10. Найти 
Решение. Рассматривая данную функцию как дробную со знаменателем, равным единице, избавимся от иррациональности в числителе и затем разделим числитель и знаменатель на x:
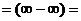
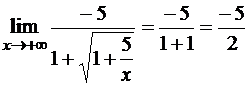
7 Неопределенность вида 
Неопределенности такого вида появляются при решении примеров вида:
, где 
, 
или 
, где 
, .
Преобразуя выражения, сводим их ко второму замечательному пределу.
Пример 11. Найти 
Решение. Полагая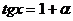 
, получим 
когда 
, и
,
, так как 
Комбинированные случаи
Для этих наиболее сложных случаев раскрытия неопределенностей общих рекомендаций нет. В каждом примере свой подход к решению. При достаточно хороших навыках в решении пяти предыдущих случаях, можно воспользоваться, приведенными выше рекомендациями.
Пример 12. 
Решение.
Имеем неопределенность вида 
. Это отчетливо видно, если с помощью свойств логарифма представить предел в виде:
= 
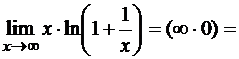
На основании непрерывности логарифмической функции перейдем к пределу под символом логарифма, т.е
