При решении задачи необходимо воспользоваться рекомендациями к заданию №2. Различие состоит в том, что балка закреплена при помощи шарнирно-неподвижной и шарнирно-подвижной опор, реакции которых и необходимо определить.
Пример решения задачи №3
Рисунок 3.1 – Схема балки
| Определить опорные реакции балки (рисунок 3.1) при следующих данных: Р=12 кН, М=16 кНм, q=3кН/м.
________________________
   
|
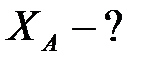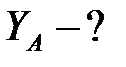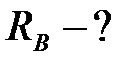
Решение:
1. Объект равновесия – балка АВ;
2. Заменяем связи реакциями: в подвижном шарнире -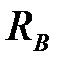 
, в неподвижном шарнире - 
, 
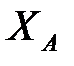. Распределенную нагрузку заменяем равнодействующей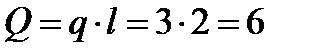 
кН (рисунок3.2).
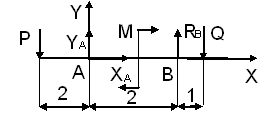
Рисунок 3.2. Расчетная схема балки
3. Выбираем направление осей координат X и Y;
4. Составляем и решаем уравнения равновесия:
4.1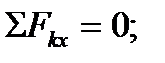 
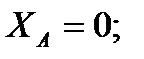
4.2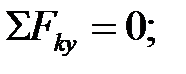 
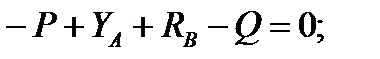
4.3 
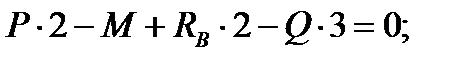
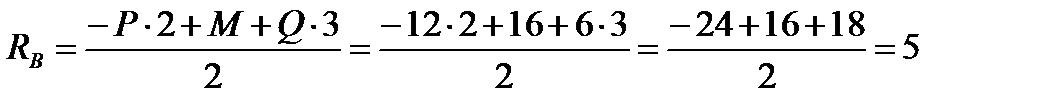(кН);
Из (4.2)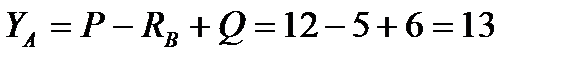 
(кН);
5. Проверяем найденные реакции связей. Для этого составляем выражение суммы моментов всех сил, приложенных к балке, относительно точки В:
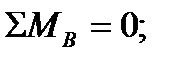
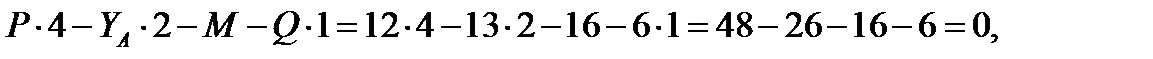следовательно, реакции опор вычислены правильно.
Вопросы для самопроверки
Для закрепления данной темы использовать вопросы к задаче № 2.
Задача №4
«Растяжение и сжатие. Определение внутренних усилий, напряжений и перемещений в поперечных сечениях бруса»
Задание: Ступенчатый стержень находится под действием осевых сил. Построить эпюры продольных сил, нормальных напряжений и перемещений. Стержень изготовлен из стали (модуль упругости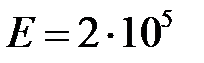 
МПа).
Варианты заданий к задаче №4
Таблица 4.1 – Схемы стержневых конструкций
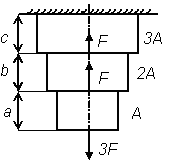Рис. 1
| 
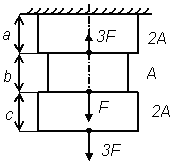Рис. 2
|
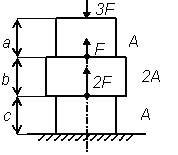Рис.3
| 
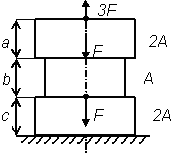Рис. 4
|
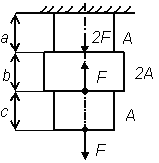Рис. 5
| 
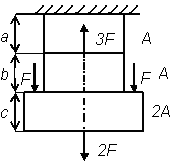Рис. 6
|
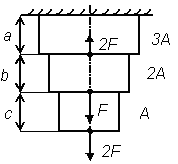Рис. 7
| 
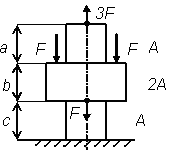Рис. 8
|
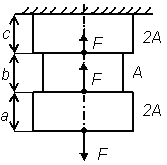Рис. 9
| 
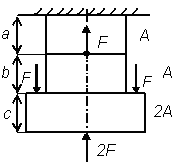Рис. 10
|
Таблица 4.2 – Численные данные к задаче № 4
| № варианта | № рисунка | F, кН | A, см2 | а, м | b, м | с, м |
| Рис. 1 | 1,2 | 0,8 | ||||
| Рис. 2 | 0,6 | 1,4 | ||||
| Рис. 3 | 0,8 | 0,8 | 1,4 | |||
| Рис. 4 | 1,2 | 1,4 | 1,4 | |||
| Рис. 5 | 1,5 | 1,5 | ||||
| Рис. 6 | 1,2 | 0,8 | ||||
| Рис. 7 | 0,6 | 1,4 | ||||
| Рис. 8 | 0,8 | 0,8 | 1,4 | |||
| Рис. 9 | 1,2 | 1,4 | 1,4 | |||
| Рис. 10 | 1,5 | 1,5 | ||||
| Рис. 1 | 1,2 | 0,8 | ||||
| Рис. 2 | 0,6 | 1,4 | ||||
| Рис. 3 | 0,8 | 0,8 | 1,4 | |||
| Рис. 4 | 1,2 | 1,4 | 1,4 | |||
| Рис. 5 | 1,5 | 1,5 | ||||
| Рис. 6 | 1,2 | 0,8 | ||||
| Рис. 7 | 0,6 | 1,4 | ||||
| Рис. 8 | 0,8 | 0,8 | 1,4 | |||
| Рис. 9 | 1,2 | 1,4 | 1,4 | |||
| Рис. 10 | 1,5 | 1,5 | ||||
| Рис. 1 | 1,2 | 0,8 | ||||
| Рис. 2 | 0,6 | 1,4 | ||||
| Рис. 3 | 0,8 | 0,8 | 1,4 | |||
| Рис. 4 | 1,2 | 1,4 | 1,4 | |||
| Рис. 5 | 1,5 | 1,5 | ||||
| Рис. 6 | 1,2 | 0,8 | ||||
| Рис. 7 | 0,6 | 1,4 | ||||
| Рис. 8 | 0,8 | 0,8 | 1,4 | |||
| Рис. 9 | 1,2 | 1,4 | 1,4 | |||
| Рис. 10 | 1,5 | 1,5 |
Краткие указания и пример решения задачи
Перед тем, как приступить к решению задачи, следует изучить тему «Растяжение и сжатие». Необходимо четко усвоить правила построения эпюр продольных сил и нормальных напряжений, закон распределения нормальных напряжений в поперечном сечении бруса, закон Гука, зависимости и формулы для расчета напряжений и осевых перемещений.
Примеррешения задачи №4
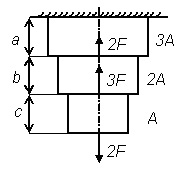Рисунок 4.1 – Стержневая конструкция
| Дано:
А = 10см2;
а = 2м; b = 2м; с = 2м;
F = 50 кН
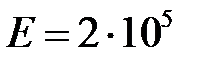 МПа
_______________________________
Определить:
N -? σ -? λ -?
|
Решение:
1. Построение эпюры внутренних усилий N.
Для этого разбиваем брус на участки, начиная от свободного края. Границами участков являются места приложения внешних сил.
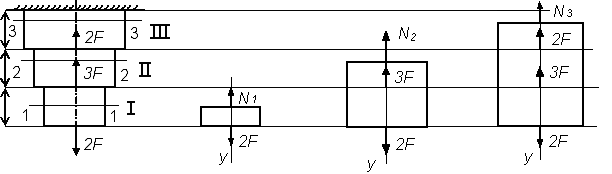Рисунок 4.2 – Применение метода сечений
|
Используем метод сечений. Проведя произвольное сечение 1-1 на участке I, отбросим верхнюю часть бруса и рассмотрим равновесие нижней части (рисунок 4.2), на которую действуют внешняя сила 2F и искомая продольная сила N1.
Составляем уравнение равновесия:
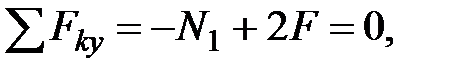откуда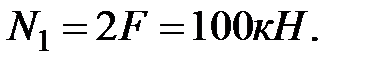 
Продольная сила N1 на участкеI постоянна и является растягивающей (направлена от рассматриваемого сечения).
Проводим сечение 2-2 на участке II и рассматриваем равновесие нижней отсеченной части (рис. 1.2.), на которую действуют внешние силы 2F и 3F и искомая продольная сила N2. Составляем уравнение равновесия:
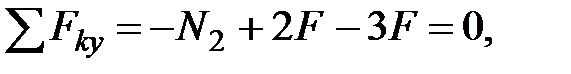откуда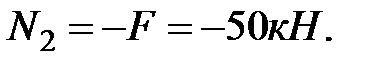 
В сечениях участка II продольная сила постоянна и является сжимающей.
Проведя сечение 3-3 на участке III, рассмотрим равновесие нижней отсеченной части (рис. 1.2.). Составляем уравнение равновесия:
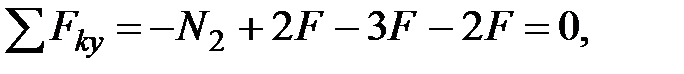откуда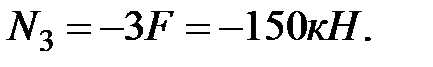 
В сечениях участка III продольная сила также сжимающая.
По полученным величинам продольных сил строим их эпюру (рис. 1.3.).
2. Построение эпюры нормальных напряжений σ.
Нормальные напряжения определяем по формуле:
,
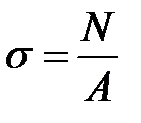где N – внутреннее усилие, Н;
А – площадь поперечного сечения, м2.
На участке I: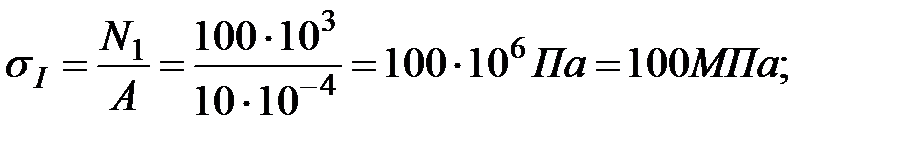 
На участке II: 
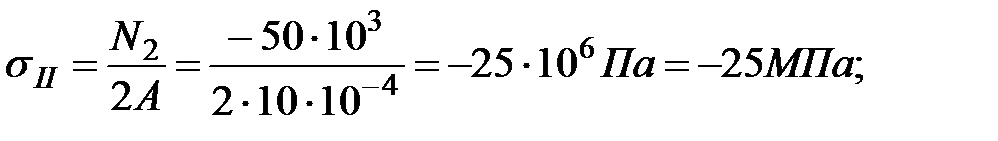
На участке III: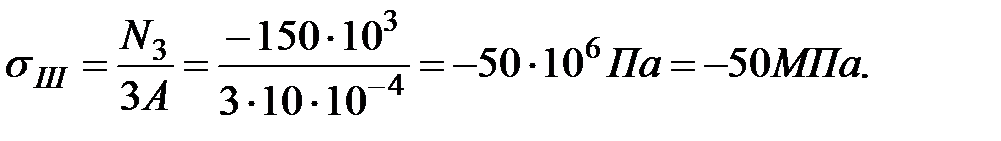 
По полученным данным строим эпюру нормальных напряжений (рисунок 4.3).
3. Построение эпюры перемещений λ.
Для построения эпюры достаточно определить перемещения сечений, совпадающих с границами участков, так как между ними эпюра линейна.
Сечение В-В неподвижно λв-в= 0.
Построение эпюры перемещений начинают всегда от неподвижного или условно принятого за неподвижное сечения.
Перемещение сечения С-С равно изменению длины (удлинению или сжатию) участка III стержня:
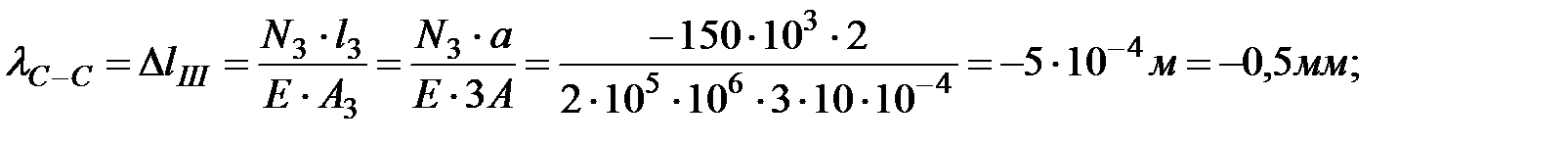Перемещение сечения D-D равно алгебраической сумме перемещения сечения C-C и изменению длины (удлинению или сжатию) участка II стержня:
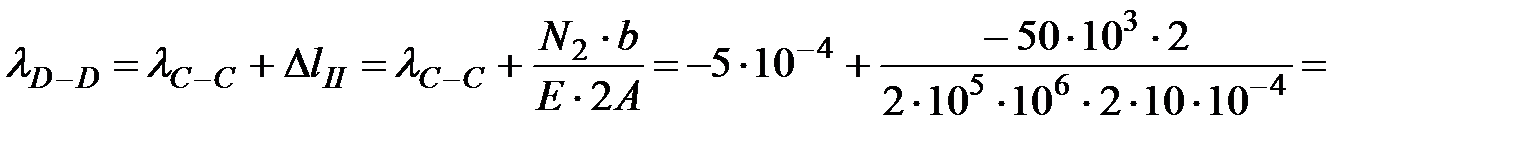
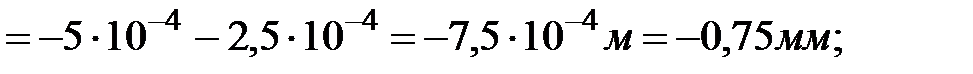
Перемещениесечения К-К равно алгебраической сумме перемещения сечения D-D и изменению длины (удлинению или сжатию) участка I стержня:
.
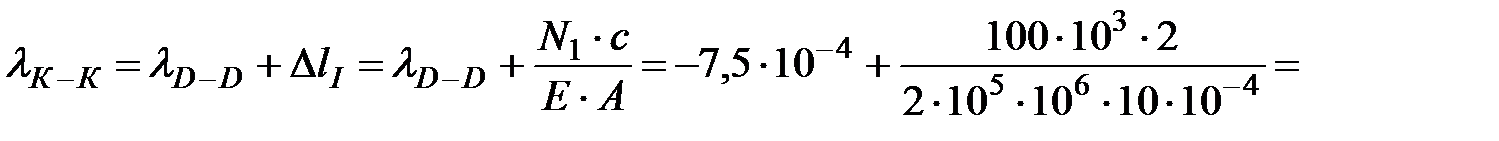
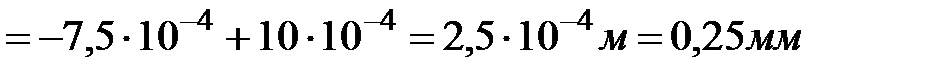По найденным значениям строим эпюру перемещений поперечных сечений стержня (рисунок 4.3).
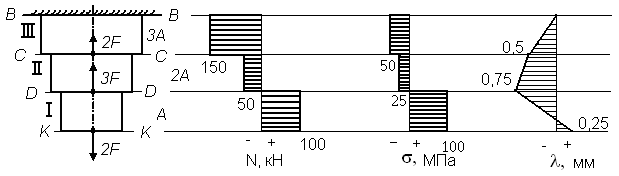Рисунок 4.3 – Эпюрыпродольных сил, напряжений и перемещений стержня
|
Вопросы для самопроверки
1. В чем заключаются деформации растяжения и сжатия?
2. В чем сущность метода сечений?
3. Что называется продольной силой в сечении стержня?
4. Что называется эпюрами продольных сил и нормальных напряжений? Как они строятся?
5. Как записывается и как формулируется закон Гука при растяжении (сжатии)?
6. Формула Гука, ее применение.
Задача №5
«Растяжение и сжатие. Подбор сечений стержней