Лабораторная работа 1. Расчет параметров парной линейной регрессии
Задание №1 для ВСК 1 (макс. балл 35) - сдача на 5 неделе.
Выполнить соответствующий вариант согласно расчетам, приведенным в типовой задаче. (номер варианта и исходные данные в файле "Инд. задания для лаб.1-2" Все расчеты выполняются в EXCEL)
Пример 1. Ферма занимается выращиванием пушного зверька. На основе содержательного анализа установили, что на ферме все технологические нормативы по содержанию и кормлению соблюдаются. Тогда масса зверька в основном зависит от его возраста.
Определим количественную зависимость массы пушного зверька У (кг) от его возраста Х (в месяцах) (таблица 3).
Таблица 3 - Исходные данные
| Хi-возраст, месяц | |||||||||
| Yi-масса, кг | 1.3 | 2.5 | 3.9 | 5.2 | 6.3 | 7.5 | 10.8 | 12,8 |
Задание:
1 Установить тесноту связи
2 Построить уравнение парной регрессии у от х.
3 Определите параметрыуравнения регрессии.
4 Проверить адекватность уравнения регрессии
5 Оценить статистическую значимость параметров регрессии
6 Определить доверительный интервал параметров регрессии
7 Выполнить прогноз у при прогнозном значении х.
8 Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
Решение. Для удобства решения задачи все расчеты выполним в табличном процессоре EXCEL и представим в следующей форме.
9 Для установления тесноты связи находим значение коэффициента корреляции r, для этого используем итоговые значении граф 8, 9 и 10.
Тогда
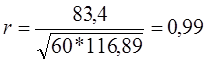
связь очень тесная, положительная. Коэффициент корреляции близок к 1. Определим коэффициент детерминации (r) 2= (0.99) 2=0,98. Вариация результата у на 98% объясняется вариацией фактора х, а 2% приходятся на неучтенные факторы. Если между выбранными факторами имеется тесная связь, то можно построить уравнение регрессии.
парная линейная регрессия интервал
Таблица 4 - Расчеты парной регрессии
| № | Хi | Yi | Xi-Xcp | Yi-Ycp | (Xi-Xcp) (Yi-Ycp) | (Xi-Xcp) 2 | (Yi-Ycp) 2 | Xi2 | Xi*Yi | Y* | Ai | (Y-Y*) 2 |
| 1,3 | -4 | -5,289 | 21,15555556 | 27,97235 | 1,0289 | 0, 2085 | 0,0735 | |||||
| 2,5 | -3 | -4,089 | 12,26666667 | 16,71901 | 2,5 | 2,4189 | 0,0324 | 0,0066 | ||||
| 3,9 | -2 | -2,689 | 5,377777778 | 7,230123 | 7,8 | 3,8089 | 0,0234 | 0,0083 | ||||
| 5,2 | -1 | -1,389 | 1,388888889 | 1,929012 | 15,6 | 5, 1989 | 0,0002 | 1E-06 | ||||
| 6,3 | -0,289 | 0,083457 | 25,2 | 6,5889 | 0,0459 | 0,0835 | ||||||
| 7,5 | 0,9111 | 0,911111111 | 0,830123 | 37,5 | 7,9789 | 0,0639 | 0,2293 | |||||
| 2,4111 | 4,822222222 | 5,813457 | 9,3689 | 0,041 | 0,1361 | |||||||
| 10,8 | 4,2111 | 12,63333333 | 17,73346 | 75,6 | 10,759 | 0,0038 | 0,0017 | |||||
| 12,8 | 6,2111 | 24,84444444 | 38,5779 | 102,4 | 12,149 | 0,0509 | 0,4239 | |||||
| ∑ | 59,3 | 83,4 | 116,8889 | 320,6 | 59,3 | 0,4699 | 0,9629 | |||||
| cредн | 6,5889 | |||||||||||
| Параметр | а= | 1,0289 | в= | 1,39 | Аср= | 5,2215 | R= | 0.9959 | R2= | 0.9818 |
| R2= | 0,9917624 | F= | 842,7577 | tr=29,03029 |
10 Для определение вида функции построим график зависимости у от х (рис. 3). Из рисунка видно, что точки располагаются вдоль прямой линии. Значит, выбираем линейную функцию, уравнение регрессии имеет вид у=а+в*х.
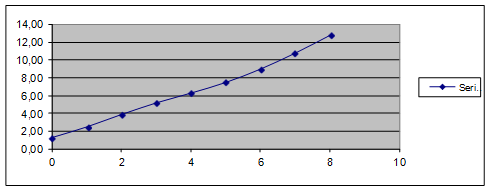
Рисунок 3 - График парной регрессии
2 Для определения параметров а и в используем формулу (6).
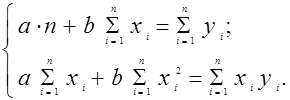 (6)
(6)
Используя итоговые расчеты 2-5 граф таблицы, получим систему уравнений
а+36в=59,3
а+204в=320,6
отсюда а=1,028, в=1,39, тогда уравнение регрессии у=1,028+1,39х. С увеличением возраста зверка на 1 кг, масса увеличивается в среднем на 1,39 кг.
Лабораторная работа 2. Продолжение лабораторной работы №1, т. е исходные данные из примера 1
Задание 2 для ВСК1 (макс. балл 35) - сдача на 13 неделе.)
Выполнить соответствующий вариант согласно расчетам, приведенным в типовой задаче. (номер варианта и исходные данные в файле "Инд. задания для лаб1-2" Все расчеты выполняются в EXCEL)
. Адекватность уравнения регрессии проверяется через вычисления значений Аср, tr и F. Найдем величину средней аппроксимации, для этого используем графу 13
Аср = (åАi) / n = 46,99/9 =5,22
Полученное значение Аср остается на допустимом уровне, так как не превышает 8-10%. Оценку статистической значимости модели регрессии проведем с помощью критерия Фишера Fфак и t - статистик Стьюдента.
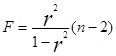 = 0.98/ (1-0.98) *7 = 0.98/0.02 *7=
= 0.98/ (1-0.98) *7 = 0.98/0.02 *7=
= 842,7577 Fтабл=5,12<Fфакт=343,
гипотеза о случайности факторов отклоняется. Критерий t-Стьюдента вычисляем по формуле 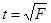 =29,03, значит tтабл= 2,26 < tфакт=18,5. Фактическое значение tr-критерия Стьюдента коэффициента корреляции определяется как
=29,03, значит tтабл= 2,26 < tфакт=18,5. Фактическое значение tr-критерия Стьюдента коэффициента корреляции определяется как 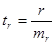 =
= 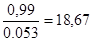 , здесь
, здесь
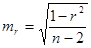 =
= 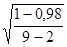 =0,053
=0,053
Соотношение tтабл=2,26<tфакт=18,67 означает, что тесная связь между у и х неслучайная. Масса зверка неслучайна зависит от возраста, если все другие факторы остается постоянным, то есть также будет соблюдаться все технологические нормативы.
Отсюда уравнение регрессии является адекватным, т. е полученное уравнение достоверно описывает количественную зависимость факторов у и х.
5. Оценку статистической значимости параметров регрессии проведем по формулам:
tb=b/mb. tа=a/ma.
Случайные ошибки параметров линейной регрессии определяются по формулам:
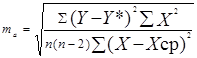 , ta =
, ta = 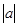 /ma,
/ma,
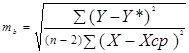 , tb =
, tb = 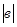 /mb.
/mb.
Для вычисления m2a используем 4, 9 и 14 графы таблицы 3
m2a= (0,96*204) / (9*7*60) =195,84/3780= 0.052, отсюда ma= 0,227
m2b= 0,96/ (7* 60) = 0,96/420=0,0023, отсюда mb =0.04788
Теперь находим ta= 1,028/0.227=4,53, tb=1.39/0.048= 29,03, Полученные статистические оценки параметров уравнения регрессии позволяют утверждать что, они статистически значимы и отражают устойчивую зависимость массы зверка от его возраста.
6. Доверительный интервал параметров регрессии вычисляется по формулам
а ±tкр*mа и b ±tкр*mb
Для этого определяем предельную ошибку D для каждого параметра
Dа =tтабл ma= 2.26*0.227=0.513, Db =tтабл mb=2.26*0.048=0.108.
Формулы для расчета доверительных интервалов имеют следующий вид:
gа = а± Dа =1,028± 0,513, gаmin = a - Dа =1,028 - 0.513=0.515
gаmax =a+ Dа =1,028+0.513=1.541,
Тогда параметр а будет в интервале 0.515<a<1.541.
Параметр в вычисляем также
gв = в± Dв =1,39 ±,18,gвmin = в -
Dв =1,39-0,108=1,282, gвmax =в+ Dв =1,39+0,108=1,498.
Тогда параметр в будет в интервале 1,282<в<1.498.
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
. Выполнить прогноз У при прогнозном значении Х
После этого полученное уравнение регрессии можно использовать для прогноза. Прогнозное значение Упрог определяется путем подстановки в уравнение регрессии У=1,028+1,39*х соответствующего (прогнозное) значения Хпрог.
Сбор данных осуществлен по периодам времени, то прогнозное значение х будет следующий период. Например, Хпрог=10, то Упрог=1,028+1,39*10= 14,93, это означает, что через месяц масса зверка будет в среднем 14,93 кг. Через два месяца в среднем будет Упрог=1,028+1,39*11= 16,32 кг.
8. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
Средняя стандартная ошибка прогноза за 10 период вычисляется по формулам:
m2 (Yпрог) = {å (у-у*) 2/ (n-m-1) } {1+ 1/n + (xпрог-хср) 2/ å ( x-xср) 2}=
= (0,96/7) * (1+1/9+36/60) = 0,137*1,711=0,234, отсюда m (yпрог) = 0,484
и строим доверительный интервал прогноза
gу =упр± Dпр= упр± tтабл my,
gуmin= упр tтабл my =14.93-2.26*0.484=13.84
gуmax= упр tтабл my=14.93+2.26*0.484=16.02.
Таким образом Упрогн будет в интервале [13,84; 16,02].
Регрессионный анализ на компьютере с помощью ППП Excel выполняется очень легко и быстро. Рассмотрим работу пакета для проведения регрессионного анализа. Для этого выполним следующие шаги:
1 Формируем таблицу исходных данных в среде Excel;
2 В главном меню выберите последовательно пункты
Сервис/Анализ данных/Корреляция/ОК;
3 Заполните диалоговое окно ввода данных и параметров вывода.
Входной интервал; выделите все столбцы, содержащие значения Х и У; В1; С10;
Выходной интервал; выделите область пустой ячейки для вывода результатов, например Д2; ОК.
Еxcel представит таблицу коэффициентов парной корреляции между У и Х.
Таблица 5 - Результаты решения задачи с помощью инструмента Корреляция
| № | х | y | ||||
| 1,30 | х | y | ||||
| 2,50 | х | |||||
| 3,90 | y | 0,9959 | ||||
| 5, 20 | ||||||
| 6,30 | ||||||
| 7,50 | ||||||
| 9,00 | ||||||
| 10,80 | ||||||
| 12,80 |
Таблица 5. показывает коэффициент корреляции между у и х ryx=0,9959.
4 Для вычисления параметров уравнения регрессии используем инструмент анализа данных Регрессия.
Алгоритм действий следующий: Сервис/Анализ данных/Регрессия/ОК;
Входной интервал У; выделите столбец содержащие значения У (столбец С1: С10;
Входной интервал Х; выделите столбец содержащие значения Х (столбец В1: В10;
Выходной интервал: выделите область пустых ячеек для вывода результатов, например В12;
Остатки; установите флажок;
Excel представит решение в виде таблиц 5-7.
Таблица 6 называется регрессионной статистики. В таблице представлено:
Коэффициент корреляции R=0.9959;
Квадрат коэффициента корреляции R2=0.9918;
Стандартная ошибка - S= 0.3709;
Таблица 7-Регрессионная статистика
| SUMMARY OUTPUT | |||
| Regression Statistics | |||
| Multiple R | 0,9959 | ||
| R Square | 0,9918 | ||
| Adjusted R Square | 0,9906 | ||
| Standard Error | 0,3709 | ||
| Observations |
Таблица 7 - Дисперсионный анализ представляет:
df =1 - число степени свободы;
SS - сумма квадратов разностей:
Сумма квадратов регрессии с числом степеней свободы 1 SS1=115,926.
Сумма квадратов остатков с числом степей свободы п-2 - SS2 =0,963.
Cумма квадратов общая с числом степеней свободы п-1 - SS=116,889
MS - оценка дисперсий:
дисперсия регрессии - d2факт=SS 1/1=115,926;
дисперсия остаточная d2ост = SS 2/ (n-2) =0.138;
F - критерий Фишера: F= 842,758.
Таблица 7-Дисперсионный анализ
| ANOVA | ||||||
| df | SS | MS | F | Significance F | ||
| Regression | 115,926 | 115,926 | 842,758 | 0,000 | ||
| Residual | 0,963 | 0,138 | ||||
| Total | 116,889 |
Таблица 8 - Параметры уравнения регрессии
В ней представлено:
Графа 2 показывает значения коэффициентов а и в:
а=1,028, в=1,39.
Графа 3 - Стандартная ошибка; ma = 0,228 и mb=0,0479;
Графа 4 - t - статистика; ta =4,5135, tb=29,0303.
Графа 5-6-Доверительные интервалы. Интервальные оценки gаmin=0,4899, gаmax= 1.5679. gвmin= 1.2768, gвmax= 1.5032для параметров регрессии с доверительной вероятностью р=0,95.
Таблица 8
| Coefficients | Standard Error | t Stat | P-value | Lower 95% | Upper 95% | |
| Intercept | 1,0289 | 0,2280 | 4,5135 | 0,0028 | 0,4899 | 1,5679 |
| х | 1,3900 | 0,0479 | 29,0303 | 0,0000 | 1,2768 | 1,5032 |
По результатам запишем уравнение регрессии.
У=1,0289+1,39*х,
Доверительные интервалы параметров регрессии
<a<1.5679, 1,2768<b<1.5032.
При расчетах двумя способами имеются погрешности, они связаны с округлением десятичных знаков до двух. Использование специального пакета ЕХСЕL обеспечивает точность вычисление.