Дюдин М.С.
Методические указания по выполнению контрольных работ по дисциплине "Основы финансовых вычислений"
для студентов бакалавриата, обучающихся по направлениям 38.03.02 "Менеджмент", 38.03.01"Экономика", 080500.62 "Бизнес-ифнорматика "
Рекомендовано Ученым советом Краснодарского филиала
(протокол № 14 от 20 октября 2015 г.)
Одобрено кафедрой «Математика и информатика»
(протокол № 2 от 7 октября 2015г.)
Краснодар 2015
Оглавление
1. Общие методические указания по выполнению.. 2
контрольной работы.. 2
2. Теория процентов. 3
3. Финансовые потоки. 9
4. Доходность и риск финансовой операции. 11
5. Портфельный анализ, облигации. 15
Рекомендуемая литература. 16
Общие методические указания по выполнению
Контрольной работы
Целью выполнения контрольной работы является проверка знаний студентов по дисциплине «Основы финансовых вычислений». Контрольные выполняются в письменном виде по указанным ниже вариантам. Решение задач должно содержать записанное в краткой форме условие, формулы, по которым проводятся расчеты, вычисления и ответ. Допускается округление ответа до сотых. Переписывать условие задач полностью не требуется.
Общая сумму баллов за контрольную работу составляет 100 баллов, которые затем переводятся в значение, указанное в технологической карте по дисциплине. Правильно решенные задачи оцениваются одинаково, по 14,28 балла. Вариант выбирается по последней цифре в зачетной книжки. По работам, выполненным не по своему варианту засчитывается 0 баллов.
| Последняя цифра номера зачетной книжки: | Вариант | Номера задач: | |||||||||
| - | - | ||||||||||
| - | - | ||||||||||
| - | - | ||||||||||
| - | - | ||||||||||
| - | - | ||||||||||
| - | - | ||||||||||
| - | - | ||||||||||
| - | - | ||||||||||
| - | - | ||||||||||
| - | - |
Теория процентов
|
|
При предоставлении услуг по денежным займам кредитор получает вознаграждение, пропорциональное сумме займа 
и сроку займа n. Величина этого вознаграждения определяется процентом i. (процент i при вычислениях берется в виде десятичной дроби, например если ставка процента составляет 20%, то i =0,2)
Формула 
называется формулой наращения для простых процентов.
1. Предприятие берет в банке займ на сумму 500 т.р. сроком на 2 года под простую процентную ставку 10%. Определить, какую сумму нужно будет вернуть в банк в конце срока.
2. Определите, на какой срок следует взять кредит на сумму 250 т.р. что бы вернуть в банк не более 300т.р., если простая ставка составляет 15%.
3. Какую процентную ставку по кредиту на сумму 200 т.р. должен назначить банк, что бы через 2 года получить не менее 250 т.р.?
4. Через какое время удвоится сумма долга при простой ставке 6%?
5. Клиент вкладывает в банк сумму 100 т.р. сроком на 1 год под простую ставку 10%, затем забирает вклад вместе с процентами и вкладывает полученную сумму в другой банк сроком на 1 год под тот же процент. Какую сумму он получит? В случае, если бы вкладчик не снимал деньги со счета, а оставил бы их в первом банке на 2 года, какую сумму он бы получил?
|
|
Капитализацией процентов, или начислением процентов на проценты, называется причисление процентов к основной сумме вклада. Начисление процентов может происходить как раз в год, так и несколько раз в год. Рассмотрим случай, когда начисление процентов происходит раз в год:
Формула называется формулой наращения для сложных процентов.
6. В банке берется кредит 250 тысяч рублей сроком на 3 года под сложную процентную ставку 14%. Определить сумму, которую будет должен вернуть заемщик.
7. В банке берется кредит 150 тысяч рублей под сложную процентную ставку 14%. Определить время, через которое сумма долга превысит 200 т.р..
8. В банке берется кредит 180 тысяч рублей сроком на 1 год под сложную процентную ставку 14%. Определить наращенную стоимость кредита.
9. Определить, за какое время вклад в банк при ставке сложных процентов 15%
а) удвоится;
б) утроится.
10. Через какое время удвоится сумма долга при сложной ставке 5%?
В случае, если проценты начисляются m раз в год, применяется формула:
11. Определить величину реальной процентной ставки, если номинальная составляет 15%, а величина инфляции – 12%.
12. Какую ставку надо назначить по вкладу, что бы реальная ставка составила 5% при темпе инфляции 10%?
13. Какие проценты выгоднее для кредитора – сложные или простые?
a) Для срока более года.
б) Для срока менее года.
|
|
Когда срок займа n не является целым, возникает вопрос об оценке его дробной части. Выделают 3 подхода, британские проценты (точные проценты), которые подразумевают вычисление точного количества дней в месяце и в году (обозначается 365/365), германские проценты, когда для простоты вычислений берется приближенное количество дней в месяце, 30 дней, и приближенное количество дней в году, 360, (360/360) и французские проценты, когда количество дней в месяце берется приближенно, а в году - точно. (360/365)
Пример 1:
Кредит на сумму 100 тысяч рублей берется 5 января 2016 года сроком до 15 февраля 2017 года под сложную ставку 10%. Определить, какую сумму должен вернуть должник.
Срок займа составляет 1 год плюс дробный остаток в виде 25 дней в январе и 15 дней в феврале.
А) британские проценты
n=1+ 
=1,1123 (в числите вычитается 5 так как кредит взят 5 января)
; 
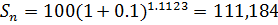т.р.
Б) германские проценты
В отличии от британских процентов, количество дней в январе приближенно берется равным 30, количество дней в году - 360
n=1+ 
=1,1096
; 
т.р.
В) французские проценты
Количество дней в январе берется равным 31, количество дней в году - приближенно, равным 360.
n=1+ 
=1,125
; 
Как видно из примера разница между разными видами процентов незначительная. Но при проведении финансовых операций с кредитами на большие сумм и длительные сроки даже небольшая разница в значении может изменить итог операции на существенную сумму.
14. 1 октября 2015-го года берется кредит на сумму 120 тысяч рублей сроком до 1 марта 2016-го года под сложную ставку 16%. Определить, какую сумму должен вернуть должник если используется
а) британская практика начисления процентов;
б) французская практика начисления процентов.
15. 20 ноября 2015-го года берется кредит на сумму 300 тысяч рублей сроком до 15 апреля 2016-го года под сложную ставку 14%. Определить, какую сумму должен вернуть должник если используется
а) британская практика начисления процентов;
б) немецкая практика начисления процентов.
16. 15 сентября 2015-го года берется кредит на сумму 270 тысяч рублей сроком до 20 мая 2016-го года под сложную ставку 15%. Определить, какую сумму должен вернуть должник если используется
а) британская практика начисления процентов;
б) немецкая практика начисления процентов.
17. 2 октября 2015-го года берется кредит на сумму 170 тысяч рублей сроком до 20 апреля 2016-го года. Определить, какую процентную ставку должен определить кредитор, что бы получить в конце срока от должника не менее 220 тысяч рублей. Использовать точные проценты.
18. 20 января 2016-го года берется кредит на сумму 215 тысяч рублей под сложную ставку 14%. Определить, какого числа должнику следует вернуть долг, что бы не заплатить более 250 тысяч рублей. Использовать германские проценты.
При переносе погашения финансового обязательства на более ранний срок возникает необходимость пересчета его стоимости в связи с уменьшением срока займа и соответственно процентов по займу. В этом случае применяется операция, обратная операции наращения, дисконтирование.
Существует два вида дисконтирования, банковский учет и математическое дисконтирование. При банковском учете для простых и сложных процентов используются формулы:
где d - учетная ставка, определяемая банком. Математическое дисконтирование обратно операции наращения и представляет из себя выражение 
из формул наращения для простых и сложных процентов:
Математическое дисконтирование используется при вычислениях стоимости финансовых потоков и рент.
19. Вексель стоимостью 270 т.р. погашается на 3 года и 2 месяца раньше срока. При какой сложной учетной ставке владелец получит 190 т.р.?
20. Вексель стоимостью 300 т.р. погашается на 2 года и 3 месяца раньше срока. При какой сложной учетной ставке владелец получит 215 т.р.?
21. Когда нужно погасить вексель стоимостью 400т.р. и с датой 1.12.14, что бы получить не менее 350 т.р. при сложной учетной ставке 30%?
22. Вексель стоимостью 500т.р. погашается на 3 месяца раньше срока, простая учетная ставка составляет 20%. Какую сумму получит владелец?
23. Вексель стоимостью 300т.р. погашается на полгода раньше срока, сложная учетная ставка составляет 25%. Какую сумму получит владелец? (использовать банковский учет)
24. Какая учетная ставка выгоднее банку, рассчитывающемуся с владельцем векселя, погашаемого раньше срока – сложная или простая?
Финансовые потоки
На практике часто встречаются случаи, когда финансовые обязательства погашаются не одномоментно, а растягиваясь по времени. Финансовым потоком называется поступление платежей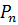 
в различные моменты времени n, и обозначается как CF={(
; 
),(
; 
),...,(
; 
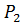)} (CF - cash flow) Для удобства расчетов финансовый поток можно изобразить на временном графике:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
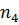
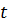
Стоимость финансового потока неравноценна в различные моменты времени из-за необходимости выплачивать проценты за пользование капиталом. Поэтому для оценки финансового потока применяются величины:
Современная стоимость, PV (present value) оценивается формуле:
то есть каждый платеж 
приводится к начальному моменту времени и затем суммируется с остальными.
Наращенная стоимость, FV (future value) оценивается формуле:
то есть каждый платеж приводится к времени последнего платежа в потоке 
и затем суммируется с остальными.
Приведенная к моменту времени t стоимость, 
оценивается формуле:
то есть каждый платеж приводится к моменту времени t затем суммируется с остальными.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
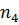
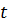
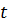
25. Рассчитать современную стоимость финансового потока CF={(0,-200),(1,150),(2,200),(3,150)}.
26. Рассчитать наращенную стоимость финансового потока CF={(0, 100),(1,150),(2,200),(3,200)}.
27. Рассчитать наращенную стоимость финансового потока CF={(0, 100),(2,250),(3,100),(4,100)}.
28. Рассчитать приведенную на момент времени t=2 стоимость финансового потока CF={(0, 200),(1,250),(2,300),(4,400)}.
29. Рассчитать приведенную на момент времени t=3 стоимость финансового потока CF={(0, 100),(2,150),(3,200),(4,250)}.
30. Сколько лет нужно вкладывать в банк по 10 тысяч в месяц, что бы накопить 350 тысяч рублей при банковской ставке 10%?
31. Какую сумму можно накопить, если 10 лет вкладывать в банк по 5 тысяч в месяц прибанковской ставке составляет 12%?
32. Что выгоднее, получить в данный момент 500 тысяч рублей или в течении 10 лет получать 5 тысяч в месяц, если процентная ставка составляет10%?
33. Определить современную стоимость аренды квартиры за 15000р. в месяц в течении двух лет, если ставка по банковскому вкладу составляет 10%.
34. Определить наращенную стоимость финансовой ренты с платежом 50000р., начислением процентов раз в полгода, сроком на 5 лет.
Доходность и риск финансовой операции
Доходность финансовой операции определяется по формуле
, где - сумма на начло операции, 
- сумма на конец операции.
Риск финансовой операции оценивается по стандартному отклонению ожидаемой доходности. Стандартное отклонение случайной величины равно корню из дисперсии.
Если стандартное отклонение известно не для доходностей, а для абсолютного значения величины 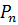, стандартное отклонение доходностей можно получить делением на .
35. Банк выдал кредит сроком на 2 года под сложные проценты 5%. Определить доходность этой финансовой операции.
36. Банк выдал кредит сроком на 3 года под простые проценты 7%. Определить доходность этой финансовой операции.
37. Определить риск покупки валюты с последующей конвертацией обратно в рубли, если курс покупки - 50 рублей, ожидаемый курс продажи - случайная величина со средним, равным 60 рублей и дисперсией, равной 9.
38. Определить риск покупки валюты с последующей конвертацией обратно в рубли, если курс покупки - 65 рублей, ожидаемый курс продажи - случайная величина со средним, равным 70 рублей и дисперсией, равной 16.
Теория игр рассматривает вопросы принятия решений в неопределенных ситуациях. Для выбора оптимального решения предлагается составлять матрицы, содержащие последствия различных решений в различных внешних обстоятельствах. Для выбора оптимального решения существует несколько критериев:
Критерий крайнего пессимизма, (критерий Вальда) когда для каждого из возможных решений выбирается самые негативные последствия, (в каждой строке выбирается минимальное значение) а из них выбирается наиболее предпочтительное. (из выбранных значений выбирается максимальное.
Критерий минимального риска, (критерий Сэвиджа) предусматривающий запись матрицы рисков, когда в каждом столбце выбирается максимальный элемент, и элементы столбца заменяются разницей максимального элемента и старого значения. (риск оценивается как убыток в сравнении с наилучшим решением)
Затем среди возможных решений выбирается самые негативные последствия, с максимальным риском (в каждой строке выбирается максимальное значение) а из них выбирается наиболее предпочтительное. (из выбранных значений выбирается значение с минимальным риском).
Критерий максимизации среднего ожидаемого дохода применяется, когда известны вероятности наступления возможных ситуаций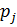 
. Выбирается решение, которое даст максимальный средний ожидаемый доход, оцениваемый, как сумма произведений дохода в ситуации j на вероятность наступления ситуации j.
Критерий минимизации среднего ожидаемого риска - аналогичен предыдущему критерию, но применяется для матрицы рисков.
Критерий Лапласса применяется, если значения вероятностей неизвестны. Тогда вероятности 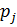берутся равными единице, деленной на количество столбцов.
39. Дана матрица последствий ||q||:
| Ситуация 1 | Ситуация 2 | Ситуация 3 | |
| Решение 1 | |||
| Решение 2 | |||
| Решение 3 |
Определить оптимальное решение по правилу Вальда (крайнего пессимизма)
40. Дана матрица последствий ||q||:
| Ситуация 1 | Ситуация 2 | |
| Решение 1 | ||
| Решение 2 | ||
| Решение 3 |
Определить оптимальное решение по правилу Сэвиджа (минимального риска)
41. Дана матрица последствий ||q||:
| Ситуация 1 | Ситуация 2 | Ситуация 3 | |
| Решение 1 | |||
| Решение 2 | |||
| Решение 3 |
Вероятность наступления ситуации 1 – 20%, ситуации 2 – 30%, ситуации 3 – 50%. Определить оптимальное решение по правилу максимизации среднего ожидаемого дохода.
42. Дана матрица последствий ||q||:
| Ситуация 1 | Ситуация 2 | Ситуация 3 | |
| Решение 1 | |||
| Решение 2 | |||
| Решение 3 |
Вероятности наступления ситуаций 1-3 неизвестны. Определить оптимальное решение по правилу Лапласа.
43. Дана матрица последствий ||q||:
| Ситуация 1 | Ситуация 2 | |
| Решение 1 | ||
| Решение 2 | ||
| Решение 3 |
Вероятность наступления ситуации 1 – 35%, ситуации 2 – 40%, ситуации 3 – 25%. Определить оптимальное решение по правилу минимизации среднего риска.