Принятие решений по критериям Лапласа, Вальда, Гурвица, Сэвиджа, Байеса теории статистических игр

В теории статистических игр условия выполнения операции зависят от

объективной действительности, которую в теории игр принято называть «природой». Соответствующие ситуации называют «играми с

природой» (статистическими играми). «Природа» в теории игр

рассматривается как некая незаинтересованная инстанция, поведение которой хотя и неизвестно, но, во всяком случае, не содержит элемента сознательного противодействия нашим планам. Пусть сторона А имеет возможных стратегий [6]

О состоянии «природы» можно сделать предположений

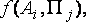Для каждой пары стратегий ( ) существует функция которая является случайной величиной и называется функцией потерь.

Пусть удаётся определить величину − эффективность решения в условиях для всех комбинаций пар стратегий . В этом случае платёжная матрица игры имеет вид:

В теории статистических игр, помимо платёжной матрицы, используется и, так называемая, матрица рисков или матрица сожалений.

Риском стороны А при использовании стратегии в условиях называется величина

(2.14)

где − максимальный выигрыш стороны А в состоянии «природы» П_J. 26

Критерий Лапласа основан на предположении, что каждый вариант развития ситуации (состояния «природы») равновероятен. Для каждой строки матрицы выигрышей подсчитывается среднее арифметическое значение оценок. Оптимальному решению будет соответствовать такое решение, которому соответствует максимальное значение среднего арифметического, т.е.

_n

F*= F(X*,Y)= max (1/n) ∑ a_ij (2.15)

^{j =1}

F*= F(X*,Y)= max min a_ij, (2.16)

_{1≤i≤m 1≤j≤m}

Этот критерий очень осторожен. Он ориентирован на наихудшие условия, только среди которых и отыскивается наилучший и теперь уже гарантированный результат. Критерий Вальда основывается на предположении, что произойдет наиболее худший вариант развития ситуации и риск наихудшего варианта нужно свести к минимуму.

Критерий Сэвиджа. Сущность этого критерия заключается в минимизации

риска. Как и критерий Вальда, критерий Сэвиджа очень осторожен. Они

различаются разным пониманием худшей ситуации: в первом случае — это минимальный выигрыш, во втором — максимальная потеря выигрыша по

сравнению с тем, чего можно было бы достичь в данных условиях. В каждом столбце матрицы находится максимальная оценка max а_ij и составляется новая матрица, элементы которой определяются соотношением (2.14) для r_ij . Под риском r_ij понимают разность между максимальным выигрышем, который имел бы место, если бы было достоверно известно, что наступит ситуация y_j,, и выигрышем при выборе решения х_i в условиях y_j.. Далее из матрицы рисков выбирают такое решение, при котором величина риска принимает наименьшее значение в самой неблагоприятной ситуации, т.е.

F*= F(X*,Y)= max min (max a_j -a_ij ) _, (2.17)

_{1≤i≤m 1≤j≤n 1≤i≤m}

Сущность этого критерия заключается в минимизации риска. Как и критерий Вальда, критерий Сэвиджа очень осторожен. Они различаются разным пониманием худшей ситуации: в первом случае — это минимальный выигрыш, во втором — максимальная потеря выигрыша по сравнению с тем, чего можно было бы достичь в данных условиях.

Критерий Гурвица -- критерий «оптимизма - пессимизма» ЛПР. Вводится коэффициент оптимизма, с которой произойдет наилучший для ЛПР исход, наихудший вариант можно ожидать с вероятностью (1-α), 0< α <1.

В каждой строке матрицы выигрышей находится самая большая оценка max а_ij и самая маленькая min a_ij.

Они умножаются соответственно на α и (1 — α) и затем вычисляется их сумма. Оптимальному решению будет соответствовать такое решение, которому соответствует максимум этой суммы, т.е.

28

F*= F(X*,Y)= max [ α max a_ij + (1- α )min a_ij ] _, (2.18)

_{1≤i≤m 1≤j≤n 1≤j≤n}

При α = 0 критерий Гурвица трансформируется в критерий Вальда. Это случай крайнего «пессимизма». При α = 1 (случай крайнего «оптимизма») человек, принимающий решение, рассчитывает на то, что ему будет сопутствовать самая благоприятная ситуации. «Коэффициент оптимизма» а назначается субъективно, исходя из опыта, интуиции и т.п. Чем более опасна ситуация, тем более осторожным должен быть подход к выбору решения и тем меньшее значение присваивается коэффициенту α

Критерий Байеса. За оптимальную стратегию принимается чистая стратегия при которой величина достигает наибольшего значения. С помощью этого критерия задача принятия решения в условиях неопределённости сводится к задаче принятия решения в условиях определённости, только принятое решение является оптимальным не в каждом отдельном случае, а в среднем. По критерию Байеса, оптимальной будет та стратегия при которой минимизируется величина среднего риска

(2.19)

Стратегия, максимизирующая средний выигрыш, совпадает со стратегией, минимизирующей средний риск.

Стратегия, максимизирующая средний выигрыш, совпадает со стратегией минимизации риска.

Пример выбора стратегии по критериям Лапласа, Вальда, Гурвица, Сэвиджа, Байеса. При планировании операции в заранее неясных условиях, относительно которых можно сделать различные предположения

Задана платёжная матрица

1. Критерий Вальда. В каждой строке платёжной матрицы выбираем наименьший выигрыш и из полученных значений берём наибольшее:

Следовательно оптимальной является стратегия

2. Критерий Сэвиджа. Построим сначала матрицу сожалений Для этого вычислим максимальные выигрыши стороны при трёх различных состояниях «природы»:

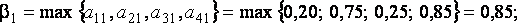
Теперь можем вычислить элементы матрицы сожалений:

Матрица сожалений имеет вид:

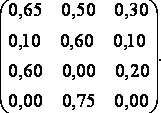
В каждой строке матрицы сожалений выберем наибольший риск и из полученных значений отметим наименьшее:

Следовательно, согласно критерию Сэвиджа, оптимальными являются стратегии и

3. Критерий Гурвица. В каждой строке платёжной матрицы определяем лри коэффициенте оптимизма α=0,6 наименьший и наибольший выигрыши и соответственно, а затем для каждой строки вычисляем величину :

По критерию Гурвица при α=0,6 оптимальной является стратегия