Задание на курсовой проект
Курсовая работа по дисциплине «Электромагнитная совместимость и средства защиты» - это комплексная самостоятельная работа обучающегося. Темой курсовой работы является «Расчет характеристик питания нагрузок в сети электроснабжения железных дорог».
Для заданной схемы (рис. 1) рассчитать коэффициенты n-ой гармонической составляющей напряжения, коэффициент несинусоидальности на шинах 110 и 6 кВ, дополнительные потери мощности и снижение срока службы трансформатора собственных нужд Т4 и асинхронного двигателя М из-за перегрева токами высших гармоник и несимметрии напряжения. Нормальный срок службы принять 20 лет.
Исходные данные:
Рабочая температура 750 С.
С: Sкз,110 = 1900 МВА; Sкз,6=170 МВА; Sкз,0,4=3 МВА
Т2: SТ2=50 МВА; Uном=110 кВ
Т3: SТ3=10 МВА; Uном=6 кВ; uк,%=10,5%
Т4: SТ4=1 МВА; Uном=6 кВ; uк,%=5,5%; ∆Ркз=10,5 кВт; ∆Рхх=1,9 кВт
М: РМ = 280 кВт; cos φ=0,9; Км=1,2; К1=5,1
VD: Sпр=8 МВА; cos φ=0,8; m=6
Н: Sнагр=2 МВА; Sab=4 МВА
Расчет коэффициента несинусоидальности на шинах 110 и 6 кВ.
Самой распространенной схемой выпрямления для мощных преобразователей является трехфазная мостовая схема (схема Ларионова), представленная на рис. 2. Эта схема выпрямления позволяет осуществить так называемую шестифазную или шестиимпульсную схему выпрямления. Соединение последовательно или параллельно двух или нескольких выпрямительных мостов при питании их напряжением, сдвинутым на соответствующий угол, позволяет получить 12, 18, 24, 36, 48...-фазные схемы выпрямления (кратные шести). Сдвиг угла напряжения осуществляется применением соответствующих схем соединения первичных или вторичных обмоток трансформатора: Υ — звезда, Δ— треугольник, Z — зигзаг, которые позволяют осуществить практически схемы любой фазности (импульсности) выпрямления.
Рис. 2 Схемы полупроводниковых преобразовательных агрегатов: а — агрегат до 6300 А шестифазного режима выпрямления (трехлинейная схема); б — однолинейная схема; в — трехлинейная схема агрегата 12500 А двенадцати- фазного режима выпрямления; г — однолинейная схема; д — однолинейная схема агрегата 25 000 А и его коммутационная аппаратура
Первичным является появление в питающей сети коммутационных искажений напряжения, а гармонический анализ их позволяет выявить наличие высших гармоник напряжения. Порядок высших гармоник определяется формулой n = тk ± 1, где т - число фаз выпрямления; k=0, 1, 2, 3... - последовательный ряд натуральных чисел.
Для шестифазной системы напряжения в кривой питающего напряжения имеются высшие гармоники следующего порядка, называемые каноническими: n=5, 7, 11, 13, 17, 19, 23...; для 12-фазной схемы n=11, 13, 23, 25, 35, 37...; для 24-фазной схемы n=23, 25, 47, 49, 71, 73 и т. д.
Методика расчета коэффициента несинусоидальности напряжения kU основывается на вычислении в любой точке питающей сети действующих значений коммутационных искажений напряжения, что равносильно учету всех высших гармоник. Следовательно, для определения kU при работе вентильных преобразователей нет необходимости определять уровни отдельных гармоник. При этом удается избежать ошибки, возникающей при учете только определенного числа высших гармоник.
Методика позволяет вычислять kU в любой точке питающей сети, используя параметры, полученные при вычислении токов КЗ, и основывается на следующих допущениях: проводимости элементов питающей сети считаются неемкостными. При этом допущении ошибка в расчете не превышает 10—15%. Предполагается, что в узлах сети, расположенных в непосредственной близости от вентильных преобразователей, отсутствуют конденсаторные батареи, предназначенные для компенсации реактивной мощности; не учитываются анормальные гармоники.
Коэффициент несинусоидальности напряжения питающей сети определяется по формуле [2]:
∙100 (1)
Общий коэффициент несинусоидальности питающей сети при работе вентильных преобразователей может быть определен по формуле [2]:
(2)
где 
- эквивалентное сопротивление системы в относительных единицах, приведенное к мощности преобразователя Snp, т. е. сопротивление от условной точки сети бесконечной мощности до точки сети, в которой определяется kU;
SKЗ — мощность КЗ в точке, в которой определяется kU;
хпр — индуктивное сопротивление цепи преобразователя в относительных единицах, приведенное к Snp, т. е. сопротивление от точки возникновения коммутационных КЗ до точки, в которой определяется kU.
Формула (3) справедлива для преобразователей с любой последовательностью чередования фаз.
Кроме коэффициента несинусоидальности ГОСТ нормирует коэффициенты n-ой гармонической составляющей. Согласно [4]:
(3)
При определении kU особое внимание следует обращать на хпр. Чаще всего требуется определять kU на шинах питания мощных тиристорных преобразователей. Под преобразователем подразумеваются выпрямительный мост (или их группа) и питающий понижающий трансформатор.
В этом случае хпр равно сопротивлению преобразовательного трансформатора и определяется по формуле [2]:
(4)
где Sном,Т — номинальная мощность преобразовательного трансформатора;
kp— коэффициент расщепления обмоток этого трансформатора;
uк% — сквозное напряжение КЗ трансформатора, приведенное к полной номинальной мощности трансформатора.
Для двухобмоточных трансформаторов, применяемых в шестифазных (трехфазных мостовых) схемах выпрямления, kp=0, трехобмоточных трансформаторов, применяемых в преобразователях, выполненных по двенадцатифазной схеме, в общем виде
где uК(НН1-НН2) — напряжение КЗ между вторичными обмотками трансформатора.
В общем случае для трансформаторов с расщепленными обмотками kр=0-4, если ветви низшего напряжения трансформатора имеют хорошую электромагнитную связь друг с другом, kр=0; если обмотки НН не имеют магнитной связи друг с другом или преобразователь выполнен по схеме с двумя трансформаторами, имеющими разные схемы соединения, то kр=4.
Действующее значение высшей гармоники напряжения в любой точке питающей сети при работе преобразователя с любой последовательностью чередования фаз выпрямления может быть определено по формуле [2]:
(5)
где 
- угол коммутации, рад.
Действующее значение тока любой гармоники в цепи преобразователя определяется из выражения [2]:
(6)
При работе группы вентильных преобразователей порядок расчета kU следующий. По приведенным формулам определяются уровни высших гармоник напряжения для каждого преобразователя.
Одинаковые гармоники напряжения всех преобразователей геометрически суммируются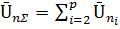 
. Затем определяется коэффициент несинусоидальности:
Особое внимание необходимо обращать на количество учитываемых гармоник, чтобы избежать ошибки в вычислении kU. Чем больше количество преобразователей и фаз выпрямления, тем большее количество гармоник необходимо учитывать. Предлагается следующая эмпирическая формула:
p=nmax=4qm+l, (7)
где nmax—наибольшая гармоника;
q — число работающих преобразователей;
m — число фаз выпрямления.
Для вентильного выпрямителя рассчитаем коэффициенты n-ой гармонической составляющей напряжения и коэффициент несинусоидальности на шинах 6 кВ.
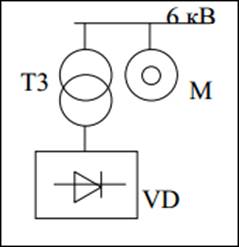
Исходные данные:
С: Sкз,6=170 МВА
Т3: SТ3=10 МВА; Uном=6 кВ; uк,%=10,5%
VD: Sпр=8 МВА; cos φ=0,8; m=6
М: РМ=280 кВт; cos φ=0,9; Км=1,2; К1=5,1
Считаем сопротивление преобразователя по формуле (4):
= 
где kр – коэффициент расщепления обмоток (для двухобмоточного трансформатора равен 0).
Сопротивление системы 
Коэффициент несинусоидальности по упрощенной формуле (2):
%
Согласно [1] допустимый коэффициент несинусоидальности для напряжения 6 кВ составляет 5%. Так как расчетный коэффициент больше допустимого, необходима установка фильтрующих устройств.
Согласно [2] для вентильных преобразователей необходимо учитывать в расчетах только 5, 7, 11, 13 гармоники.
Угол коммутации в радианах:
где m – число фаз преобразователя.
Напряжения высших гармоник и коэффициенты n-ной гармонической составляющей по (5) и (3)
| 
|
| 
|
| 
|
| 
|
| 
|
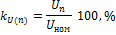
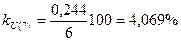
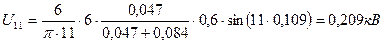
Искажения питающего тока и напряжения возникают за счет нелинейной характеристики дуги и за счет нелинейной характеристики трансформатора, работающего при повышенных значениях магнитной индукции. Уровень высших гармоник тока при работе сравнительно невелик, особенно по сравнению с высшими гармониками, генерируемыми вентильными преобразователями. Однако с ними следует считаться, так как мощность постоянно растет.
На основании экспериментальных исследований [2] получено соотношение для определения максимальных значений уровней отдельных гармоник тока при работе.
(8)
где Iт — ток трансформатора в расчетном режиме (для расчета максимальных значений гармоник надо брать в расчет номинальный ток трансформатора); n=2, 3, 4, 5...— номер соответствующей гармоники. Из соотношения видно, что достаточно в расчетах учитывать только до 7-й гармоники, так как остальные гармоники малы.
Для группы оборудования разной мощности
(9)
где Sn,Ti — мощность i-го трансформатора; Sn,Tmax — наибольшая мощность трансформатора в группе оборудования; In,max - ток n-oй гармоники трансформатора наибольшей мощности; N —общее число работающих трансформаторов.
Для определения kU в соответствующей точке сети необходимо определить уровни напряжения отдельных гармоник, генерируемых ДСП. Фазное напряжение гармоники в расчетной точке питающей сети находится из выражения
(10)
где In —действующее значение фазного тока n-oй гармоники; n —порядковый номер гармоники; Uном — номинальное линейное напряжение в расчетной точке; SК — мощность КЗ в расчетной точке.
Общий коэффициент несинусоидальности в расчетной точке при работе оборудования, %
(11)
где Uном — номинальное напряжение основной частоты в расчетной точке
Рассчитаем коэффициенты n-ой гармонической составляющей напряжения и коэффициент несинусоидальности на шинах 110 кВ.
Исходные данные:
С: Sкз,110 = 1900 МВА
Т2: SТ2=50 МВА; Uном=110 кВ
Считаем номинальный ток трансформатора
Согласно [2] в практических расчетах учитываются гармоники со 2-ой по 7-ю.
Токи, напряжения высших гармоник и коэффициенты n-ой гармонической составляющей напряжения рассчитываем по формулам (8), (10) и (3), где n –номер гармоники
|  , [кВ]
| 
|
| 
| 
|
| 
|  
|
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
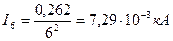
Коэффициент несинусоидальности напряжения на шинах 110 кВ
Согласно [1] допустимый коэффициент несинусоидальности для напряжения 110 кВ составляет 2%. Так как расчетный коэффициент не превышает допустимый, установка фильтрующих устройств на шины 110 кВ не требуется.