Доказательство
Пусть дан (n, m)-граф G. Предположим противное: все его вершины имеют разную степень.
Максимальная степень вершины в графе порядка n может быть равна (n -1), тогда вершины должны иметь степени (n -1), (n -2), …, 2, 1, 0. Но вершина степени (n -1) соединена со всеми оставшимися вершинами, в том числе и с изолированной, что невозможно. Пришли к противоречию, поэтому в любом графе обязательно найдутся две вершины, имеющие одинаковую степень. максимальная степень вершины может быть на единицу меньше количества вершин!!!!!!
1.3 Теорема о вершинах степени 0 или n-1
Пусть натуральные числа n и d,среди которых есть чётное удовлетворяют неравенствам 0<=d<=n-1.Тогда существует регулярный граф порядка n и степени d
1.4 Изоморфизм графов
Пусть G=(VG,EG) и H=(VH,EH) графы,где отображение a: VG ->VH биекция
.Если для любых вершин u и v графа G их образы а(u) и а(v) смежны в Н тогда и только тогда когда u и v смежны в G,то графы G и H изоморфны
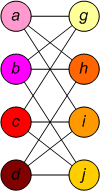

1.5 Матричное представление графов.
Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента aij равно числу рёбер из i -й вершины графа в j -ю вершину.
Иногда, особенно в случае неориентированного графа, петля (ребро из i -й вершины в саму себя) считается за два ребра, то есть значение диагонального элемента aii в этом случае равно удвоенному числу петель вокруг i -й вершины.
Матрица смежности простого графа (не содержащего петель и кратных рёбер) является бинарной матрицей и содержит нули на главной диагонали.
Проще говоря это симметрическая матрица с нулями на диагонали(если отсутствуют петли) число едениц в строке равно числу рёбер инцедентных соответствующей вершине. Теорема графы изоморфны тогда и только тогда,когда их матрицы смежности получаются друг из друга перестановками строк и столбцов следующим образом: Одновременно с перестановкой i-й и j-й строк переставляются i-й j-й столбцы. Из этой теоремы следует,что ранги матриц смежности изоморфных графов равны.
Определение. Матрицей инцедентности помеченного (n,m) – графа G=(VG,EG), где VG ={v1,v2,…..vn},EG ={e1,e2,…..en }называется NXM матрица,такая, что aij=1,если вершина vi и ребро ej инцедентны и aij=0 если вершина vi и ребро ej неинцедентны.В Каждом столбце матрицы инцедентности ровно две еденицы,равных столбцов нет. Теорема графы изоморфны тогда и только тогда когда их матрицы инцедентности получаются друг из друга произвольными перестановками строк и столбцов.
Операции с графами
2.1 Удаление рёбер и вершин,добавление рёбер и вершин,отождествление вершин, расщипление вершин
Определение Граф H=(VH,EH) называется подграфом графа G=(VG,EG)
,если VH включено VG и EH включено EG





2.2 Объединение,пересечение,произведение графов



Гомеоморфизм графов ответ находится выше.
2.4 n-Мерные кубы как особый класс графов,Коды ГРЕЯ
Первое фото выше,второе фото.

Маршруты, цепи,циклы.

3.3 Теорема о связности дополнения графа
Для любого графа либо он сам, либо его дополнение – связный граф.
Доказательство
Возьмем произвольный граф  . Если он связный, то теорема очевидна. Пусть граф
. Если он связный, то теорема очевидна. Пусть граф  – несвязный. Покажем, что дополнение графа
– несвязный. Покажем, что дополнение графа  будет связным графом, то есть любые две его вершины
будет связным графом, то есть любые две его вершины  и
и  соединены маршрутом.
соединены маршрутом.
Если вершины  и
и  принадлежали в графе
принадлежали в графе  различным компонентам связности, то в дополнении графа
различным компонентам связности, то в дополнении графа  они будут соединены ребром, которое и будет являться маршрутом, их соединяющим.
они будут соединены ребром, которое и будет являться маршрутом, их соединяющим.
Если вершины  и
и  принадлежат одной и той же компоненте связности, то в дополнении к графу
принадлежат одной и той же компоненте связности, то в дополнении к графу  они будут соединены маршрутом
они будут соединены маршрутом  , где
, где  – произвольная вершина любой другой компоненты связности.
– произвольная вершина любой другой компоненты связности.
3.4 Теорема о простом цикле.
Всякий цыкл содержит простой цикл.
Доказательство
Выберем в графе минимальный по количеству рёбер цикл (он существует, потому что количество рёбер в любом цикле — натуральное число [1]). Предположим, что он не простой. Но тогда он содержит дважды одну и ту же вершину, т. е. содержит в себе цикл меньшего размера, что противоречит тому, что наш цикл минимальный. Таким образом, этот цикл — простой.
3.5 Признаки двудольности графа 1) Теорема Кёнига для того чтобы граф был двудольным необходимо и достаточно,чтобы он не содержал циклов нечётной длины. Следствие для двудольности графа необходимо и достаточно чтобы он не содержал простых циклов нечётной длины. 2) Граф разбивается на пары разноцветных вершин тогда и только тогда, когда любые k элементов одной из долей связаны по крайней мере с k элементами другой(Теорема о свадьбах)
|
Пояснения к доказательству
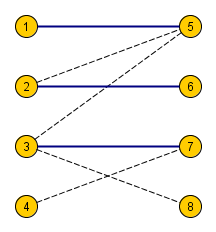

Пример
Пусть было построено паросочетание размером  (синие ребра).
(синие ребра).
Добавляем вершину с номером  .
.
Во множество  вошли вершины с номерами
вошли вершины с номерами 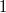 ,
,  ,
,  ,
,  ,
, 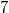 ,
,  .
.
Ненасыщенная вершина из правой доли всегда найдется (в примере вершина с номером  ), т.к иначе получаем противоречие:
), т.к иначе получаем противоречие:
- В
 входят только насыщенные вершины.
входят только насыщенные вершины. -
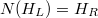
- В
 по крайней мере
по крайней мере  вершин (соседи по паросочетанию для каждой вершины из
вершин (соседи по паросочетанию для каждой вершины из  и ещё одна вершина, которую пытаемся добавить).
и ещё одна вершина, которую пытаемся добавить).
Цепь  является удлиняющей для текущего паросочетания.
является удлиняющей для текущего паросочетания.
Увеличив текущее парасочетание вдоль этой цепи, мы насытим вершину с номером  .
.

 Очевидно, что если существует полное паросочетание, то для любого
Очевидно, что если существует полное паросочетание, то для любого  выполнено
выполнено  . У любого подмножества вершин есть по крайней мере столько же соседей (соседи по паросочетанию).
. У любого подмножества вершин есть по крайней мере столько же соседей (соседи по паросочетанию).
 В обратную сторону докажем по индукции (будем добавлять в изначально пустое паросочетание
В обратную сторону докажем по индукции (будем добавлять в изначально пустое паросочетание  по одному ребру и доказывать, что мы можем это сделать, если
по одному ребру и доказывать, что мы можем это сделать, если  соединена хотя бы с одной вершиной из
соединена хотя бы с одной вершиной из  . Следовательно база верна.
Индукционный переход
Пусть после
. Следовательно база верна.
Индукционный переход
Пусть после  шагов построено паросочетание
шагов построено паросочетание  из
из  . Тогда в
. Тогда в  из
из  . Тогда существует путь из
. Тогда существует путь из 











 где последнее это есть минимальная степень вершины графа
где последнее это есть минимальная степень вершины графа . Если ребра есть, то несвязный граф получаем из данного, удаляя все ребра, инцидентные вершине с наименьшей степенью. В любом случае
. Если ребра есть, то несвязный граф получаем из данного, удаляя все ребра, инцидентные вершине с наименьшей степенью. В любом случае  .
.  .
.  . В последнем случае
. В последнем случае  , поскольку или граф
, поскольку или граф  .
.  ребер, удаление которых делает его несвязным. Ясно, что удаляя
ребер, удаление которых делает его несвязным. Ясно, что удаляя  ребер из этого множества получаем граф, имеющий мост
ребер из этого множества получаем граф, имеющий мост  . Для каждого из этих
. Для каждого из этих  и
и  . Удаление выбранных вершин приводит к удалению
. Удаление выбранных вершин приводит к удалению  ; если же он связен, то в нем есть мост
; если же он связен, то в нем есть мост  .
.


 и
и  - различные блоки графа
- различные блоки графа  . Рассмотрим подграф
. Рассмотрим подграф  . Он не является блоком, следовательно, или несвязен, или имеет шарнир. Если
. Он не является блоком, следовательно, или несвязен, или имеет шарнир. Если  несвязен, то
несвязен, то  - шарнир в
- шарнир в  принадлежит более чем одному блоку, то она инцидентна двум ребрам,
принадлежит более чем одному блоку, то она инцидентна двум ребрам, 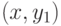 и
и  , принадлежащим разным блокам, то есть не являющимся циклически связанными. Но тогда всякий путь, соединяющий
, принадлежащим разным блокам, то есть не являющимся циклически связанными. Но тогда всякий путь, соединяющий  и
и  , проходит через
, проходит через 
 — плоский граф. Если добавить на нужных ребрах вершины степени
— плоский граф. Если добавить на нужных ребрах вершины степени  и удалить некотрые вершины степени
и удалить некотрые вершины степени  . Таким образом, доказательство достаточности следует из непланарности
. Таким образом, доказательство достаточности следует из непланарности  и
и  .
.
 .
База индукции, когда
.
База индукции, когда  , выполняется тривиальным образом. Предположим, что графы с любым числом вершин меньше
, выполняется тривиальным образом. Предположим, что графы с любым числом вершин меньше 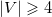 , мы можем нарисовать требуемым образом. Рассмотрим ребро
, мы можем нарисовать требуемым образом. Рассмотрим ребро  , инцидентное внутренней вершине глубочайшего разделяющего треугольника, то есть такого, который не содержит внутри себя других разделяющих треугольников. Если в графе нет разделяющих треугольников, то возьмём любое ребро. Тогда
, инцидентное внутренней вершине глубочайшего разделяющего треугольника, то есть такого, который не содержит внутри себя других разделяющих треугольников. Если в графе нет разделяющих треугольников, то возьмём любое ребро. Тогда  и
и  .
.
 Так как мы взяли вершины внутри самого глубого разделяющего треугольника, то у вершин
Так как мы взяли вершины внутри самого глубого разделяющего треугольника, то у вершин 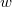 может быть только два общих соседа
может быть только два общих соседа 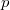 и
и  . Пусть
. Пусть 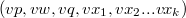 и
и 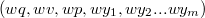 — обход по часовой стрелке ребер, исходящих соостветсвенно из
— обход по часовой стрелке ребер, исходящих соостветсвенно из  — граф, полученный из
— граф, полученный из  . Заменим пары параллельных ребер
. Заменим пары параллельных ребер 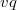 и
и  на
на  и
и  на
на  . Получим вершину
. Получим вершину  — по часовой стрелке.
— по часовой стрелке.
 Мы получили граф
Мы получили граф 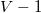 , то есть его можно уложить на плоскости требуемым образом: все ребра прямые (и сохранен обход по часовой стрелке ребер, инцидентных
, то есть его можно уложить на плоскости требуемым образом: все ребра прямые (и сохранен обход по часовой стрелке ребер, инцидентных  обозначим
обозначим  — круг радиуса
— круг радиуса  , с вершиной
, с вершиной  вершины
вершины  объединение всех отрезков, проведённых из
объединение всех отрезков, проведённых из  Тогда получим, что все соседи
Тогда получим, что все соседи 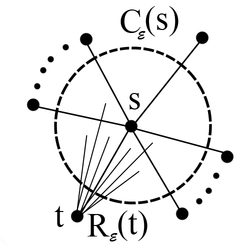 Проведем линию
Проведем линию  и
и  не лежало на
не лежало на  Удалим
Удалим  Получим, что
Получим, что 
