Рассмотрим два случая проявления центробежной силы инерции.
Случай 1. Рассмотрим вращающийся диск с закрепленными на нем стойками с шариками, подвешенными на нитях (рис.2). При вращении диска с постоянной угловой скоростью w шарики отклоняются на некоторый угол, тем больший, чем дальше он находится от оси вращения. Относительно инерциальной системы отсчета (неподвижной) все шарики движутся по окружности соответствующего радиуса R, при этом на шарики действует результирующая сила 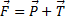 (рис.3).
(рис.3).
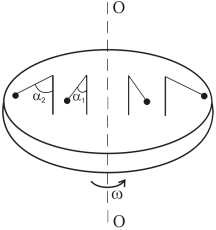
Рис.2
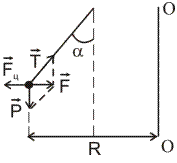
Рис.3
Согласно второму закону Ньютона
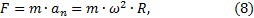
учитывая, что F / P =tgα, можно записать
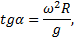
т.е. угол отклонения шарика зависит от угловой скорости и от его удаления от оси вращения диска.
Относительно неинерциальной системы отсчета, связанной с вращающимся диском, шарик находится в покое.
Это возможно в том случае, если сила 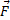 (8) уравновешена силой инерции
(8) уравновешена силой инерции 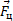 , называемой центробежной силой инерции:
, называемой центробежной силой инерции:
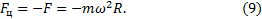
Случай 2. Рассмотрим диск, вращающийся вокруг перпендикулярной к нему вертикальной оси z с угловой скоростью ω. Вместе с диском вращается надетый на тонкую спицу шарик, соединенный с центром диска пружиной (рис. 4).
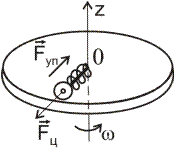
Рис.4
Шарик занимает на стержне некоторое положение, при котором сила натяжения пружины 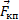 (она будет центростремительной) оказывается равной произведению массы шарика m на его ускорение:
(она будет центростремительной) оказывается равной произведению массы шарика m на его ускорение:

где 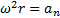 – нормальное ускорение на шарике; r – расстояние от оси вращения до центра шарика.
– нормальное ускорение на шарике; r – расстояние от оси вращения до центра шарика.
Относительно системы отсчета, связанной с диском, шарик покоится. Это формально можно объяснить тем, что кроме силы упругости на шарик действует сила инерции, модуль которой равен силе упругости (7):

Сила инерции 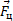 направлена вдоль радиуса от центра диска. Силу инерции (8), возникающую в равномерно вращающейся системе отсчета, называют центробежной силой инерции. Эта сила действует на тело во вращающейся системе отсчета, независимо от того, покоится тело в этой системе или движется относительно нее со скоростью
направлена вдоль радиуса от центра диска. Силу инерции (8), возникающую в равномерно вращающейся системе отсчета, называют центробежной силой инерции. Эта сила действует на тело во вращающейся системе отсчета, независимо от того, покоится тело в этой системе или движется относительно нее со скоростью 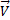 . Если положение тела во вращающейся системе отсчета характеризовать радиус-вектором
. Если положение тела во вращающейся системе отсчета характеризовать радиус-вектором 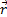 , то центробежную силу можно представить в виде
, то центробежную силу можно представить в виде
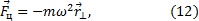
где 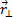 – компонента радиус-вектора, направленная перпендикулярно оси вращения.
– компонента радиус-вектора, направленная перпендикулярно оси вращения.
Центробежные силы, как и всякие силы инерции, существуют только в ускоренно движущихся (вращающихся) системах отсчета и исчезают при переходе к инерциальным системам отсчета.
Действию центробежной силы подвергается, например, пассажир в движущемся автобусе на поворотах. Если в центробежной машине подвесить на нитях несколько шариков и привести машину в быстрое вращение, то центробежные силы инерции отклонят шарики от оси вращения. Угол отклонения тем больше, чем дальше шарик отстоит от оси. Центробежные силы используются в центробежных сушилках для отжима белья, в сепараторах для отделения сливок от молока, в центробежных насосах, центробежных регуляторах и т.д. Их надо учитывать при проектировании быстровращающихся деталей механизмов.
Сила Кориолиса.
При движении тела относительно вращающейся системы отсчета, кроме центробежной силы, появляется еще одна сила, называемая силой Кориолиса.
Рассмотрим рис.5. Шарик массой m движется прямолинейно со скоростью 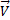 от центра к краю диска. Если диск неподвижен, то шарик попадает в точку М, а если диск вращается с постоянной угловой скоростью ω, то шарик попадает в точку N. Это обусловлено тем, что на шарик действует сила Кориолиса.
от центра к краю диска. Если диск неподвижен, то шарик попадает в точку М, а если диск вращается с постоянной угловой скоростью ω, то шарик попадает в точку N. Это обусловлено тем, что на шарик действует сила Кориолиса.
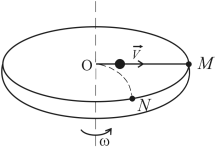
Рис.5
Появление силы Кориолиса можно обнаружить, если рассмотреть пример с шариком на спице на вращающемся диске, но без пружины. Для того чтобы заставить шарик двигаться с некоторой скоростью 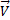 вдоль спицы, необходима боковая сила. Шарик вращается вместе с диском с постоянной угловой скоростью w, поэтому его момент импульса равен:
вдоль спицы, необходима боковая сила. Шарик вращается вместе с диском с постоянной угловой скоростью w, поэтому его момент импульса равен:
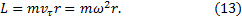
Если шарик будет перемещаться вдоль спицы с постоянной скоростью 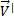 , то с изменением
, то с изменением 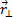 момент импульса шарика изменится. А это означает, что на движущееся во вращающейся системе тело должен действовать некоторый момент силы, который согласно основному уравнению динамики вращательного движения равен
момент импульса шарика изменится. А это означает, что на движущееся во вращающейся системе тело должен действовать некоторый момент силы, который согласно основному уравнению динамики вращательного движения равен
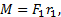
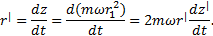
Для того чтобы заставить шарик двигаться по вращающемуся диску вдоль радиальной прямой со скоростью 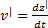 , необходимо прилагать боковую силу
, необходимо прилагать боковую силу
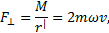
направленную перпендикулярно 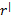 . Относительно вращающейся системы (диска) шарик движется с постоянной скоростью.
. Относительно вращающейся системы (диска) шарик движется с постоянной скоростью.
Это можно объяснить тем, что сила 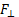 уравновешивается приложенной к шарику силой инерции
уравновешивается приложенной к шарику силой инерции 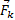 , перпендикулярной к скорости
, перпендикулярной к скорости 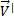 (рис.6). Сила
(рис.6). Сила 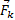 и есть Кориолисова сила инерции. Она определяется выражением
и есть Кориолисова сила инерции. Она определяется выражением
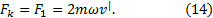
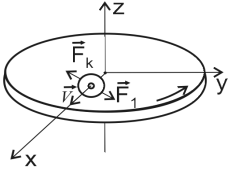
Рис.6
С учетом направления силу Кориолиса 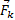 можно представить в виде
можно представить в виде
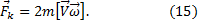
Сила Кориолиса всегда перпендикулярна скорости тела 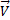 . Во вращающейся системе отсчета при
. Во вращающейся системе отсчета при 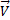 = 0 эта сила отсутствует. Таким образом, Кориолисова сила инерции возникает только тогда, когда система отсчета вращается, а тело движется относительно этой системы. Действием силы Кориолиса объясняется ряд эффектов, наблюдающихся на поверхности Земли, например, поворот плоскости колебаний маятника Фуко относительно Земли, отклонение к востоку от линии отвеса свободно падающих тел, размытие правого берега рек в северном полушарии и левого в южном, неодинаковый износ рельсов при двухколейном движении.
= 0 эта сила отсутствует. Таким образом, Кориолисова сила инерции возникает только тогда, когда система отсчета вращается, а тело движется относительно этой системы. Действием силы Кориолиса объясняется ряд эффектов, наблюдающихся на поверхности Земли, например, поворот плоскости колебаний маятника Фуко относительно Земли, отклонение к востоку от линии отвеса свободно падающих тел, размытие правого берега рек в северном полушарии и левого в южном, неодинаковый износ рельсов при двухколейном движении.
Принцип Даламбера.
Все методы решения задач динамики, которые мы до сих пор рассматривали, основываются на уравнениях, вытекающих или непосредственно из законов Ньютона, или же из общих теорем, являющихся следствиями этих законов. Однако, этот путь не является единственным. Оказывается, что уравнения движения или условия равновесия механической системы можно получить, положив в основу вместо законов Ньютона другие общие положения, называемые принципами механики. В ряде случаев применение этих принципов позволяет, как мы увидим, найти более эффективные методы решения соответствующих задач. В этой главе будет рассмотрен один из общих принципов механики, называемый принципом Даламбера.
Пусть мы имеем систему, состоящих из n материальных точек. Выделим какую-нибудь из точек системы с массой 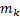 . Под действием приложенных к ней внешних и внутренних сил
. Под действием приложенных к ней внешних и внутренних сил 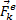 и
и 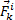 (в которые входят и активные силы, и реакции связи) точка получает по отношению к инерционной системе отсчета некоторое ускорение
(в которые входят и активные силы, и реакции связи) точка получает по отношению к инерционной системе отсчета некоторое ускорение 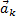 .
.
Введем в рассмотрение величину
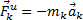 ,
,
имеющую размерность силы. Векторную величину, равную по модулю произведению массы точки на ее ускорение и направленную противоположно этому ускорению, называют силой инерции точки (иногда даламберовой силой инерции).
Тогда оказывается, что движение точки обладает следующим общим свойством: если в каждый момент времени к фактически действующим на точку силам 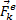 и
и 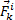 прибавить силу инерции
прибавить силу инерции 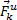 , то полученная система сил будет уравновешенной, т.е. будет
, то полученная система сил будет уравновешенной, т.е. будет
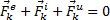 .
.
Это выражение выражает принцип Даламбера для одной материальной точки. Нетрудно убедиться, что оно эквивалентно второму закону Ньютона и наоборот. В самом деле, второй закон Ньютона для рассматриваемой точки дает 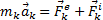 . Перенося здесь член
. Перенося здесь член 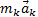 в правую часть равенства и придем к последнему соотношению.
в правую часть равенства и придем к последнему соотношению.
Повторяя проделанные высшее рассуждения по отношению к каждой из точек системы, придем к следующему результату, выражающему принцип Даламбера для системы: если в любой момент времени к каждой из точек системы, кроме фактически действующих на ней внешних и внутренних сил, приложить соответствующие силы инерции, то полученная система сил будет находиться в равновесии и к ней можно будет применять все уравнения статики.
Значение принципа Даламбера состоит в том, что при непосредственном его применении к задачам динамики уравнения движения системы составляются в форме хорошо известных уравнений равновесия; что делает единообразный подход к решению задач и обычно намного упрощает соответствующие расчёты. Кроме того, в соединении с принципом возможных перемещений, который будет рассмотрен в следующей главе, принцип Даламбера позволяет получить новый общий метод решения задач динамики.
Применяя принцип Даламбера, следует иметь в виду, что на точку механической системы, движение которой изучается, действуют только внешние и внутренние силы 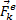 и
и 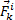 , возникающие в результате взаимодействия точек системы друг с другом и с телами, не входящими в систему; под действием этих сил точки системы и движутся с соответствующими ускорениями
, возникающие в результате взаимодействия точек системы друг с другом и с телами, не входящими в систему; под действием этих сил точки системы и движутся с соответствующими ускорениями 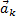 . Силы же инерции, о которых говорится в принципе Даламбера, на движущиеся точки не действуют (иначе, эти точки находились бы в покое или двигались без ускорений и тогда не было бы и самих сил инерции). Введение сил инерции - это лишь приём, позволяющий составлять уравнения динамики с помощью более простых методов статики.
. Силы же инерции, о которых говорится в принципе Даламбера, на движущиеся точки не действуют (иначе, эти точки находились бы в покое или двигались без ускорений и тогда не было бы и самих сил инерции). Введение сил инерции - это лишь приём, позволяющий составлять уравнения динамики с помощью более простых методов статики.
Из статики известно, что геометрическая сумма сил, находящихся в равновесии, и сумма их моментов относительно любого центра О равны нулю, причём по принципу отвердевания это справедливо для сил, действующих не только на твёрдое тело, но и на любую изменяемую систе6му. Тогда на основании принципа Даламбера должно быть:
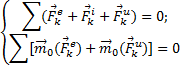
Введём обозначения:
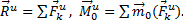
Величины 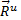 и
и 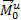 представляют собой главный вектор и главный момент относительно центра О системы сил инерции. В результате, учитывая, что геометрическая сумма внутренних сил и сумма их моментов равны нулю, получим из равенств:
представляют собой главный вектор и главный момент относительно центра О системы сил инерции. В результате, учитывая, что геометрическая сумма внутренних сил и сумма их моментов равны нулю, получим из равенств:
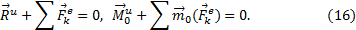
Применение уравнений (16), вытекающих из принципа Даламбера, упрощает процесс решения задач, т.к. эти уравнения не содержат внутренних сил.
В проекциях на оси координат эти равенства дают уравнения, аналогичные соответствующим уравнениям статики. Чтобы пользоваться этими уравнениями при решении задач, надо знать выражение главного вектора и главного момента сил инерций.
Пример 1. При каком минимальном значении скорости тяжелый шарик пройдет высшую точку петли радиуса R, не отрываясь от нее (рис.6.1)? Петля расположена в вертикальной плоскости.
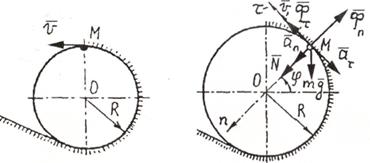
Рис.6.1
Решение. Будем считать шарик материальной точкой в промежуточном положении на его траектории. Приложим к шарику силу тяжести mg, нормальную реакцию петли 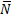 , касательную и нормальную силы инерции
, касательную и нормальную силы инерции 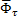 ,
, 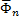 .
.
Согласно принципу Даламбера для точки получим уравновешенную в любой момент времени систему сил
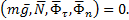
Проектируя эту систему сил на главную нормаль Mn получим
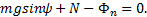
где Фn = man, аn = v2/R - нормальное ускорение шарика, (v — скорость шарика).
По условию задачи при ψ = 90° нормальная реакция в верхней точке петли N = 0, то есть
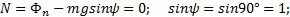
Отсюда
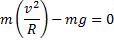
Скорость шарика
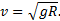
Пример 2. Однородный стержень АВ длиной l и массой т, закрепленный шарнирно на валу OO 1 вращается вокруг оси Оу с постоянной угловой скоростью ω (рис.6.2). Стержень удерживается под углом α к вертикали при помощи горизонтальной тяги BD. Найти реакции шарниров А и В.
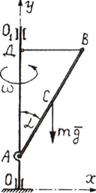
Рис.6.2
Решение. Применим для решения задачи принцип Даламбера. Приложим к стержню силу тяжести mg, составляющие реакции 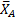 и
и 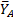 шарнира А вдоль осей координат, реакцию
шарнира А вдоль осей координат, реакцию 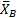 шарнира В (рис.6.3).
шарнира В (рис.6.3).
Силы инерции точек стержня заменим равнодействующей нормальной силой инерции 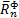 , приложенной в точке К, причем
, приложенной в точке К, причем
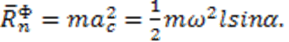
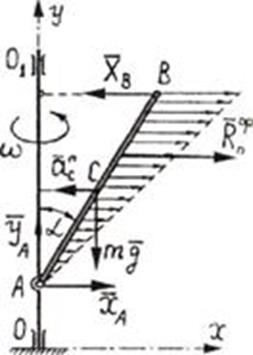
Рис.6.3
Получена уравновешенная в любой момент времени система сил
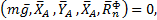
где 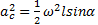 - нормальное ускорение центра масс стержня (точки С); АС= СВ.
- нормальное ускорение центра масс стержня (точки С); АС= СВ.
Условия мгновенного динамического равновесия стержня имеют вид
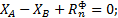
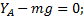
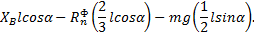
Из составленной системы уравнений с учетом значения силы 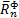 последовательно находим
последовательно находим
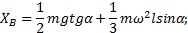
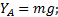
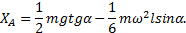
Пример 3. Однородный гладкий диск массы m и радиуса r установлен между валом OO1 и стержнем АВ, прикрепленным к нему под углом ѱ. Стержень и вал вращаются с постоянной угловой скоростью w вокруг оси Оу (рис.6.4). Определить давление диска на стержень и вал.
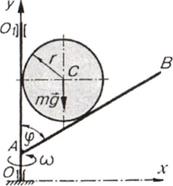
Рис.6.4
Решение. Воспользуемся принципом Даламбера.
Приложим к диску силу тяжести mg, реакцию вала 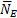 и реакцию стержня
и реакцию стержня 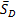 , а также равнодействующую нормальную силу инерции
, а также равнодействующую нормальную силу инерции 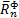 всех точек диска, причем
всех точек диска, причем
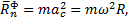
где 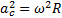 - нормальное ускорение центра масс диска (точки С).
- нормальное ускорение центра масс диска (точки С).
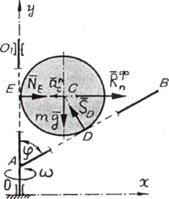
Рис.6.5
Сходящаяся система сил (mg, 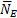 ,
, 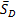 ,
, 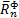 ) является уравновешенной в любой момент времени.
) является уравновешенной в любой момент времени.
Составим уравнения мгновенного динамического равновесия диска (указанной выше сходящихся системы сил)
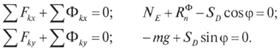
Из этой системы уравнений с учетом значения силы 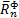 находим:
находим:
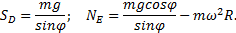
Давление диска на стержень и вал в точках В и D равны соответствующим реакциям стержня и вала
QD = SD; РЕ = NЕ.
Домашнее задание: