1. Строим дуги начальных окружностей, касающихся в точке Р – полюсе зацепления.
2. Через точку Р проводим прямую NN, образующую угол άw c общей касательной ТТ к начальным окружностям в точке Р.
3. Из центров О 1 и О 2 зубчатых колес опускаем на прямую NN перпендикуляры О 1 N 1 и О 2 N 2, являющиеся радиусами основных окружностей rb 1, rb 2, и строим основные окружности.
4. Строим эвольвенты, которые описывает точка Р прямой NN при перекатывании ее по основным окружностям как для первого, так и для второго колеса.
5. Проводим окружности впадин и вершин колес. Если радиус окружности впадин меньше радиуса основной окружности, то для получения полного зуба из начала эвольвенты на основной окружности проводим радиальный отрезок до окружности впадин. Это построение не дает действительного профиля зуба внутри основной окружности, а является чертежным приемом.
6. Проводим делительную окружность первого колеса. От точки
пересечения этой окружности с соответствующей эвольвентойоткладываем по делительной окружности вправо и влево дуги, равные шагу зацепления р ά. Затем определяем толщину зуба. На втором колесе построение аналогично.
7. Переходим к определению активной линии зацепления. Теоретически линией зацепления является отрезок N 1 N 2, касательный к основным окружностям, заключенный между точками касания. Активной линией зацепления является отрезок В 1 В 2 линии зацепления, заключенный между точками пересечения ее с окружностями вершин.
8. Определяем дугу зацепления. Для этого через крайние точки В 11 В 12 рабочего участка профиля зуба первого колеса проводим нормали к этому профилю, т.е. касательные к основной окружности первого колеса. Дуга а 1 b 1 начальной окружности, заключенная между точками а 1 и b 1 пересечения этих нормалей с начальной окружностью, является дугой зацепления первого колеса. Дугу зацепления а 2 b 2 для второго колеса находим аналогично. Дуги зацепления колес равны между собой и могут быть подсчитаны:
 а 1 b 1 =
а 1 b 1 = 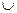 а 2 b 2 = B 1 B 2 / cos ά w
а 2 b 2 = B 1 B 2 / cos ά w
или определены графически. Для этого в конечных точках B 1, B 2 рабочей части линии зацепления восстанавливаем перпендикуляры и отмечаем точки их пересечения c общей касательной к начальным окружностям в точке Р. Отрезок ab касательной будет равен дуге зацепления.
9. После построения картины зацепления производим подсчёт коэффициента перекрытия по формуле
εα = 
где В 1 В 2 – данные из чертежа.
Одним из признаков правильного построения картины зубчатого зацепления является нахождение точек контакта зубьев на линии зацепления.
10. Подсчитываем значение коэффициентов удельных скольжений ν1 и ν2:
ν 1 = 1 – ((g – x)/ x) · U 2–1,
ν 1 = 1 –  · U 1–2.
· U 1–2.
Для этого длину g = N 1 N 2 измеряем по чертежу в миллиметрах, а значения Х берём в границах от 0 до g с интервалами 10–30 мм.
Пользуясь полученными значениями ν1, строим диаграммы коэффициентов ν1 и ν2.
Для этого проводим ОХ, параллельную линии зацепления N 1 N 2. Перпендикуляры N 1 O 1 и N 2 O 2 отсекают на прямой отрезок g, равный теоретической линии зацепления N 1 N 2. На оси ОХ откладываем значения х, а на прямых, параллельных N 1 O, принятой за ось ординат, для соответствующих значений х откладываем значения ν1 и ν2. Для выделения частей диаграмм, соответствующих значениям ν1 и ν2 рабочих участков профилей зубьев, восстанавливаем из точек b 1 и b 2 линии зацепления перпендикуляры. Для большей наглядности строим круговые диаграммы ν1 и ν2 непосредственно на профилях зубьев соответствующих колёс.
Построение круговых диаграмм производим следующим образом. С участка оси Ох прямоугольных диаграмм, соответствующих активной линии зацепления, сносим на линию зацепления N 1 N 2 ряд точек.
Затем из центра вращения колёс О 1 и О 2 через полученные на линии зацепления точки проводим дуги на соответствующие профили зубьев. Отложив на этих дугах от точек профилей отрезки, равные или пропорциональные ординатам прямоугольных диаграмм для соответствующих точек и колёс (для колеса 1 – ординаты Y 1, а для колеса 2 – Y 2) и соединив их плавной кривой, получим круговые диаграммы ν1 и ν2.
7.11. Порядок построения картины
инструментального зацепления
Для построения картины инструментального зацепления выбирают исходный контур зубчатой рейки, например по ГОСТу 16530-70, и определяют все размеры зубчатого колеса без смещения и со смещением по соответствующим формулам, приведенным в табл. 7.1. В настоящее время широко используют метод обкатки, применяя стандартный инструмент и сдвигая его на определенную величину от центра или к центру заготовки зубчатого колеса.
При нарезании зубчатого колеса без смещения режущего инструмента рейка располагается так, что ее модульная средняя линия совпадает с делительной прямой и касается окружности радиуса  нарезаемого колеса. При таком положении рейки толщина зуба колеса и ширина зуба рейки равны на модульной прямой.
нарезаемого колеса. При таком положении рейки толщина зуба колеса и ширина зуба рейки равны на модульной прямой.
При нарезании рейкой колеса со смещением по окружности радиуса  будет уже катиться не средняя модульная прямая, а делительная прямая, отстоящая от модульной прямой на величину смещения хт. Построение инструментального зацепления начинается с вычерчивания профиля инструментальной рейки. Для этого проводят среднюю линию рейки и от нее откладывают вверх и вниз расстояния, равные m и 1,25 m. На этих расстояниях вычерчивают прямые, параллельные средней линии. Далее среднюю линию рейки разбивают на ряд отрезков, равных половине шага, т.е. получают точки, через которые проводят боковые грани зубьев рейки под углом 20° к вертикали. Для нахождения центра Со дуги закругления головки инструмента необходимо выполнить обычные сопряжения пересекающихся прямых радиусом
будет уже катиться не средняя модульная прямая, а делительная прямая, отстоящая от модульной прямой на величину смещения хт. Построение инструментального зацепления начинается с вычерчивания профиля инструментальной рейки. Для этого проводят среднюю линию рейки и от нее откладывают вверх и вниз расстояния, равные m и 1,25 m. На этих расстояниях вычерчивают прямые, параллельные средней линии. Далее среднюю линию рейки разбивают на ряд отрезков, равных половине шага, т.е. получают точки, через которые проводят боковые грани зубьев рейки под углом 20° к вертикали. Для нахождения центра Со дуги закругления головки инструмента необходимо выполнить обычные сопряжения пересекающихся прямых радиусом  . Таким образом, получают 3–4 зуба инструментальной рейки. В случае нарезания нормального колеса касательная Р 5к делительной окружности должна совпадать со средней линией рейки (рис. 7.10). Если нарезается колесо со смещением, то делительная окружность его должна касаться делительной прямой рейки, отстоящей от средней рейки на величину смещения х 1 т (рис. 7.11).
. Таким образом, получают 3–4 зуба инструментальной рейки. В случае нарезания нормального колеса касательная Р 5к делительной окружности должна совпадать со средней линией рейки (рис. 7.10). Если нарезается колесо со смещением, то делительная окружность его должна касаться делительной прямой рейки, отстоящей от средней рейки на величину смещения х 1 т (рис. 7.11).
Значение коэффициента смещения х 1для малого колеса следует оставить прежним, т.е. таким, каким оно было выбрано раньше для вычерчивания картины зацепления колес. Следовательно, размеры малого колеса остаются прежними. В соответствии с вышеизложенным проводят

Рис. 7.10. Инструментально-реечное зацепление без смещения рейки

Рис. 7.11. Инструментально-реечное зацепление со смещением рейки
делительную прямую, отстоящую от средней линии рейки на величину смещения х 1 m в направлении, соответствующем положительному или отрицательному смещению инструмента. Через точку пересечения делительной прямой с профилем зуба рейки Р проводят вертикаль, на которой от точки Р откладывают отрезок РО 1, равный радиусу делительной окружности нарезанного колеса, т.е. получают его центр O 1и из него затем проводят все окружности. Построение эвольвенты производят изложенным ранее способом.
Переходная кривая, сопрягающая эвольвентную часть профиля зуба с окружностью впадин, образуется на станке автоматически как результат движения подачи скругленной части головки зуба инструментальной рейки относительно заготовки колеса.
Для построения относительных траекторий точек, лежащих на профиле рейки, сообщают заготовке и рейке движение с угловой скоростью –ω(угловая скорость колеса). Тогда колесо остановится, а делительная прямая рейки будет перекатываться без скольжения по делительной окружности колеса. Точки 1, 2, 3, 4 на делительной прямой рейке (см. рис. 7.10) будут совпадать с точками 1', 2', 3', 4, 5' на делительной окружности колеса (см. рис. 7.10). Указанные точки предварительно были получены путем откладывания равных отрезков длиной 5–10 мм на делительной окружности и делительной прямой рейки. Координаты центра дуги определяются в точке скругления головки зуба рейки  . Центр С 0дуги закругления головки инструмента при таком перекатывании опишет удлиненную эвольвенту. Эту эвольвенту строят так: соединяют точку С 0прямыми линиями с точками 1, 2, 3, 4, 5 и 1", 2", 3", 4", 5" и затем – названные точки между собой. В результате получают ряд треугольников (см рис. 7.10) – показан только один ∆ С 055").
. Центр С 0дуги закругления головки инструмента при таком перекатывании опишет удлиненную эвольвенту. Эту эвольвенту строят так: соединяют точку С 0прямыми линиями с точками 1, 2, 3, 4, 5 и 1", 2", 3", 4", 5" и затем – названные точки между собой. В результате получают ряд треугольников (см рис. 7.10) – показан только один ∆ С 055").
Для определения, например, положения точки С 5необходимо из центра 5' провести дугу радиусом С 05, а из центра О 1засечь эту дугу радиусом С 05 ". Точно так же определяются положения точек С 1, С 2, …, С 5,…. Соединив точки С 0, С 1, С 5,получают траекторию точки С 0.Если из найденных точек С 0, С 1, …, С 5построенной кривой провести дуги радиусом  , то огибающая этого семейства дуг и будет профилем ножки зуба.
, то огибающая этого семейства дуг и будет профилем ножки зуба.
Построение профиля ножки зуба при станочном зацеплении можно провести и другими методами, в частности упрощенным. Из точки 1 определяем радиус окружности касательной к головке рейки, а затем из точки 1' проводим дугу того же радиуса. Повторяем построение соответственно для точек 2 и 2', 3 и 3' и т.д. (рис. 7.10, 7.11).
Огибающая всех положений построенных дуг будет профилем ножки зуба.