По направлению проецирующих лучей различают проецирование центральное и параллельное.
Метод центрального (конического) проецирования заключается в том, что все проецирующие лучи, проходящие через точки пространства, исходят из одной точки S — центра проецирования (рис. 1).
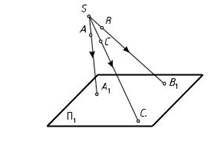
Рис. 1. Метод центрального проецирования
Метод параллельного проецирования основан на том, что центр проецирования S удален на бесконечно большое расстояние от плоскости проекций, и проецирующие лучи становятся параллельны между собой и некоторому заданному направлению проецирования N.
При параллельном проецировании различают: ортогональное (прямоугольное) проецирование, когда проецирующие лучи перпендикулярны плоскости проекций (рис. 2, а); косоугольное проецирование, когда проецирующие лучи не перпендикулярны плоскости проекций (рис. 2, б).
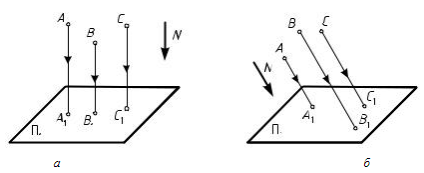
Рис. 2. Метод параллельного проецирования
Рассмотрим некоторые свойства параллельных проекций.
1. Проекция точки есть точка. Это очевидно из самого определения проекции точки как точки пересечения проецирующего луча
С плоскостью проекций.
2.Проекция прямой в общем случае прямая. Действительно, для построения проекции прямой АВ необходимо через каждую принадлежащую этой прямой точку провести проецирующий луч. Все проецирующие лучи, проходящие через точки прямой АВ, параллельны заданному направлению проецирования N. Совокупность этих лучей образует проецирующую или лучевую плоскость α, которая при пересечении с плоскостью проекцийП1 определяет проекцию прямой А 1 В 1:
| А 1 В 1|= α ∩ П1, | АВ | α.
В частном случае проекция прямой СD есть точка C 1 ≡ D 1 (рис. 3).
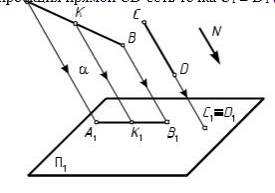
Рис. 3. Проекции прямых
3. Если точка пространства принадлежит прямой, то и проекция этой точки принадлежит проекции прямой (рис. 3). Это свойство следует непосредственно из определения проекции геометрической фигуры как множества проекций всех принадлежащих ей точек. Если точка K принадлежит прямой АВ и плоскости α, то и проецирующий луч, исходящий из точки K, принадлежит плоскости α. Следовательно, этот луч пересечет плоскость проекций П1 в линии пересечения плоскостей α и П1, т. е. в точке K1, принадлежащей проекции прямой А1В1:
K |AB| K1 |A1B1|.
4. Отношение отрезков прямой пространства равно отношению их проекций (рис. 3). Если точка K делит отрезок прямой пространства АВ в отношении m: n, то и проекция этой точки K1 делит в таком же отношении проекцию этого отрезка прямой А1В1:
| АK | = | А1K1 | = | m | . | ||||||||
| KB | K В | n | |||||||||||
| 1 | 1 |
В начертательной геометрии рассматривают следующие основные виды проекций: ортогональные; перспективные; аксонометрические; проекции с числовыми отметками.
При ортогональном проецировании каждой точке пространства соответствует одна и только одна проекция точки (рис. 4, а). Вместе с тем, каждой проекции точки соответствует множество точек пространства, расположенных на одном проецирующем луче (рис. 4, б).
Следовательно, одна проекция точки не определяет положения этой точки в пространстве. Для определения положения точки в пространстве необходимо иметь две ее проекции, полученные при двух различных направлениях проецирования.
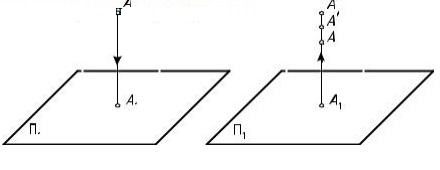
| а | б |
Рис. 4. Проецирование точки
Домашнее задание.
1. Кратко законспектировать материал на тему: «Методы проецирования. Терминология процесса проецирования».
2. Выучить материал из учебника Хаскин А.М. Черчение: учебник для техникумов/ А.М. Хаскин; Под ред. А.В. Блиока. - 3-е изд., перераб. и доп. - К.: Вища школа, 1979. - с.70-72.
3. Ответить на следующие вопросы:
3.1. В чем сущность центрального проецирования?
3.2. В чем сущность параллельного проецирования?
3.3. На какие виды разделяются параллельные проекции?