Перед началом реализации работы необходимо выделить необходимые задачи:
- Определиться с функционалом класса
- Разработать интерфейс класса
- Разработать интерфейс тестового приложения
- Реализовать проектное решение
- Исследовать одну из операций над элементами; построить зависимость времени выполнения операции от числа элементов, над которыми она выполняется
- Оценить асимптотическую сложность реализованных алгоритмов вставки, удаления и поиска элементов класса
ПРОЕКТИРОВАНИЕ
На этапе проектирования необходимо придумать, какие поля и методы будет включать в себя реализуемый класс. Помимо этого, важно, чтобы реализованный код мог быть простым в плане его доработки и модификации. То есть, если потребуется, в дальнейшем программист должен иметь возможность без труда определять в данном классе новые поля или методы, не изменяя при этом разработанный ранее класс. Жизненный цикл программы должен быть универсален.
Поля и методы класса представлен в табл. 2.1 и табл. 2.2 соответственно.
Таблица 2.1
Поля класса Tree
| Название поля | Назначение |
| root | Значение верхнего, корневого элемента дерева |
Таблица 2.2
Методы класса Tree
| Название метода | Назначение | |
| __init__(self) | Инициализация экземпляра класса Tree без установленного значения корневому элементу. Конструктор. | |
| insert(self,data) | Добавление в дерево узла с ключом data. Добавляемое значение может быть как целочисленным, так и вещественным. Объект добавления – экземпляр класса Node. | |
| search(self,data) | Поиск в дереве узла с ключом data. | |
| getHeight(self) | Вычисление высоты дерева – самого длинного пути от корневого узла вниз до внешнего узла поддерева. | |
| getSize(self) | Вычисление количества узлов в дереве. | |
| getTreeView(self) | Вывод структуры текущего дерева в консоль | |
| preorder(self) | Прямой обход бинарного дерева (корень, левый потомок, правый потомок). | |
| postorder(self) | Обратный обход бинарного дерева (левый потомок, правый потомок, корень). | |
| inorder(self) | Симметричный обход бинарного дерева (левый потомок, корень, правый потомок). | |
| remove(self,data) | Удаление узла с ключом data. | |
Можно заметить, что на данный момент есть класс только лишь с одним полем – корнем. Данный класс, на самом деле, позволяет нам всегда иметь доступ и понимание того, какой узел является корневым. Остальные узлы будут представлять из себя объекты класса Node, Функционал которого далее будет разобран.
Данный класс должен иметь поля, представленные в табл. 2.3.
Таблица 2.3
Поля класса Node
| Название поля | Назначение |
| value | Значение ключа узла |
| left | Левый потомок |
| right | Правый потомок |
Методы класса Node описаны в табл. 2.4
Таблица 2.4
Методы класса Node
| Название метода | Назначение |
| __init__(self, value) | Инициализация экземпляра класса Node, инициализация пустых полей left, right, и установка значения полю value. Конструктор. |
| insert(self,data) | Добавление в дерево узла с ключом data. Добавляемое значение может быть как целочисленным, так и вещественным. |
| search(self,data) | Поиск в дереве узла с ключом data. |
| getHeight(self) | Вычисление высоты дерева – самого длинного пути от корневого узла вниз до внешнего узла поддерева. |
| getSize(self) | Вычисление количества узлов в дереве. |
| getTreeView(self) | Вывод структуры текущего дерева в консоль |
| preorder(self) | Прямой обход бинарного дерева (корень, левый потомок, правый потомок). |
| postorder(self) | Обратный обход бинарного дерева (левый потомок, правый потомок, корень). |
| inorder(self) | Симметричный обход бинарного дерева (левый потомок, корень, правый потомок). |
Иерархия классов устроена таким образом, что при вызове метода у объекта класса Tree, происходит обращение к одноименному методу объекта класса Node.
Структура классов определена, но пока непонятно, как с ними взаимодействовать. Для этого необходимо разработать простой, понятный для пользователя консольный интерфейс. Данный интерфейс должен предоставлять все возможности для взаимодействия с классом. То есть, пользователь должен иметь следующие возможности:
- Создавать дерево
- Отображать дерево в консоли (в структурном виде, или методами прямого, симметричного или обратного обходов)
- Очищать дерево
- Добавлять узлы в дерево
- Удалять узлы в дереве
- Искать узлы в дереве
- Считать высоту дерева
- Считать размер узлов в дереве
- Выходить из программы
Итак, поскольку структура разрабатываемых классов и тестового приложения определены, можно приступить к реализации программного продукта.
КОДИРОВАНИЕ И ОТЛАДКА
МЕТОДЫКЛАССА NODE
Далее представлен список методов с пояснением их реализации:
· __init__(self, data) (Приложение А.1, стр. 2):
Конструктор класса Node. При его вызове поле value у данного объекта устанавливается значением data, а поля left и right – значением None.
· insert(self, data) (Приложение А.1, стр. 8):
Добавление узла в дерево. Принимает параметр data целочисленного или вещественного типа. Если data равно значению текущего узла, значит узел с таким значением уже существует, и метод возвращает значение False. Иначе идет проверка, меньше ли data значения value текущего узла. Если так, то идет рекурсивный вызов того же метода insert у левого потомка текущего узла, если он существует; если нет, то левый потомок становится объектом класса Node со значением data, метод возвращает результат True. Иначе та же логика, только с правым потомком. В итоге метод возвращает результат рекурсивно вызванных методов, а также, в успешном случае, присваивает значение объекта класса Node левому или правому потоку одного из узлов (поля left и right).
· search(self, data) (Приложение А.1, стр. 27):
Поиск узла в дереве. Принимает параметр data целочисленного или вещественного типа. Если data равно значению текущего узла, значит узел с таким значением найден, и метод возвращает значение True. Иначе идет проверка, меньше ли data значения value текущего узла. Если так, то идет рекурсивный вызов того же метода insert у левого потомка текущего узла, если он существует; если нет, значит узла со значением data в дереве нет, метод возвращает результат False. Иначе та же логика, только с правым потомком. В итоге метод возвращает результат рекурсивно вызванных методов.
· getSize(self) (Приложение А.1, стр. 42):
Определение количества узлов в дереве. Если у узла есть оба потомка, метод возвращает результат суммирования единицы, количества узлов у левого поддерева и количества узлов у правого поддерева. Количество узлов у потомков вычисляется путем вызова того же метода, getSize. Если у узла есть только левый потомок, метод возвращает результат суммирования единицы и количества узлов у левого поддерева. Если существует только правый – результат суммирования единицы и количества узлов у правого поддерева. Если нет ни правого, ни левого потомка, значит узел является листом, и метод возвращает результат 1. Последнее условие позволяет прерывать рекурсивный вызов метода getSize при достижении листьев.
· getHeight(self) (Приложение А.1, стр. 53):
Определение высоты дерева. Логика устроена по тому же принципу, что и метод getSize, однако в случае, когда существует и правый, и левый потомки, возвращается максимальная высота из двух поддеревьев плюс единица.
· getTreeView(self) (Приложение А.1, стр. 88):
Вывод структуры дерева в консоли. Если у узла есть потомки слева и справа, метод возвращает строку типа “ («getTreeView для левого потомка» «значение узла» «getTreeView для правого потомка») ”. Если есть только потомок слева, то метод возвращает строку типа “ («getTreeView для левого потомка» «значение узла» None) ”. Аналогично, если есть только потомок справа. Если же потомков нет то метод возвращает строку “ (None «значение узла» None) ”. Рекурсия прерывается при достижении листьев дерева.
· preorder(self) (Приложение А.1, стр. 64):
Прямой обход дерева с выводом значений узлов. Вывод значения узла, затем, если у узла есть потомок слева, происходит рекурсивный вызов метода preorder для левого поддерева. Далее то же самое, если у узла есть потомок справа.
· postorder(self) (Приложение А.1, стр. 72):
Обратный обход дерева с выводом значений узлов. Действия повторяют предыдущий метод preorder, однако сейчас происходит попытка рекурсивного вызова метода postorder для левого поддерева, затем для правого поддерева, и в конце вывод значения текущего узла.
· inorder(self) (Приложение А.1, стр. 80):
Симметричный обход дерева. Логика схожа с методами preorder и postorder, но теперь последовательность следующая: попытка обхода слева, вывод значения текущего узла, попытка обхода справа.
МЕТОДЫКЛАССА TREE
Далее представлен список методов с пояснением их реализации:
· __init__(self) (Приложение А.2, стр. 5):
Конструктор класса Tree. При его вызове поле root у данного объекта устанавливается значением None.
· insert(self, data) (Приложение А.2, стр. 8):
Добавление узла в дерево. Принимает параметр data целочисленного или вещественного типа. Если есть корневой узел, вызывается одноименный метод класса Node у объекта root. Иначе, вызывается конструктор класса Node, результат вызова присваивается полю root.
· search(self, data) (Приложение А.2, стр. 15):
Поиск узла со значением data. Принимает параметр data целочисленного или вещественного типа. Если root не имеет значение None, то вызывается одноименный метод у объекта root. Результат является возвращаемым значением. Если root имеет значение None, возвращается значение False.
· getHeight(self) (Приложение А.2, стр. 21):
Определение высоты дерева. Если root не имеет значение None, то вызывается одноименный метод у объекта root. Результат является возвращаемым значением. Если root имеет значение None, то есть в дереве нет узлов, возвращается значение 0.
· getSize(self) (Приложение А.2, стр. 27):
Определение количества узлов в дереве. Если root не имеет значение None, то вызывается одноименный метод у объекта root. Результат является возвращаемым значением. Если root имеет значение None, то есть в дереве нет узлов, возвращается значение 0.
· getTreeView(self) (Приложение А.2, стр. 33):
Вывод структуры дерева в консоли, если значение root не имеет значение None.
· preorder(self) (Приложение А.2, стр. 37):
Вызов одноименного метода у объекта root, если он не имеет значение None.
· postorder(self) (Приложение А.2, стр. 41):
Вызов одноименного метода у объекта root, если он не имеет значение None.
· inorder(self) (Приложение А.2, стр. 45):
Вызов одноименного метода у объекта root, если он не имеет значение None.
· remove(self, data) (Приложение А.2, стр. 49):
Удаление узла в дереве со значением data. Если поле root имеет значение None, метод возвращает результат False – дерево пустое, и ничего не было удалено. Дальше нужно проверить, искомый узел – корневой или нет. Если да, то рассматривается 4 случая: узел не имеет потомков, узел имеет только левого потомка, узел имеет только правого потомка, и узел имеет обоих потомков. В первых трех случаях значение логика описана в 1 действие. Больше внимания стоит уделить 4 случаю, когда есть и правый, и левый потомок. Необходимо найти узел с наименьшим значением, справа от root. Именно этот узел и станет корневым. Поэтому, сначала идет обращение к правому потомку корневого узла, а от него идет цикличный «спуск» к левому потомку, пока такие существуют. Теперь, необходимо изменить значение корневого узла на значение, определенное из предыдущей операции. Однако, перед этим, необходимо убрать связи с узлом, который станет корневым. А также учесть случай, где у узла нет левого, но есть правый потомок. Для этого идет проверка на наличие правого потомка у удаляемого узла. Если есть, то правый потомок становится левым или правым потомком у родительского узла, в зависимости от значения. Иначе, левый или правый потомок у родительского узла пропадает, то есть получает значение None, это зависит то того, какое значение было у перемещаемого узла. В конечном итоге, значение корневого узла обновляется, и метод возвращает результат True.
Теперь стоит рассмотреть ситуацию, когда удаляемый узел не является корневым. Для этого идет цикличный спуск по узлам в поисках нужного значения. Если узла с требуемым значением не удалось найти, метод возвращает результат False. Далее взаимодействие происходит примерно то же, что и с корневым узлом, однако, если у корневого узла родителя не существует, сейчас необходимо учитывать присутствие родительского узла. В итоге метод вернет значение True, что говорит об успешно выполненной операции.
ТЕСТИРОВАНИЕ
ИНТЕРФЕЙС ПРОГРАММЫ
На этапе тестирования разработчик должен удостовериться в том, что классы реализованы корректно и работа будет адекватной при любых, как часто используемых, так и частных случаях. Необходимо разработать удобный, понятный интерфейс для пользователя, и такой, чтобы пользователь мог адекватно пользоваться функционалом, в полной мере. Для этого требуется добавить кучу проверок перед вызовом различных методов класса, чтобы интерфейс сообщал о невозможности выполнения того или иного действия, а не прекращал работу. В конечном итоге был разработан консольный интерфейс, способный адекватно обрабатывать возможные ошибки со стороны пользователя и продолжать работу (рис 4.1.1).

Рисунок 4.1.1 – Главное меню
Дополнением было добавлена возможность создать случайное бинарное дерева путем обращения к 12 пункту. Будет создано дерево размером от 3 до 15 узлов, значения которых лежат в диапазоне [1; 100].
Рассмотрим, что происходит в каждом из подпунктов.
При создании дерева выскакивает диалоговое сообщение с просьбой задать значение корневого узла (рис. 4.1.2). Если пользователь введет нецелочисленное значение, программа сообщит об ошибке, и вернет пользователя в главное меню (рис. 4.1.3). Если входные данные успешно пройдут проверку, произойдет возврат в главное меню (рис. 4.1.4).
Рисунок 4.1.2 – Создание дерева. Задание корневого значения

Рисунок 4.1.3 – Создание дерева. Обработка неверных входных данных
Рисунок 4.1.4 – Создание дерева. Успешное добавление узла.
Если пользователь решит создать дерево, когда у него оно уже существует, программа сообщит об ошибке (рис. 4.1.5).
Рисунок 4.1.5. Создание дерева. Проверка на существование.
Далее вторым пунктом пользователь может посмотреть, как выглядит структура бинарного дерева на данный момент (рис. 4.1.6). На данный момент существует дерево с единственным узлом со значением 20. Потомков нет ни слева, ни справа, поэтому в консоли отображены значения None. Круглые скобки позволяют отображать связь между узлами и создавать эффект вложенности. Если дерево не было создано перед обращением к данной функции, будет отображено сообщение об ошибке (рис. 4.1.7). На самом деле, проверка на существование дерева происходит во всех пунктах, кроме нулевого.

Рисунок 4.1.6 – Отображение текущей структуры бинарного дерева.
Третий пункт позволяет очистить дерево. Если дерево пустое или не создано, пользователю сообщается об ошибке. Иначе дерево очищается, и его необходимо создать путем вызова 1 пункта меню.
Пункт под номером 4 запрашивает от пользователя значение, которое он хочет добавить в дерево, если оно было создано ранее (рис. 4.1.7). Если попытаться добавить узел с уже существующим значением, программа сообщит об этом (рис. 4.1.8).
Рисунок 4.1.7 – Добавление узла в бинарного дерево
Рисунок 4.1.8 – Добавление узла с аналогичным значением
Пятый пункт позволяет удалить узел в дереве. Если введенного значения нет в дереве, пользователь получает сообщение об ошибке (рис. 4.1.9). Иначе пользователь возвращается в меню.
Рисунок 4.1.9 – Удаление узла с несуществующим значением
Шестой пункт работает аналогично предыдущему: пользователь получает сообщение, найден (рис. 4.1.10) или не найден (рис. 4.1.11) запрошенный узел.
Рисунок 4.1.10 – Удачный поиск
Рисунок 4.1.11 – Неудачный поиск
Седьмой пункт показывает пользователю, какая высота у текущего дерева, если оно было создано ранее (рис. 4.1.12).
Рисунок 4.1.12 – Высота бинарного дерева
Восьмой пункт показывает пользователю размер текущего дерева, если оно существует (рис. 4.1.13).
Рисунок 4.1.13 – Размер бинарного дерева
В пунктах 9, 10 и 11 происходит вывод элементов бинарного дерева в определенном порядке, в зависимости от пункта (рис. 4.1.14 – 4.1.16). Конечно, вывод будет произведен, если дерево не пустое. Перед выводом исходное дерево было немного дополнено элементами (рис. 4.1.17).
Рисунок 4.1.14 – Прямой обход
Рисунок 4.1.15 – Обратный обход
Рисунок 4.1.16 - Симметричный обход
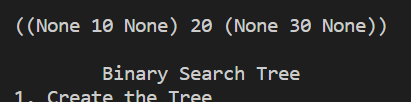
Рисунок 4.1.17 – Структура текущего бинарного дерева
Предпоследний, 12-ый пункт позволяет сгенерировать случайное дерево размером от 3 до 15 узлов с диапазоном значений [1; 100]. Если до этого имелось другое дерево, оно будет перезаписано.
Последний пункт меню позволяет пользователю прекратить работу с программой, и она корректно завершает свою работу.