Отчет по курсовой работе

2.1. Структурная схема исходной нескорректированной САУ в соответствии с табл.1.

Рис.1 Структурная схема исходной нескорректированной САУ

2.2. Дифференциальные уравнения в операторной форме записи в общем виде (на основании дифференциальных уравнений (1) – (4) и табл.2.

; (1.1)

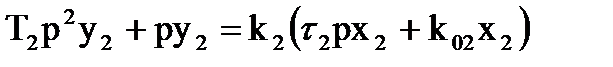; (2.1)

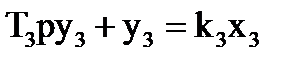; (3.1)

; (4.1)

2.3. Получение передаточных функций типовых звеньев структурной схемы.

Из (1.1): ;

- апериодическое звено

Из (2.1): ;

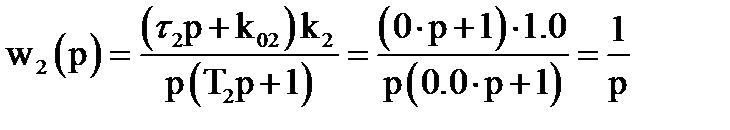- интегрирующее звено

Из (3.1): ;

- безынерционное звено

Из (4.1): ;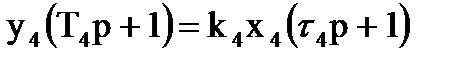

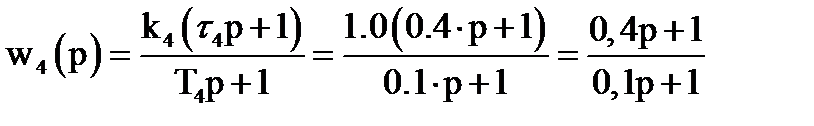- апериодическое звено

2.4. Определение передаточной функции САУ в разомкнутом состоянии.

Определим передаточную функцию системы в разомкнутом состоянии , выделив в ней коэффициент передачи разомкнутой системы .

Передаточная функция разомкнутой системы:

2.5. Передаточные функции замкнутой САУ по задающему v и возмущающему f воздействиям.

Передаточная функция замкнутой системы по управлению:

Рис.2 Схема набора структуры САУ по входному воздействию.

Рис.3 График переходных характеристик САУ по входному воздействию.

Так как графики функций совпадают, значит рассчитано верно.

Δy(∞)=1 - =0

Передаточная функция замкнутой системы по возмущению:

Рис.4 Схема набора структуры САУ по возмущающему воздействию.

Рис.5 График переходных характеристик САУ по возмущающему воздействию.

Так как графики функций совпадают, значит рассчитано верно.

Δy(∞)=1 - =1

2.6. Проверка условия устойчивости при помощи критерия Гурвица.

Для устойчивости линейной системы необходимо и достаточно, чтобы главный определитель матрицы Гурвица и все его n-1 миноры были положительными. Общий вид матрицы Гурвица:

В данном случае:

Необходимое и достаточное условие устойчивости выполняется.

2.7. Определение прямых показателей качества переходных процессов нескорректированной САУ по двум внешним воздействиям v и f методом цифрового моделирования.

Рис.6 Схема набора исходной структуры САУ в MatLab 2010.

Рис.7 График переходной характеристики при подаче входа и возмущающего воздействий.

Рис.8 Прямые показатели качества переходных процессов САУ при подаче входного и возмущающего воздействий.

Перерегулирование равно σ%=13.9%, а время регулирования t_p=1.64 c, установившееся значение равно 1.

3. Синтез последовательного корректирующего устройства на основании метода желаемой ЛАЧХ

3.1. Асимптотическая ЛАЧХ нескорректированной системы с использованием логарифмического масштаба

степень астатизма v=1, т.к. есть одно интегрирующее звено

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

РГЗ.2068956.40.06.13

Частоты сопряжения:

; ;

; ;

; ;

; ;

 

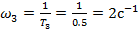3.2. Желаемая ЛАЧХ скорректированной САУ

Требуемый разомкнутый коэффициент передачи 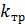скорректированной системы:

По номограмме Солодовникова, задавшись значением перерегулирования и временем регулирования , определив максимальное значение вещественной частотной характеристики находим частоту среза и необходимый запас устойчивости по модулю СЧ зоны , имеющий наклон -20дБ/дек.

3.3. ЛАЧХ последовательного корректирующего устройства:

; ; ;

; ; ;

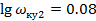; 2 ; ;

; ; ;

; ; ;

; ; ;

 

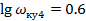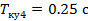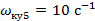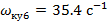С учетом численных значений:

Рис.9 Схема набора скорректированной структуры САУ в MatLab 2010.

 

Рис.10 Переходная характеристика САУ с корректирующим звеном с задающим и возмущающим воздействием.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

РГЗ.301037.000

Рис.11 Прямые показатели качества переходных процессов скорректированной САУ.

Перерегулирование равно σ%=11.4%, а время регулирования t_p=1.2 c, установившееся значение равно 1.

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

РГЗ.301037.000

Вывод: выполнили анализ нескорректированной непрерывной САУ. Данная САУ не отвечала требуемым показателям качества. Для того чтобы заданная САУ отвечала заданным параметрам качества был произведен синтез корректирующего устройства на основании метода желаемой ЛАЧХ. В конечном итоге, внедрили корректирующее устройство в данную САУ, что позволило достигнуть желаемых показателей качества.